感性电抗
Inductive Reactance
感性电抗是指电感线圈的电抗值随所加电压的频率变化而变化的特性,因为感性电抗与频率成正比。
感性电抗是电感线圈在交流电(AC)中抵抗电流变化的特性,它类似于直流电(DC)中电阻对电流的阻碍作用。
到目前为止,我们已经研究了电感器接入直流电源时的行为,并且希望此时我们已经知道,当在电感器两端施加直流电压时,其电流的增长并不是瞬时完成的,而是由电感器自感产生的反电动势(back emf)所决定的。
我们还看到,电感器中的电流会持续上升,直到经过 五个时间常数 后达到最大稳态值。流经电感线圈的最大电流仅受线圈绕组中电阻部分(以欧姆为单位)的限制,根据欧姆定律,这由电压与电流的比值 V / R 决定。
当在电感器两端施加交流电压时,电流的变化方式与直流情况下完全不同。正弦波电源会在电压和电流波形之间产生相位差。在交流电路中,线圈对电流的阻碍不仅取决于电感值,还取决于交流波形的频率。
在交流电路中,流经线圈的电流所受的阻碍由电路的交流电阻决定,这种交流电阻更常被称为阻抗(Impedance, Z)。由于“电阻”这个术语通常用于直流电路,因此为了区分直流电阻和交流电阻,交流电阻一般称为电抗(Reactance)。
和电阻一样,电抗的单位也是欧姆(Ω),但用大写字母 X 表示,以区别于纯电阻值。
对于我们关注的元件——电感器,它的电抗称为感性电抗(Inductive Reactance)。换句话说,电感器在交流电路中表现出的电气“电阻”就叫做感性电抗。
感性电抗的符号是 X_L,它是在交流电路中抵抗电流变化的特性。在之前关于交流电路中的电容的教程中,我们看到,在纯电容交流电路中,电流 I_C 超前电压 90°。而在纯电感交流电路中则恰好相反,电流 I_L 滞后施加电压 90°,即 \pi/2 \ \text{弧度}。
交流电感电路
AC Inductor Circuit
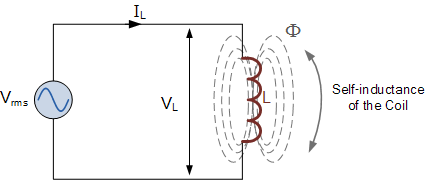
在上面所示的纯电感电路中,电感器直接连接在交流电源电压两端。由于电源电压会随频率的变化而周期性升高和降低,线圈中自感产生的反电动势(back emf)也会随之相应地升高和降低。
我们知道,这个自感电动势与流经线圈电流的变化率成正比,并且当电源电压从正半周跨越到负半周,或者从负半周跨越到正半周(即正弦波的 0° 和 180° 位置)时,自感电动势达到最大值。
相应地,当交流正弦波处于其最大值或最小值(即峰值电压位置)时,电压变化率最小。在这些位置,流经电感电路的电流达到最大值或最小值。这一规律在下图中有所显示。
交流电感器相量图
AC Inductor Phasor Diagram
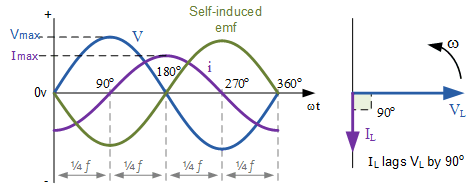
这些电压与电流波形表明,对于一个纯电感电路,电流相对于电压滞后 90^\circ。同样,我们也可以说电压相对于电流超前 90^\circ。无论哪种方式表述,一般的表达是电流滞后,如向量图所示。此处电流向量和电压向量相差 90^\circ,电流滞后电压。
我们还可以将此表述写为:
这里是相对于电压 V_L 来说的。
如果电压波形被认为是一个正弦波,那么电流 I_L 可以被认为是一个负的余弦波,我们可以定义任意时刻的电流值为:
其中, \omega 的单位是弧度每秒(rad/s),t 的单位是秒(s)。
由于在纯电感电路中电流总是滞后电压 90^\circ,我们可以通过知道电压的相位来确定电流的相位,反之亦然。因此,如果我们知道 V_L 的值,那么 I_L 必然滞后 90^\circ;同样,如果我们知道 I_L 的值,那么 V_L 必然超前 90^\circ。
那么,电感电路中电压与电流的这种比值会得到一个公式,该公式定义了线圈的感性电抗 X_L:
我们可以将上述感性电抗的公式改写为一个更常用的形式,使用电源的普通频率而不是以弧度表示的角频率:
其中, f 是频率, L 是线圈的电感量,且 2\pi f = \omega。
从上面的感性电抗公式可以看出,如果频率或电感值增大,那么整体的感性电抗值也会增大。当频率趋近无穷大时,电感的电抗也会增大到无穷大,表现得像一个开路。
然而,当频率趋近于零或直流(DC)时,电感的电抗会减小到零,表现得像一个短路。
因此,感性电抗与频率成正比。换句话说,感性电抗随频率增加而增加,这使得 X_L 在低频时较小,而在高频时较大。这在下图所示的感性电抗与频率的关系曲线上得到了体现。
Inductive Reactance against Frequency
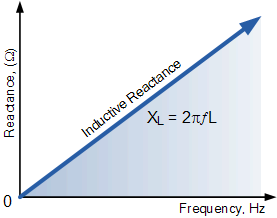
曲线的斜率表明,电感器的感性电抗会随着其两端所加电源频率的增加而增大。
因此,感性电抗与频率成正比,可表示为:
由此可见,在直流(DC)情况下,电感器的感性电抗为零(表现为短路);而在高频情况下,电感器的感性电抗趋于无穷大(表现为开路)。
感性电抗实例 1
一只电感量为 150\,\text{mH} 且无电阻的线圈,接在 100\,\text{V}、50\,\text{Hz} 的电源两端。求该线圈的感性电抗以及流经它的电流。
解:
感性电抗:
电流:
答案:
感性电抗 X_L = 47.12\,\Omega
电流 I = 2.12\,\text{A}
交流电源通过串联 LR 电路
AC Supply through an LR Series Circuit
到目前为止,我们考虑的是一个纯电感线圈,但实际上,不可能存在纯电感,因为所有的线圈、继电器或电磁铁,无论其电阻多么小,都会因线圈导线本身而具有一定的电阻。这样,我们就可以将一个简单的线圈看作是一个电阻与一个电感串联的组合。
在一个同时包含电感 L 和电阻 R 的交流电路中,总电压 V 将是两个分量电压 V_R 和 V_L 的相量和。这意味着,流经线圈的电流依然会滞后电压,但滞后角会小于 90^\circ,具体大小取决于 V_R 和 V_L 的值。
电压与电流之间新的相位角称为电路的相位角,用希腊字母 \Phi 表示。
为了画出电压与电流之间关系的向量图,需要找到一个参考量或公共分量。在串联 R–L 电路中,电流是公共量,因为同一电流流经每个元件。因此,这个参考量的相量通常从左到右水平绘制。
根据我们在电阻器和电容器教程中的内容,我们知道,在纯电阻交流电路中,电流与电压是同相的,因此 V_R 向量会按比例叠加在参考电流线上。
而根据上面的内容,我们也知道,在纯电感交流电路中,电流相对于电压是滞后的,因此 V_L 向量会相对于参考电流向量超前 90^\circ,并按与 V_R 相同的比例绘制。如下图所示:
串联 LR 交流电路
LR Series AC Circuit
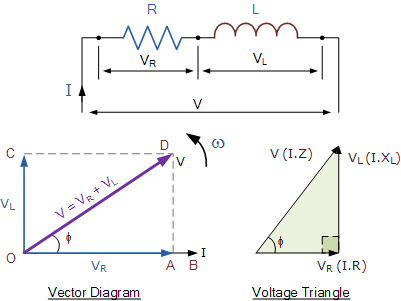
在上面的向量图中,可以看到 OB 线表示电流的参考线,OA 线表示电阻部分的电压,它与电流同相。OC 线表示感性电压,它相对于电流超前 90^\circ,因此可以看出电流相对于电压滞后 90^\circ。OD 线给出了电路中的合成电压或电源电压。
电压三角形可由勾股定理推导,公式为:
根据欧姆定律:
则:
因此,电流为:
在直流电路中,电压与电流的比值称为电阻。然而在交流电路中,这个比值称为阻抗(Impedance, Z),其单位同样为欧姆(Ω)。阻抗是在含有电阻与感性电抗的交流电路中对电流流动的总阻碍。
如果将上面电压三角形的各边都除以电流 I,就可以得到另一个三角形,其三边分别表示电阻、电抗和阻抗。这个新的三角形称为 阻抗三角形(Impedance Triangle)。
阻抗三角形
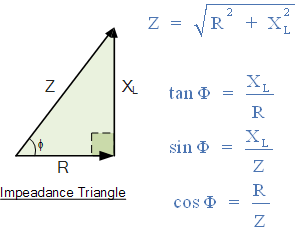
感性电抗实例 2
一个螺线管线圈的电阻为 30\,\Omega,电感量为 0.5\,\text{H}。若流经线圈的电流为 4\,\text{A},试计算:
a) 当频率为 50\,\text{Hz} 时的电源电压
首先计算感性电抗:
计算阻抗:
计算电源电压:
b) 电压与电流之间的相位角
最终答案:
电源电压 V = 640\,\text{V}
相位角 \Phi = 79.2^\circ(电流滞后电压)
交流电感器的功率三角形
Power Triangle of an AC Inductor
在感性电路中,还有另一种可以使用的三角形表示方式——功率三角形。
在感性电路中,功率称为无功功率(Reactive Power),其单位为乏(Var),符号为 Var,度量单位为伏安无功(volt-amps reactive)。在串联 RL 交流电路中,电流相对于电源电压滞后一个角度 \Phi。
在纯感性交流电路中,电流与电源电压完全相差 90^\circ。因此,线圈消耗的总无功功率为零,因为任何消耗的功率都会被自感反电动势产生的功率抵消。换句话说,在一个完整周期结束时,纯电感所消耗的净有功功率(瓦特)为零,因为能量既从电源吸收,又返回电源。
线圈的无功功率 Q 可表示为:
(形式上类似于直流电路中的 I^2 R 公式)。
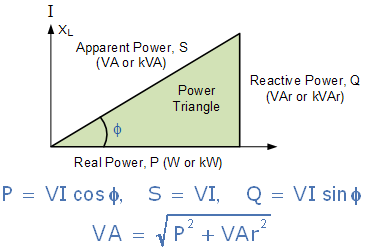
在交流电路的功率三角形中,三条边分别表示:
视在功率(Apparent Power, S)
有功功率(Real Power, P)
无功功率(Reactive Power, Q)
如图所示,功率三角形反映了三者的相互关系。
需要注意的是,实际的电感器或线圈由于绕组的电阻,会产生一定的功率消耗(以瓦特为单位),这是由其阻抗 Z 引起的。
附录
单词表
公式总结
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

