波形的峰值因数
Crest Factor of a Waveform
峰值因数通过峰值与均方根值的比值来描述波形的形状,对于纯正弦波,峰值因数等于 1.414。
峰值因数(Crest Factor,CF)是我们用来分析不同类型周期波形的另一种数学关系。峰值因数有时也称为峰值系数(Peak Factor)或幅值系数(Amplitude Factor),用于定义特定周期波形的质量,因为周期波形可以具有许多不同的形状。
波形的峰值因数非常重要,因为它可以指示施加到交流电路的最大电压。例如,电容器或电缆的绝缘击穿电压将取决于所用交流电压的最大电压。因此,任何交流元件都必须能够承受峰值电压,而不仅仅是所施加电压的均方根(RMS)值。
我们在电气和电子工程中使用的最常见的周期波形是正弦波。交流电压或电流的正弦波可以由其最大值、平均值和均方根值(RMS)来定义,如下所示。
正弦波形
Sinusoidal Waveform
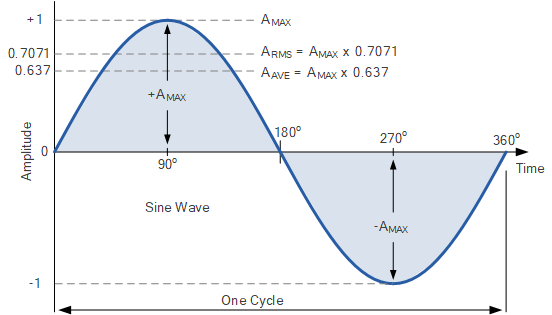
任何波形的最大幅度 A_{\max} 通常称为其峰值或最大值。对于任意正弦波,其最大正值(正峰值)在旋转角度 90^\circ 时达到;其最大负值(负峰值)在一个完整周期内的 270^\circ 时达到。因此,纯正弦波具有两个大小相等但方向相反的峰值,正峰值为 +A_{\max},负峰值为 -A_{\max}。
由于交流波形随时间周期性变化,因此不存在常数或稳态值。其等效的直流值(在电阻中产生相同 I^2R 发热效应的值)称为均方根值(Root-Mean-Square,RMS)。
交流波形的 RMS 值是对一个完整周期内波形进行计算的有效值,表示为:
由此可见,交流波形的最大峰值与 RMS 值之间存在直接关系,该比值即为峰值因数(Crest Factor)。因此,任何波形的峰值因数定义为:
基本峰值因数公式:
Basic Crest Factor Formula
纯正弦波的波峰因数定义为:
由此可见,峰值因数定义为周期波形的峰值与其均方根值的比值。因此,对于任何交流信号,包括方波,其峰值因数总是大于 1(单位);随着波形越尖峰,峰值因数也会增大。
注意,如果正弦波是完美正弦波,则无论峰值为何,其峰值因数始终等于 1.414(\sqrt{2})。
峰值因数示例 No.1
一个正弦波的最大峰值为 232 伏,计算其峰值因数。
峰值因数示例 No.2
一交流电压的最大峰值为 96 V,峰值因数为 1.5。计算其均方根值。
虽然上述解释假设波形为纯正弦波,但峰值因数仍然可以用于计算其他非正弦的重复周期波形,例如方波,因为频率、周期和峰值的含义相同。
这是因为方波也可以由基于基波的不同奇次谐波频率的无限多个正弦波叠加而成。
方波的峰值因数
Square Waveform Crest Factor
方形周期波可以归类为另一种周期波形,它在围绕接地中心的两个固定值之间瞬时交替。其最大值在时间上的持续时间与最小值的持续时间相等。因此,方波是占空比为 50%、时间周期相等的矩形波的特例,我们仍然可以求出它的峰值因数。
双极性方波
Square Wave (Bipolar) Waveform
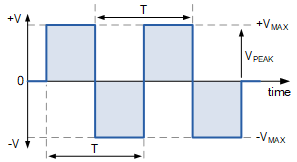
任何周期波形的直流平均值等于其在一个完整周期(T)内所有面积的平均值。但由于对称方波正半周的总面积恰好等于负半周的总面积,其净面积为零。也就是说,对称方波在一个完整周期内的平均值为零,因为负半周抵消了正半周。
然而,仅正半周或负半周单独的平均值并不为零。因此,我们可以仅对半周期计算方波的平均值,类似于正弦波。
对称方波正半周期的平均电压值 V_{\mathrm{ave}} 必须等于其峰值 V_{\max},因为在半周期内它实际表现为直流电压。因此:
注意,对于非对称波形(如半波整流电压),其平均值通常在一个完整周期内计算。
此外,由于对称方波的任意瞬时值始终等于其正峰值 +V_p 或负峰值 -V_p,该瞬时值的平方因此是常量 (V_p)^2。例如,在任意时刻取方波的瞬时值,其幅值总等于峰值,平方后即 (V_p)^2。
因此,为符合均方根定义,电压平方的平均值也为 V_p^2。对该平均值取平方根,即 \sqrt{V_p^2}=V_p。也就是说,对于对称方波,其峰值幅度与其 RMS 值完全相同:
因此,如果峰值(最大幅度)、平均值和 RMS 值都相同,那么对称方波的峰值因数(峰值与平均值之比)可以简单地表示为:
从这里我们可以看到,对于对称方波,其峰值因数等于 1.0(单位),由于扁平的方波形状使得峰值、平均值和平方值相同,因此我们期望其峰值因数为一。但对于诸如脉冲列之类的非对称方波,又该如何计算其峰值因数呢?
脉冲列的峰值因数
Pulse Train Crest Factor
周期性矩形脉冲序列的峰值因数按照占空比(Duty Cycle,也称标高比)来定义。如我们所知,完成一个完整周期所需的时间称为周期时间 T。
对于一系列脉冲(脉冲列),占空比是指通断时间 T_{\text{ON}} 在一个完整周期 (T_{\text{ON}} + T_{\text{OFF}})中的比例,通常以百分比表示。也就是说,占空比是脉冲宽度与周期之比:
占空比波形
Duty Cycle Waveform

例如,如果脉冲的导通时间为 12 ms,周期为 60 ms,则占空比为:
同理,若导通时间为 45 ms,则
也就是说,该脉冲在整个周期中有四分之三的时间处于“导通”状态。
显然,如果导通时间等于关断时间,即 T_{\mathrm{ON}} = T_{\mathrm{OFF}},那么占空比为 50%,对应于方波形状,因为
不同的 T_{\mathrm{ON}} 与 T_{\mathrm{OFF}} 比值会产生不等于 1 的标空比(Mark-to-Space Ratio)。脉冲列占空比的通用表达式为:
由于正弦波的峰值因数定义为峰值除以均方根值( Vp/Vrms),则对于占空比可变的脉冲列,其峰值因数可表示为:
由于脉冲列的幅度恒定,其峰值因数主要取决于其占空比。例如,假设占空比为 10%(0.1)、50%(0.5)和 90%(0.9),如下所示。
脉冲列峰值因数
10% 占空比时:
50% 占空比时:
90% 占空比时:
由此可见,随着脉冲列占空比从 10% 增加到 90%,其峰值因数从 3.0 降低到 0.33。这是因为在 10% 占空比时,脉冲列类似一系列尖锐的尖峰;而在 90% 占空比时,则非常接近平顶的恒定直流电源。
峰值因数总结
在本教程中,我们已经看到峰值因数(Crest Factor)是波形最大值或峰值与其均方根值之比。术语“峰值因数”描述了电气波形的形状或结构,提供了关于其特性以及它与完美正弦波相似程度的信息。显然,峰值因数越低越好,因为连接的负载从电力系统吸取功率的效率更高。
例如,电压峰值因数表示电路对电源的负载情况;电流峰值因数则表示负载从电源消耗电流的方式。换言之,峰值因数可用于显示连接的负载和/或无功元件如何影响电力供应网络的功率处理能力,因为高峰值因数会导致系统损耗增大。
正如我们所见,不同类型的电气波形根据其尖峰程度会有不同的峰值因数,波形越尖峰,峰值因数越高。对于对称方波,其峰值因数为“1”(单位),因为其 RMS 值与峰值相同,与计算其形状因数相同。对于纯正弦波,其峰值因数始终等于 1.414。
下表给出了上述不同种类波形的峰值因数公式及数值:
附录
单词表
峰值因数的实践意义
表 1 波峰因数在国家电网不同应用场景中的意义
表 2 常见应用场景的推荐波峰因数参考值
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

