Logo

Menu

张彤
张彤
Published on 2025-07-14 / 2 Visits
0
0

22.波形的形状因数

波形的形状因数

Form Factor of a Waveform

形状因数描述波形的形状或结构，是其均方根值与平均值之比。

波形形状因数（Form Factor，简称 F_F）是一种数学关系，用于分析不同类型的周期波形。形状因数是一种定义周期波形形态、结构甚至质量的方法。在其他情况下，形状因数也可用于度量含有大量谐波峰值的正弦波的“峰度”。

虽然“形状因数”这一术语对不同波形可能具有不同的含义，但它仍能为我们提供波形本身的良好图示表示，以及关于其电气特性和交流电源使用效率的有用信息。理解波形的形状因数在电气工程和信号处理领域同样重要，因为它有助于分析和设计电气电路及系统。特定周期波形的形状因数还能揭示其频率成分、谐波成分及其他特性，这些都是诸如整流器和基于电力的高压电路等各种电力应用所必需的。

因此，我们可以使用形状因数来定义某一波形相对于另一波形的尖锐程度或“峰度”。波形越尖锐，其形状因数越大；反之亦然。例如，方波的形状因数最低可达 1.0（即单位形状因数），但对于一些更尖锐的波形（如三角波），形状因数可能高达 3 或 4。

不同类型的电信号具有各自独特的形状因数，我们可以根据其标准波形形状对它们进行分类。

常见的形状因数包括：

  • 正弦波形状因数Sinusoidal Form Factor： 正弦波具有平滑、连续的振荡，以其频率、幅值和相位为特征。

  • 方波形状因数Square Form Factor： 方波具有恒定的幅值，在高电平和低电平之间突变。

  • 三角波形状因数Triangular Form Factor： 三角波呈线性上升和下降，在峰值和谷值之间呈三角形。

  • 锯齿波形状因数Sawtooth Form Factor： 锯齿波呈锯齿状，上升迅速、下降缓慢。

  • 脉冲波形状因数Pulse Form Factor： 脉冲波由不同宽度和幅值的脉冲组成。

以上即为几种常见周期波形的形状因数及其特点。

波形周期分类

Types of Periodic Waveform

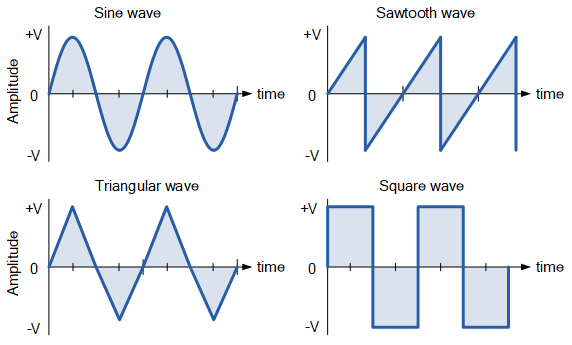
我们在电气和电子工程中使用的最常见的周期波形是正弦波（或它的变体，如余弦波）。交流正弦电压或电流波形可以通过其最大值、平均值和均方根值（RMS）来定义，如下所示。

Sinusoidal Waveform

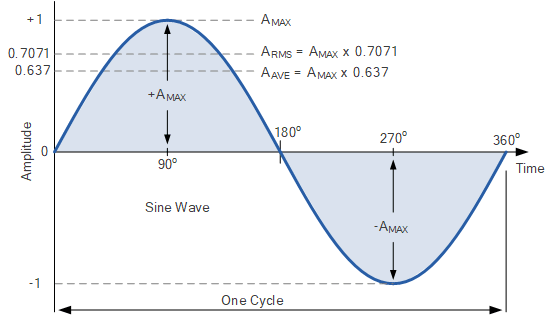
波形的最大振幅称为其峰值或最大值，其中波形的最大正值 （+A_{\mathrm{max}}）称为正峰值，最大负值 （–A_{\mathrm{max}}）称为负峰值。

最大正值与最大负值之差通常称为波形的峰峰值。因此，由于正弦波在其峰值处始终对称，峰峰peak-to-peak值永远是峰值的两倍，即： 2A_{\mathrm{max}}。

正弦波的数学平均值取自半个周期，即 0 到 \pi。之所以取半周期，是因为在一个完整周期（0 到 2\pi）内，正弦波的正、负部分相等且相反，其平均值为零。对于正弦波，其平均值（或称算术平均值）为：

A_{\mathrm{AVE}} = \frac{2 \times A_{\mathrm{max}}}{\pi} = \frac{2}{\pi} A_{\mathrm{max}} \approx 0.637 \, A_{\mathrm{max}}


交流波形的均方根值（RMS，Root-Mean-Square）是其等效值，即产生相同热效应的直流值。正弦波的 RMS 值取自一个完整周期，计算公式为：

A_{\mathrm{RMS}} = \frac{A_{\mathrm{max}}}{\sqrt{2}} = \frac{1}{\sqrt{2}} A_{\mathrm{max}} \approx 0.7071 \, A_{\mathrm{max}}


因此，交流波形的峰值、平均值和 RMS 值之间存在明确的关系，可分别用形状因数（Form Factor）或峰值因数（Crest Factor）来表达。任何波形的形状因数定义为：

基本形状因数公式

Basic Form Factor Formula

Form \ Factor = \frac{RMS \ Value}{Average Value}


对于一个纯正弦波而言，形状因数如下:

F_F = \frac{\text{RMS 值}}{\text{平均值}} = \frac{\tfrac{1}{\sqrt{2}}\,A_{\max}}{\tfrac{2\,A_{\max}}{\pi}} = \frac{0.7071\,A_{\max}}{0.637\,A_{\max}} = \frac{\pi}{2\sqrt{2}} = 1.11


那么，形状因数定义为有效值与平均值之比。如果正弦波是一个理想的正弦波，那么其形状因数与峰值无关，将始终等于 1.11。因此，默认情况下，理想正弦波的形状因数永远不会高于或低于 1.11。

形状因数例题 No.1

一个正弦波的最大峰值为 270 伏特。计算其形状因数。

F_F = \frac{V_{\mathrm{RMS}}}{V_{\mathrm{AVE}}} = \frac{0.7071 \times V_{\max}}{0.637 \times V_{\max}} = \frac{0.7071 \times 270}{0.637 \times 270} = \frac{191}{172} = 1.11

那么，形状因数定义为有效值与平均值之比。如果正弦波是一个理想的正弦波，那么其形状因数无论峰值大小都始终等于 1.11。因此，默认情况下，理想正弦波的形状因数永远不会高于或低于 1.11。

形状因数例题 No.2

一个交流电压的平均值为 160 伏特，形状因数为 1.25。计算它的均方根值和最大峰值。

  1. 正弦电压的均方根值

    F_F = \frac{V_{\mathrm{RMS}}}{V_{\mathrm{AVE}}} \\ \quad\therefore\quad V_{\mathrm{RMS}} = F_F \times V_{\mathrm{AVE}} = 1.25 \times 160 = 200\ \mathrm{V}

  2. 正弦电压的最大峰值

    V_{\max} = \sqrt{2}\,V_{\mathrm{RMS}} = 1.414 \times 200 = 282.8\ \mathrm{V}

虽然以上解释假设波形是纯正弦波，但形状因数仍可用于计算其他非正弦波形，例如二极管整流所产生的波形。

单相半波整流波形

Single-phase Half-wave Rectified Waveforms

由于半波整流器在其设计中只使用一个功率二极管，因此它们仅通过输入交流电源的一半，如下所示。

半波整流波形

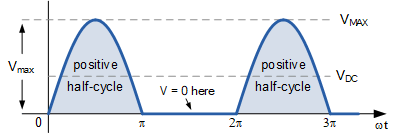
对于半波整流的正弦电压，其直流平均电压 V_{\mathrm{DC}} 定义为： V_{\mathrm{DC}} = \frac{V_{\max}}{\pi} = 0.318\,V_{\max},而有效均方根电压 V_{\mathrm{RMS}} 定义为： V_{\mathrm{RMS}} = \frac{V_{\max}}{2}.因此，半波整流输出的形状因数为：

F_{F(\mathrm{HW})} = \frac{V_{\mathrm{RMS}}}{V_{\mathrm{DC}}} = \frac{\tfrac{V_{\max}}{2}}{\tfrac{V_{\max}}{\pi}} = \frac{\pi}{2} \approx 1.57

由此可见，对于由纯正弦电源供电的单相半波整流器，其形状因数计算为 1.57。

单相全波整流波形

Single-phase Full-wave Rectified Waveforms

全波整流器——无论是中点抽头、双向还是桥式配置——都利用输入正弦电源的两个半周，如下所示。

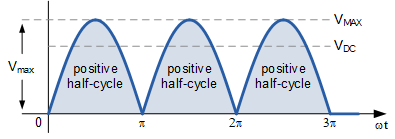
对于全波整流的正弦电压，其平均直流电压 V_{DC} 将会是前面半波整流器值的两倍，因为它利用了整个正弦波的两个半周波，从而使得负载电流在这两个半周波中均按相同方向流动。

因此，V_{DC} 定义为：V_{DC} = \frac{2V_{MAX}}{\pi}，即 0.637\,V_{MAX}，而有效均方根电压 V_{RMS} 仍然为：V_{RMS} = \frac{V_{MAX}}{\sqrt{2}}，那么，全波整流的整形因数（Form Factor）为：

F_{\mathrm{FW}} \;=\;\frac{V_{\mathrm{RMS}}}{V_{\mathrm{DC}}} \;=\;\frac{\displaystyle\frac{V_{\max}}{\sqrt{2}}}{\displaystyle\frac{2V_{\max}}{\pi}} \;=\;\frac{\pi}{2\sqrt{2}} \;\approx\;1.11


正如我们所见，单相全波整流器计算得到的整形因数 1.11 与前面的正弦波相同。这是可以预期的，因为平均直流值 0.637 是在半个周期内计算得到的，而有效值（均方根）0.7071 是根据峰值 V_{MAX} 计算得到的。

  • 这里的“直流值”（V_{DC}）并不是指把三角波当成直流信号去算，而是指对波形取绝对值后（或只取正半周）的平均值，也就是波形的“直流分量”或“平均幅值”

三角波形整形因数

Triangular Waveform

除了正弦波形外，整形因数也可应用于其他类型的周期性非正弦波形，例如三角波形。顾名思义，三角波形由等斜率的正向和负向线性斜坡组成，先从零上升到正峰值，然后下降到负峰值，完成一个完整周期。三角波形的周期按峰到峰测量，如下所示。

三角波形

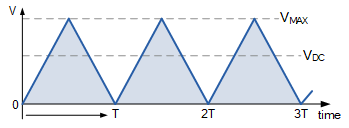
三角波形可以通过将标准 RC 振荡器与积分器级联来产生。所产生的方波在 +V_{MAX} 和 -V_{MAX} 之间摆动。显然，正峰值与负峰值之间的差值就是峰-峰值。

由于三角波形是对称的，三角电压（或电流）的有效值 V_{RMS} 为： V_{RMS} = \frac{V_{MAX}}{\sqrt{3}}，因为一个完整周期的形状是等腰三角形，每个半周期三角波形的平均值或直流值 V_{DC} 为： V_{DC} = \frac{V_{MAX}}{2}，那么三角波形的整形因数（Form Factor）为：

F_F = \frac{V_{RMS}}{V_{DC}} = \frac{\displaystyle\frac{V_{MAX}}{\sqrt{3}}} {\displaystyle\frac{V_{MAX}}{2}} = \frac{2}{\sqrt{3}} \approx 1.155


那么，对称三角波的形状因数被计算为：1.155，这意味着它比之前的圆滑正弦波更尖锐。

锯齿波形的形状因数

Sawtoothed Waveform Form Factor

锯齿波形是前面三角波的一种变体，其名称来源于锯齿波形酷似锯片齿的形状。

通常，在一个周期 T 内，它以恒定且直线的斜率从零上升到峰值 V_{MAX}，然后在一个周期结束时迅速下降到起始点零（或某个负值）。锯齿波形也称为斜坡波形，因为从零到最大值的上升部分与线性斜坡相同。

锯齿波形

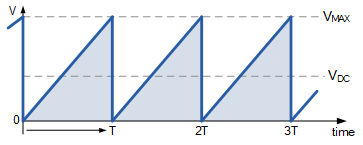
由于锯齿波电压上升呈线性增加，因此可以将其视为一系列直角三角形。由此其正向平均值或等效直流值仅为 V_{MAX}/2，与三角波相同。

由于锯齿波形对称且重复，其有效值（均方根值） V_{RMS} 因此为 V_{MAX}/\sqrt{3}。

那么，锯齿波的形状因数（Form Factor）为：

F_F = \frac{V_{RMS}}{V_{DC}} = \frac{\displaystyle\frac{V_{MAX}}{\sqrt{3}}}{\displaystyle\frac{V_{MAX}}{2}} = \frac{2}{\sqrt{3}} \approx 1.155


如我们所见，对于锯齿波形计算出的整形因数 1.155 与前面的三角波形完全相同，因为它们本质上都是一系列斜率由 V_{MAX}/T 定义的三角形。请注意，锯齿波形可以具有正向和负向的斜坡。

方波和脉冲波形

Square Wave Waveform

最后，让我们来看一下方波序列和脉冲波形的整形因数，这些都可被归类为一种周期性波形。对于方波和矩形脉冲波形，频率和周期的含义与最大值或峰值相同，因为它们在两个恒定电压水平之间切换，如下所示。

方波波形

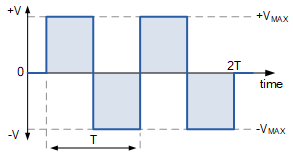
由于任何周期性波形的平均直流值等于其在正半周期（0 到 T/2 即 \pi）范围内的平均值 V_{AVE}。因此，方波的平均值等于其最大值 V_{MAX}，因为其在一个完整周期 T（2\pi）上的平均值为零。于是

V_{AVE} = V_{MAX}.


此外，方波的瞬时值始终等于其正最大值 +V_{MAX} 或负最大值 -V_{MAX}。因此其最大电压平方值为 V_{MAX}^2，其平方根即为 V_{MAX}。所以方波的均方根值

V_{RMS} = V_{MAX}.


由于最大幅值与均方根幅值相同，对称方波的整形因数（Form Factor）为：

F_F = \frac{V_{RMS}}{V_{DC}} = \frac{V_{MAX}}{V_{MAX}} = 1.


这样我们可以看到，对于对称方波，其整形因数等于“1.0”（单位整形因数）。由于方波具有平顶的最大值或峰值且无“尖峰性”，因此我们预期这里会出现单位整形因数。

周期性矩形脉冲序列的整形因数将取决于其占空比，也称为标空比。振幅为 V_{\mathrm{MAX}}、周期为 T 的脉冲波通常具有 50% 的占空比，即其标空比 T_{\mathrm{ON}}/T_{\mathrm{OFF}} 为 50:50 或 1。不同的 T_{\mathrm{ON}} 和 T_{\mathrm{OFF}} 持续时间将导致非单位的标空比。

对于称为脉冲列（pulse train）的脉冲序列，每个脉冲的宽度为 T_{\mathrm{ON}}，脉冲之间的间隔为 T_{\mathrm{OFF}}。由此我们可以看到，脉冲列具有周期： T = T_{\mathrm{ON}} + T_{\mathrm{OFF}}，如图所示。

正脉冲波形

Positive Pulse Waveform

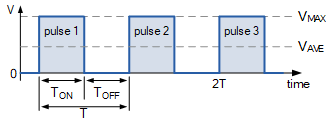
如果脉冲列的标空比为 unity，即 T_{\text{ON}}=T_{\text{OFF}}，那么平均电压值 V_{\text{AVE}} 将等于脉冲最大值的一半。也就是说：

V_{\text{AVE}} = \frac{V_{\max}}{2}.

显然，对于其它标空比，稳态输出将大于或小于 \tfrac{V_{\max}}{2}，取决于 T_{\text{ON}} 与 T_{\text{OFF}} 的具体比值。

因此，我们可以将 V_{\text{AVE}} 定义为：

V_{\text{AVE}} = V_{\max}\,\frac{T_{\text{ON}}}{T},

其中 \tfrac{T_{\text{ON}}}{T} 称为“占空比”（Duty Cycle，DC）。

始终为正的矩形脉冲的均方根等效值 V_{\text{RMS}} 来源于占空比的均方根值。也就是说，RMS 值等于其最大值乘以占空比的平方根：

V_{\text{RMS}} = V_{\max}\,\sqrt{\frac{T_{\text{ON}}}{T}}.


显然，在幅值恒定 V_{\max} 时，脉冲列的标空比会对脉冲的整形因数产生显著影响。我们可以取标空比分别为 10%（1:10）、50%（5:10）和 90%（9:10），且 V_{\max}=1 V 来演示这一点，如下所示：

在 10% 占空比时：

F_F = \frac{V_{\mathrm{RMS}}}{V_{\mathrm{DC}}} = \frac{V_{\max}\,\sqrt{\frac{T_{\mathrm{ON}}}{T}}} {V_{\max}\,\frac{T_{\mathrm{ON}}}{T}} = \frac{\sqrt{\frac{1}{10}}}{\frac{1}{10}} = \frac{0.316}{0.1} = 3.16

在 50% 占空比时：

F_F = \frac{V_{\mathrm{RMS}}}{V_{\mathrm{DC}}} = \frac{V_{\max}\,\sqrt{\frac{T_{\mathrm{ON}}}{T}}} {V_{\max}\,\frac{T_{\mathrm{ON}}}{T}} = \frac{\sqrt{\frac{5}{10}}}{\frac{5}{10}} = \frac{0.7071}{0.5} = 1.414

在 90% 占空比时：

F_F = \frac{V_{\mathrm{RMS}}}{V_{\mathrm{DC}}} = \frac{V_{\max}\,\sqrt{\frac{T_{\mathrm{ON}}}{T}}} {V_{\max}\,\frac{T_{\mathrm{ON}}}{T}} = \frac{\sqrt{\frac{9}{10}}}{\frac{9}{10}} = \frac{0.95}{0.9} = 1.06

由此可见，当脉冲列的占空比从 10% 增加到 90% 时，其形状因数从 3 以上降低到接近 1.0 （单位形状因数）。这是因为当占空比为 10% 时，脉冲类似于一个非常尖锐的尖峰；而当占空比为 90% 时，则非常接近期顶平坦的恒定电源。

整形因数教程总结

我们已经看到，整形因数是波形的有效值（RMS 值）与其平均直流值之比。“整形因数”一词反映了电气波形的形状或结构，提供了关于其特性以及波形与理想正弦波相似程度的信息。不同类型的电信号具有不同的整形因数，可根据其波形进行分类。

波形的整形因数最低可为 “1” （单位整形因数），对于较尖锐的脉冲状波形，可高达 3 或 4。整形因数为 1 意味着该波形的有效值（RMS 值）等于其最大（峰值）幅度。

下表给出了上述各类波形的整形因数公式及数值：

波形类型

整形因数公式

数值

正弦波

\displaystyle\frac{\pi}{2\sqrt2}

1.11

半波整流正弦波

\displaystyle\frac{\pi}{2}

1.57

全波整流正弦波

\displaystyle\frac{\pi}{2\sqrt2}

1.11

三角波

\displaystyle\frac{2}{\sqrt3}

1.155

锯齿波

\displaystyle\frac{2}{\sqrt3}

1.155

对称方波

1

1.0

50% 占空比脉冲波

\displaystyle\frac{V_{\max}\sqrt{\text{Duty Cycle}}}{V_{\max}\times\text{Duty Cycle}}

1.414

附录

三角波形的数学推导

1. 定义波形

周期为 T 的对称三角波，其在一个循环中可分为两个相同的半周期。取半周期 0 \le t \le \tfrac{T}{2} 内，电压线性上升，由

v(t) = \frac{2V_{\max}}{T}\,t

描述；另一个半周期对称下降。

2. 有效值 V_{RMS} 推导

\begin{aligned} V_{RMS}^2 &= \frac{1}{T} \int_0^T [v(t)]^2 \,\mathrm{d}t = \frac{2}{T} \int_0^{\frac{T}{2}} \Bigl(\frac{2V_{\max}}{T}t\Bigr)^2 \,\mathrm{d}t \\[6pt] &= \frac{2}{T}\,\frac{4V_{\max}^2}{T^2} \int_0^{\frac{T}{2}} t^2 \,\mathrm{d}t = \frac{8V_{\max}^2}{T^3} \left[\frac{t^3}{3}\right]_0^{\frac{T}{2}} \\[6pt] &= \frac{8V_{\max}^2}{T^3} \cdot \frac{\bigl(\tfrac{T}{2}\bigr)^3}{3} = \frac{8V_{\max}^2}{T^3} \cdot \frac{T^3}{8\cdot3} = \frac{V_{\max}^2}{3}. \end{aligned}

因此

V_{RMS} = \sqrt{\frac{V_{\max}^2}{3}} = \frac{V_{\max}}{\sqrt3}.


3. 平均值 V_{DC} 推导

\begin{aligned} V_{DC} &= \frac{1}{T}\int_0^T |v(t)|\,\mathrm{d}t = \frac{2}{T}\int_0^{\frac{T}{2}} v(t)\,\mathrm{d}t \\[6pt] &= \frac{2}{T} \int_0^{\frac{T}{2}} \frac{2V_{\max}}{T}\,t \,\mathrm{d}t = \frac{4V_{\max}}{T^2} \left[\frac{t^2}{2}\right]_0^{\frac{T}{2}} \\[6pt] &= \frac{4V_{\max}}{T^2} \cdot \frac{\bigl(\tfrac{T}{2}\bigr)^2}{2} = \frac{4V_{\max}}{T^2} \cdot \frac{T^2}{8} = \frac{V_{\max}}{2}. \end{aligned}


4. 三角波形的整形因数

\mathrm{Form\ Factor} = \frac{V_{RMS}}{V_{DC}} = \frac{\displaystyle\frac{V_{\max}}{\sqrt3}} {\displaystyle\frac{V_{\max}}{2}} = \frac{2}{\sqrt3} \approx 1.155.

波形因数的影响因素

下表将上述影响波形因数的主要因素及其作用简要整理：

主要因素

具体影响

波形形状

不同波形（正弦／方波／三角波／锯齿波／脉冲）固有的几何形状决定 V_{RMS} 与 V_{DC} 比例。

占空比（Duty Cycle）

脉冲类波形占空比越小，波形越尖峰， V_{DC}\propto\text{占空比} 下降快于 V_{RMS}\propto\sqrt{\text{占空比}}，形状因数增大。

谐波失真

非线性负载（整流器、变频器等）引入高次谐波，提升 V_{RMS} 相对 V_{DC} 的比值；滤波装置可降低谐波、减少形状因数。

直流分量

波形若含直流分量， V_{DC} 提升， V_{RMS} 同时变化，两者比值（形状因数）会随直流分量大小而增减。

对称性／整流方式

半波整流失去一半能量，降低平均值、增大形状因数；全波整流恢复对称后形状因数下降。

滤波与补偿

无源／有源滤波器、无功补偿平滑波形尖峰，降低高频分量对 V_{RMS} 的贡献，从而调整形状因数。

测量系统特性

仪表带宽、采样率不足或接线不当易“平滑”尖峰，导致测得 V_{RMS} 与 V_{DC} 偏差，影响形状因数计算。

温度与器件老化

变压器、电缆、滤波元件寄生参数随温度和老化变化，可能引起微弱波形失真，轻微影响形状因数。

单词表

英文术语

中文释义

full-wave

全波

half-wave

半波

rectified

整流

sinusoidal

正弦的

voltage

电压

average

平均值

DC

直流

VDC

直流电压（符号）

VMAX

峰值电压（符号）

RMS

均方根

VRMS

有效电压（符号）

form factor

整形因数

rectifier

整流器

half-cycle

半周期

load current

负载电流

effective

有效的

triangular

三角形的

waveform

波形

RC oscillator

RC 振荡器

integrator

积分器

rectangular

矩形的

sawtooth

锯齿状的

ramp

斜坡

symmetrical

对称的

isosceles

等腰的

equilateral

等边的

triangle

三角形

peak-to-peak

峰-峰值

period

周期

unity

单位（1.0）

square wave

方波

pulse waveform

脉冲波形

pulse train

脉冲列

duty cycle

占空比

mark-space ratio

标空比

TON

导通时间

TOFF

关断时间

crest factor

峰值因数

THD

总谐波失真

harmonics

谐波

non-linear load

非线性负载

Active Power Filter (APF)

有源滤波器

LC filter

LC 滤波器

Power Quality Analyzer

电能质量分析仪

True-RMS oscilloscope

真有效值示波器

IEC

国际电工委员会

IEEE

电气电子工程师学会

Q/GDW 651-2011

《电能质量评估技术导则》标准号

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途

21.阻抗与复阻抗
23.波形的峰值因数

Comment