Logo

Menu

张彤
张彤
Published on 2025-07-14 / 2 Visits
0
0

21.阻抗与复阻抗

阻抗与复阻抗

阻抗是在交流电路中对交流电流流动的总阻碍，并以欧姆表示。

在交流电路（常称为“AC 电路”）中，阻抗是对电流在电路中流动的阻碍。阻抗以欧姆为单位，表示电路中各种限流元件（如电阻 R、电感 L 和电容 C）综合作用的结果。

在直流电路（DC 电路）中，对电流流动的阻碍称为电阻；而在交流电路中，阻抗则既包括电路的电阻分量 R，也包括其无功分量 X。在直流电路里，电阻用字母 R 表示；而在交流电路中，用字母或符号 Z 来表示对电流流动的总阻碍。

同直流电阻一样，阻抗也是以欧姆为单位表达，在需要时也可使用欧姆的倍数和分数单位。例如微欧（μΩ 或 10⁻⁶ Ω）、毫欧（mΩ 或 10⁻³ Ω）、千欧（kΩ 或 10³ Ω）、兆欧（MΩ 或 10⁶ Ω）等。在每种情况下，都可以用欧姆定律来描述：

Z = \frac{V}{I},\quad I = \frac{V}{Z},\quad V = I \times Z

其中： Z 以欧姆为单位， V 以伏特为单位， I 以安培为单位。

阻抗形式 如前所述，阻抗 Z 是电路中电阻 R 与无功电抗 X 总值的综合；但阻抗还依赖于频率，因此它具有一个相位角。电抗的相位角（无论是感性还是容性）总是与电阻分量相差 90^\circ，因此电阻值和电抗值不能简单地算术相加来得到阻抗，也就是说 R + X \neq Z。

值得注意的是，纯电阻（不包括绕线电阻）不会随频率变化，因此没有电抗，其电阻值就等于阻抗值 (R = Z)。因此，电阻没有相位角，其两端的电压和通过的电流始终“同相”。

然而，感抗 X_L 或容抗 X_C 会随频率变化，导致电路的阻抗值随着供电频率的改变而变化。正因为如此，在交流电路分析中，有时会将电阻器的阻抗称为“阻性阻抗”，将电感和电容的阻抗称为“无功阻抗”。

由于电阻分量和无功分量之间相差 90^\circ，它们不能相加得到总阻抗，所以我们可以将这两个值分别在二维坐标系中绘出：横轴为电阻或“实轴”，纵轴为电抗或“虚轴”。这与构造直角三角形的方法相同。

下图中的直角三角形示意了电阻值与电抗值如何结合，三角形的斜边（最长边）即代表电路的复阻抗。

电阻与感性电抗

Resistance and Inductive Reactance

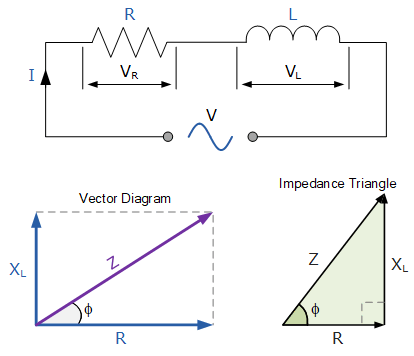
由于我们实际上处理的是一个三边的直角三角形，因此可以使用毕达哥拉斯定理及其相关方程，将表示电阻和感抗的直角三角形的两条直角边，与第三条斜边（即阻抗）的长度联系起来。毕达哥拉斯定理在阻抗、电阻和电抗方面的表达为：

Z^2 = R^2 + X^2

也就是说：

(\text{阻抗})^2 = (\text{电阻})^2 + (\text{电抗})^2

通过这种方式，我们可以表明Z是电阻向量 R 与感抗向量 X_L 的向量和，如图所示具有正斜率。

RL电路的阻抗

Impedance of an RL Circuit

R = R \\ X_L = 2\pi f L \\ Z^2 = R^2 + X_L^2 \\ Z = \sqrt{R^2 + X_L^2}


相角 (\phi) 定义为下图所示，两向量之间的角度（以度为单位）。

RL 电路的相角

Phase Angle of an RL Circuit

\begin{alignedat}{2} \tan\phi &= \frac{X}{R} = \frac{X_L}{R} &\quad&\Rightarrow \phi = \tan^{-1}\!\Bigl(\frac{X_L}{R}\Bigr), \\[6pt] \sin\phi &= \frac{X}{Z} = \frac{X_L}{Z} &\quad&\Rightarrow \phi = \sin^{-1}\!\Bigl(\frac{X_L}{Z}\Bigr), \\[6pt] \cos\phi &= \frac{R}{Z} &\quad&\Rightarrow \phi = \cos^{-1}\!\Bigl(\frac{R}{Z}\Bigr). \end{alignedat}


与先前包含电感和感性电抗的电路类似，我们也可以展示含有电容器和容性电抗的交流电路的复阻抗。

相同的直角图可用于展示电阻和容性电抗如何结合，其中三角形的斜边（最长边）表示电路的复阻抗。

请记住，对于电容器， Z 是电阻向量 R 和电抗向量 X_C 的矢量和。它沿与先前 X_L 向量相反的方向绘制，呈负斜率。这表明容性电抗对交流电路的影响与感性电抗相反。

电阻和容性电抗

Resistance and Capacitive Reactance

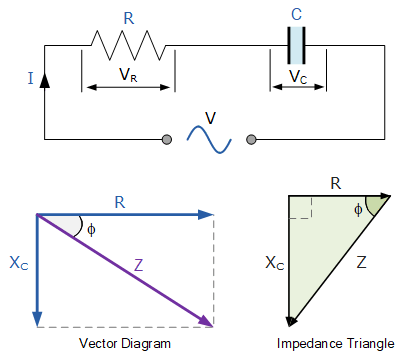
再次使用毕达哥拉斯定理及其相关方程，我们可以将表示电阻和容性电抗的直角三角形的两条直角边，与斜边（即复阻抗）的长度联系起来。毕达哥拉斯定理在阻抗、电阻和电抗方面的表达为：

RC 电路的阻抗

Impedance of an RC Circuit

\begin{aligned} R &= R, \\[6pt] X_C &= \frac{1}{2\pi f C}, \\[6pt] Z^2 &= R^2 + X_C^2, \\[6pt] Z &= \sqrt{R^2 + X_C^2}. \end{aligned}


相角 \phi 的正切定义了阻抗矢量与电阻矢量之间的夹角（以度为单位）。相角等于电抗与电阻之比，如下所示：

RC电路的相角

Phase Angle of an RC Circuit

\begin{alignedat}{2} \tan\phi &= \frac{X}{R} = \frac{X_C}{R} &\quad&\Rightarrow \phi = \tan^{-1}\!\Bigl(\frac{X_C}{R}\Bigr), \\[6pt] \sin\phi &= \frac{X}{Z} = \frac{X_C}{Z} &\quad&\Rightarrow \phi = \sin^{-1}\!\Bigl(\frac{X_C}{Z}\Bigr), \\[6pt] \cos\phi &= \frac{R}{Z} &\quad&\Rightarrow \phi = \cos^{-1}\!\Bigl(\frac{R}{Z}\Bigr). \end{alignedat}


因此，可以使用向量图来显示电阻和电抗（感性和容性）如何组合形成阻抗。我们还可以注意到，可以使用电路的欧姆值——无论是 Z、 R 还是 X——来求出电源电压 V_S 与电路电流 I 之间的相位角 \phi。

阻抗例题 No. 1

一个 53 mH 的电感和一个 15 Ω 的电阻串联连接。计算在 60 Hz 时的总阻抗和相位角。

  1. 电路总阻抗 Z：

    \begin{aligned} R &= 15\,\Omega, \\[6pt] X_L &= 2\pi f L = 2 \times \pi \times 60 \times 53 \times 10^{-3} = 20\,\Omega, \\[6pt] Z &= \sqrt{R^2 + X_L^2} = \sqrt{15^2 + 20^2} = 25\,\Omega. \end{aligned}

  2. 相位角, \theta:

    \tan\phi = \frac{X_L}{R} \quad\Rightarrow\quad \phi = \tan^{-1}\!\Bigl(\frac{20}{15}\Bigr) = 53.1^\circ.

阻抗例题 No.2

用万用表测量，发现一个螺线管线圈的静态电阻为 12 Ω。当该线圈接入一个 100 V、1000 Hz 的电源时，电流为 5 A。计算该线圈的电感量和功率因数。

  1. 线圈的感性电抗 X_L：

    电流 I：

    I = \frac{V}{Z} \\ \quad\therefore\quad Z = \frac{V}{I} = \frac{100}{5} = 20\,\Omega


    阻抗平方关系：

    Z^2 = R^2 + X_L^2 \\ \quad\therefore\quad X_L^2 = Z^2 - R^2


    感性电抗 X_L：

    X_L = \sqrt{Z^2 - R^2} = \sqrt{20^2 - 12^2} = 16\,\Omega


    电感量 L：

    X_L = 2\pi f L \\ \quad\therefore\quad L = \frac{X_L}{2\pi f} = \frac{16}{2\pi \times 1000} = 2.5\,\mathrm{mH}

  2. 功率因数:

    \cos\phi = \frac{R}{Z} = \frac{12}{\sqrt{12^2 + 16^2}} = \frac{12}{20} = 0.6

我们已经看到，阻抗 Z 是交流电路中电阻 R 与电抗 X 的综合作用，而纯电抗分量 X 与电阻分量相位相差 90^\circ，感性电抗为 +90^\circ，容性电抗为 -90^\circ。

但如果一个串联交流电路同时包含感性电抗 X_L 和容性电抗 X_C，这将如何影响电路的复阻抗？

RLC 电路的阻抗

电抗就是电抗！虽然电感的阻抗三角图呈正斜率，电容的阻抗三角图呈负斜率，但将两者在数学上相加会得到电路的整体阻抗值。

串联电路的等效电抗是感性电抗 X_L 与容性电抗 X_C 的向量和，如下所示：

X = X_L + (-X_C) = X_L - X_C

从而得到

Z^2 = R^2 + X^2 = R^2 + \bigl(X_L - X_C\bigr)^2 \\ Z = \sqrt{R^2 + X^2} = \sqrt{R^2 + \bigl(X_L - X_C\bigr)^2}

作为一般经验法则，我们应当用较大电抗值减去较小电抗值，无论是 X_L 还是 X_C，结果都相同。这是因为在数学上，对负数取平方必然得到正值。例如， (-2)^2 与 2^2 的结果都是 +4。

因此，在将电抗值与电阻值相加之前，使用 (X_L - X_C) 或 (X_C - X_L) 来求电路的等效电抗都是正确的。

换言之，就是容抗和阻抗相减的绝对值

所得的阻抗三角形如下：

RLC 阻抗三角形

RLC Impedance Triangle

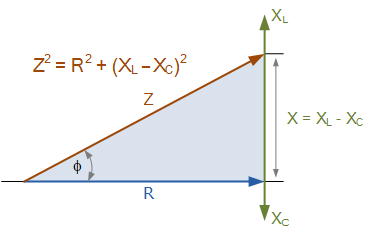
随着阻抗斜率的方向取决于哪种电抗更大——感性电抗 （X_L - X_C）或容性电抗 （X_C - X_L），因此电路的复阻抗可表示为：

Z = R \pm jX

显而易见，如果一个交流电路仅串联了电感和电容，则阻抗为

Z = X_L - X_C

或者反之亦可。当电路处于谐振状态时，由于 X_L = X_C，净电抗为零，所以

Z = 0


这就是为什么在串联谐振电路中，电流仅受有功电阻 R 限制的原因。

阻抗例题 No.3

一个非感性电阻 10\ \Omega、一个电容 100\,\mu\mathrm{F} 和一个电感 0.15\,\mathrm{H} 串联接入 240\,\mathrm{V}、50\,\mathrm{Hz} 电源。计算该电路的感性电抗、容性电抗、复阻抗及功率因数。

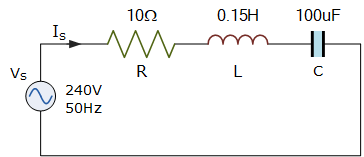
  1. 感性电抗 X_L：

    X_L = 2\pi fL = 2\pi \times 50\,\text{Hz} \times 0.15\,\text{H} = 47.1\,\Omega

  2. 容性电抗 X_C：

    X_C = \frac{1}{2\pi fC} = \frac{1}{2\pi \times 50\,\text{Hz} \times 100\times10^{-6}\,\text{F}} = 31.8\,\Omega

  3. 复阻抗 Z：

Z = R + j\bigl(X_L - X_C\bigr) = 10 + j\,(47.1 - 31.8) = 10 + j\,15.3\;\Omega \\ \lvert Z\rvert = \sqrt{10^2 + 15.3^2} \approx 18.3\,\Omega

  1. 功率因数 \cos\phi：

\begin{align} {相角\ } \phi &= \arctan\!\biggl(\frac{X_L - X_C}{R}\biggr) = \arctan\!\biggl(\frac{15.3}{10}\biggr) \approx 56.5^\circ \\ {功率因数\ } \cos\phi &= \frac{R}{\lvert Z\rvert} = \frac{10}{18.3} \approx 0.547 \end{align}


我们已经在本教程中看到，阻抗（符号 Z）是对交流电路中电流流动的阻碍，是电阻和电抗的综合效应。我们也已经看到，复阻抗并不等于电路中电阻分量和电抗分量的数学和，而是它们的向量和，因为电抗分量与电阻分量相位相差 90°。

串联电路中的复阻抗遵循与纯电阻电路相同的欧姆定律规则。

即：

Z_T = Z_1 + Z_2 + Z_3 + Z_4 + \dots


那么并联连接的电路又如何计算呢？

并联阻抗

Parallel Impedances

如果一个单个电阻和一个单个电抗并联连接，就必须先求出每个并联支路的阻抗。但由于并联中只有两个元件 R 和 X，我们可以使用两个电阻并联的标准公式。它表示为：

Z_T = \frac{Z_1 Z_2}{Z_1 + Z_2} = \frac{R\,X}{\sqrt{R^2 + X^2}}


其中： Z、 R 和 X 均以欧姆（Ω）为单位。

请注意，由于我们处理的是交流电源和频率，因此电阻分量与电抗分量相位相差 90°，因而在计算它们的乘积时要除以R 和 X 的向量和。

因此，如果 n 条包含复阻抗的支路并联，则电路的总阻抗相当于所有并联支路阻抗的向量和。因此，电路总阻抗的倒数表示为：

\frac{1}{Z_T} = \frac{1}{Z_1} + \frac{1}{Z_2} + \frac{1}{Z_3} + \frac{1}{Z_4} + \dots \\ \therefore Z_T = \frac{1}{\displaystyle \frac{1}{Z_1} + \frac{1}{Z_2} + \frac{1}{Z_3} + \frac{1}{Z_4} + \dots}

并联电路中的电阻和感抗

Resistance and Inductance in Parallel

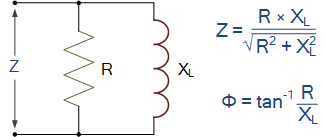
并联电路中的电阻和容抗

Resistance and Capacitance in Parallel

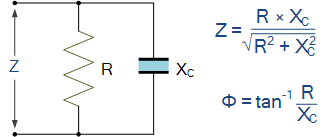
并联电阻中的电阻，容抗及感抗

Resistance, Inductance and Capacitance in Parallel

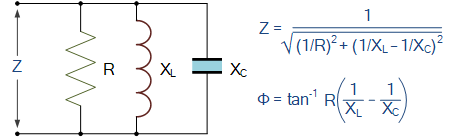
请注意，对于此 RLC 并联电路，在谐振频率处， X_L = X_C，使得净电抗为零，电路中仅存在电阻 R。因此仅在谐振时，动态阻抗定义为：

Z = R

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途

20.功率因数校正
22.波形的形状因数

Comment