Logo

Menu

张彤
张彤
Published on 2025-07-14 / 5 Visits
0
0

20.功率因数校正

功率因数校正

Power Factor Correction

功率因数校正通过并联电容器来抵消感性元件的影响，并减小电压与电流之间的相位差。

功率因数校正是一种利用电容器减少交流电路无功功率分量，以提高电路效率并减小电流的技术。

在直流（DC）电路中，连接负载所耗散的功率可简单地计算为直流电压与直流电流的乘积，即 V \times I，单位为瓦特（W）。

对于固定电阻负载，电流与施加电压成正比，因此电阻负载所耗散的电功率呈线性关系。 然而，在交流（AC）电路中，情况略有不同，因为电抗会影响电路的行为。

对于交流电路，任意时刻的瞬时功率（瓦特）等于该时刻电压与电流的乘积。这是因为交流电压（及电流）为正弦波形，其幅值和方向随时间连续变化，变化速率由电源频率决定。

在直流电路中，平均功率就是 V \times I，但在交流电路中，平均功率并不相同，因为许多交流负载包含感性元件（如线圈、绕组、变压器等），电流与电压之间存在一定的相位差，导致实际耗散功率（瓦特）小于电压与电流乘积。

这是因为在同时含有电阻和电抗的电路中，还必须考虑它们之间的相位角 \theta。

在关于正弦波形的教程中我们了解到，相位角 (\angle \theta) 表示电流相对于电压滞后的电角度。 对于纯电阻负载，电压与电流“同相”，因为不存在电抗。

然而，在含有电感器、线圈或其他感性负载的交流电路中，其感抗 X_L 会产生相位角，使电流相对于电压滞后 90^{\circ}。

因此，电路同时具有电阻 R 和感抗 X_L（单位均为欧姆），它们的综合效应称为阻抗。 于是，阻抗用大写字母 Z 表示，是电路电阻与电抗综合作用后得到的等效欧姆值。

RL 串联电路

RL Series Circuit

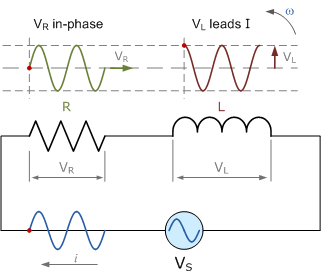
由于这是串联电路，电流在电阻和电感中相同，因此加在电阻上的电压 V_R 与串联电流同相，而加在电感上的电压 V_L 超前电流 90^{\circ}（ELI）。

因此，电阻上的电压向量与电流向量重合（两者同相），而电感线圈上的电压向量则因为电压超前电流 90^{\circ} 而沿垂直方向绘制。

于是，每个元件的向量图都以电流向量为参考，根据其相对位置绘制两条电压向量。

RL向量图

R and L Vector Diagrams

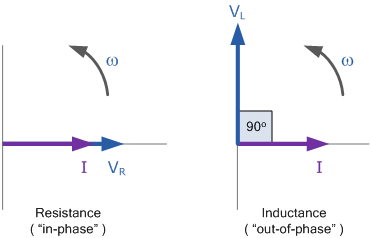
电阻上的电压 V_R 绘制在水平的 实轴 上，而电感上的电压 V_L 绘制在垂直的 虚轴 上。 因此，要获得串联电路两端的合成电压 V_S，必须以电流为参考，将这两个电压向量相加。由于 V_R 与 V_L 构成一 直角三角形，可利用 毕达哥拉斯定理 直接求得合成向量电压：

V_S=\sqrt{\,V_R^{2}+V_L^{2}\,}.

串联RL电路的相量图

Phasor Diagram for the Series RL Circuit

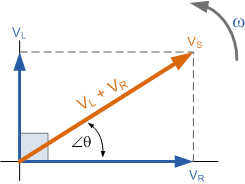
V_R 与 V_L 的相量和不仅通过毕达哥拉斯公式

V_S^{2}=V_R^{2}+V_L^{2}


给出了 V_S 的幅值，还确定了 V_S 与电流 i 之间的 相位角 \angle\theta。因此，可利用 正弦、余弦 或 正切 任意一种三角函数来求得该相位角。

功率因数校正例 1

一个 RL 串联电路由电阻 R=15, \Omega 和感抗 X_L=26, \Omega 的电感组成。如果电流 I=5\,\mathrm{A} 流过电路，计算：

  1. 电源电压 V_S。

  2. 电源电压与电路电流之间的相位角 \theta。

  3. 绘制相应的相量图。

  1. 电源电压 V_s

    V_R = I \times R = 5 \times 15 = 75\;\mathrm{V} \\ V_L = I \times X_L = 5 \times 26 = 130\;\mathrm{V} \\ V_S = \sqrt{V_R^2 + V_L^2} = \sqrt{75^2 + 130^2} = 150\;\mathrm{V_{RMS}}

    检查结果，使用电抗检查:

    Z = \sqrt{R^2 + X_L^2} = \sqrt{15^2 + 26^2} = 30\;\Omega \\ V_S = I_S \times Z = 5 \times 30 = 150\;\mathrm{V_{RMS}}

  2. 相位角 \theta，使用三角函数求解：

    \cos\phi = \frac{V_R}{V_S},\quad \sin\phi = \frac{V_L}{V_S},\quad \tan\phi = \frac{V_L}{V_R} \\ \therefore \cos\phi = \frac{75}{150} = 0.5,\quad \text{因此}\;\phi = 60^\circ

  3. V_s的相量图:

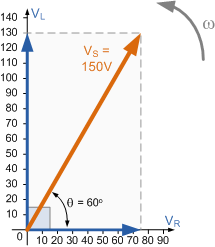
计算得出电阻两端的电压降（实部）为

V_R = 75\;\mathrm{V}

而电感两端的电压（虚部）为

V_L = 130\;\mathrm{V}

显然，75 + 130 = 205 远大于计算得到的 150\;\mathrm{V}。这是因为 150\;\mathrm{V} 代表的是 相量和。已知各电压降和阻抗后，可以将这些值转换为表示电路中消耗功率（有功或无功）的量。

RL 串联电路中的功率

Power in a RL Series Circuit

在含电抗的电路中，电流 i 会根据电抗的性质（容性或感性）超前或滞后电压。电阻所消耗的功率称为 有功功率，符号 P（或 W）。

  • 有功功率也可表示为

    P = I^2 R

    其中 R 是电路的总电阻。

  • 为了用有效值电压和电流表示有功功率，需要乘以相位角的余弦：

    P = V_{\text{rms}}\,I_{\text{rms}}\cos\theta

    对于纯电阻负载，相位角 \theta=0，因此 \cos\theta=1，此时

    P = V_{\text{rms}}\,I_{\text{rms}}


    与 I^2R 结果相同。以本例为例，15 Ω 电阻消耗的有功功率为：

    P_R = I^2 R = 5^2 \times 15 = 375\;\mathrm{W}

    或

    P_R = V_R\,I\cos\theta = 75 \times 5 \times 1 = 375\;\mathrm{W}

当电压与电流不同相（因含电抗）时，电压与电流之积 V\times I 称为 视在功率，单位为伏安（VA），符号为 S。

  • 对于纯感性电路，电流滞后电压 90^\circ，感性无功功率为

    V\,I\cos(90^\circ)=V\,I\times 0=0


    因此感抗不消耗有功功率，但交流电路中仍存在这种“无功”能量交换，称为 无功功率，单位为伏安无功（VAR），符号 Q，对感性负载记作 Q_L。

  • 同理，对于纯容性电路，电流超前电压 90^\circ，容性无功功率

    V\,I\cos(-90^\circ)=0


    称为容性 无功功率，记作 Q_C，通常取负值（-Q_C）。

在本例中，电感无功功率为：

Q_L = I^2 X_L = 5^2 \times 26 = 650\;\mathrm{VAR}


也可按

Q_L = V_{\!L}\,I\,\sin\Theta = 130 \times 5 \times \sin(90^\circ) = 650\;\mathrm{VAR}


然后我们可以看到，无功功率（VAR 部分）的幅值与有功功率相同，但不具有相位角。也就是说，无功功率始终位于 90^\circ 垂直轴上。因此，如果我们知道：

P_R = I^2R = 5^2 \times 15 = 375\;\mathrm{W}

和

Q_L = I^2X_L = 5^2 \times 26 = 650\;\mathrm{VAR}

就可以构建一个功率三角形来展示 P、Q 与 S 之间的关系。

感性功率三角形

Inductive Power Triangle

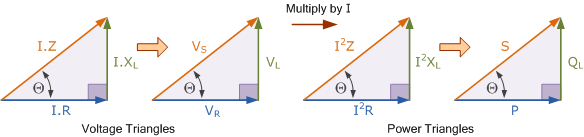
容性功率三角形

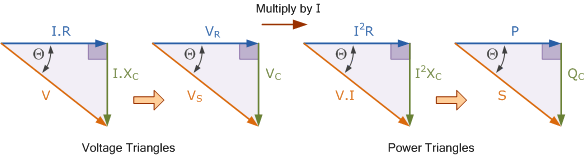
我们可以再次使用前述的毕达哥拉斯定理以及三角函数：正弦（\sin）、余弦（\cos）和正切（\tan）来定义功率三角形。

功率三角形等式

Power Triangle Equations

我们可以再次使用前述的毕达哥拉斯定理以及正弦、余弦和正切三角函数来定义功率三角形。

\mathrm{VA}^2 = W^2 + \mathrm{VAR}^2 \quad\Longrightarrow\quad S^2 = P^2 + Q^2


\mathrm{VA} = \sqrt{W^2 + \mathrm{VAR}^2} \quad\Longrightarrow\quad S = \sqrt{P^2 + Q^2}


功率因数 \mathrm{pf} 定义为：

\mathrm{pf} = \cos\phi = \frac{\text{有功功率}}{\text{视在功率}}


\mathrm{pf} = \cos\phi = \frac{W}{\mathrm{VA}} = \frac{P}{S}


\mathrm{pf} = \sin\phi = \frac{\mathrm{VAR}}{\mathrm{VA}} = \frac{Q}{S}


\mathrm{pf} = \tan\phi = \frac{\mathrm{VAR}}{W} = \frac{Q}{P}


有功功率 P 与无功功率 Q 由下式给出：

P = \mathrm{VA}\,\cos\phi, \quad Q = \mathrm{VA}\,\sin\phi


功率因数校正例2

一个线圈具有电阻 10\,\Omega 和电感 46\,\mathrm{mH}。当它接入 100\,\mathrm{V_{rms}},\;60\,\mathrm{Hz} 的电源时，若电流为 5\,\mathrm{A}，计算：

  1. 各元件两端的电压。

  2. 电路的相位角。

  3. 串联 RL 电路消耗的各种功率。

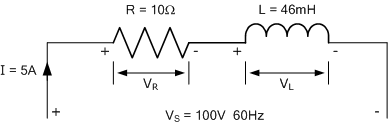
首先得到电抗:

X_L = 2\pi f L = 2\pi \times 60 \times 46\times10^{-3} = 17.34\;\Omega


R = 10\;\Omega


Z = \sqrt{R^2 + X_L^2} = \sqrt{10^2 + 17.34^2} = 20\;\Omega


其中， X_L 为感抗， R 为电阻， Z 为阻抗。

1）电阻两端的电压 V_R 与电感两端的电压 V_L

V_R = I \times R = 5 \times 10 = 50\;\mathrm{V}\\ V_L = I \times X_L = 5 \times 17.34 = 86.7\;\mathrm{V}\\ V_S = \sqrt{V_R^2 + V_L^2} = \sqrt{50^2 + (86.7)^2} = 100\;\mathrm{V}

2）电路的相位角 \theta

\cos\phi = \frac{V_R}{V_S},\quad \sin\phi = \frac{V_L}{V_S},\quad \tan\phi = \frac{V_L}{V_R}\\ \therefore \cos\phi = \frac{50}{100} = 0.5 \quad\Longrightarrow\quad \phi = 60^\circ


3）电路的功率（有功功率 P、无功功率 Q 及视在功率 S）

P = V\,I\cos\phi = 100 \times 5 \times \cos(60^\circ) = 250\;\mathrm{W}\\ Q = V\,I\sin\phi = 100 \times 5 \times \sin(60^\circ) = 433\;\mathrm{VAR}\\ S = V\,I = 100 \times 5 = 500\;\mathrm{VA}


我们可以确认，电路从电源吸取了 500\,\mathrm{VA} 的复功率，因为

S = I^2 Z = 5^2 \times 20 = 500\;\mathrm{VA}


构建功率三角形也能验证这一点。

然而，串联 RL 电路所消耗的这一视在功率很大，是因为电压相对于电流（ELI）的相位角 \theta 也很大，导致功率因数仅为 \cos(60^\circ)=0.5，且呈滞后。因此，需要通过添加与电路感性无功功率（433 VAR）相反类型的电抗来抵消线圈为维持磁场而消耗的部分无功功率。

我们是否应该关注线圈的低功率因数？答案是肯定的。因为功率因数是线圈的有功功率与其视在功率之比（W/VA），它表明所供电能的利用效率。功率因数低意味着所供电能未被充分利用——在本例中，50% 的功率因数（250/500）仅用 500 VA 电能输出 250 W 有功功率。

既然线圈的感抗为正，就必须加入为负的容抗来抵消，以改善线圈的总功率因数。向电路中添加电容以减小相位角和无功功率的做法称为功率因数校正，可以使电路功率因数趋近于 1（单位功率因数）。

功率因数校正

功率因数校正可以改善电源电压与电流之间的相位角，而有功功率（瓦特）保持不变，因为正如我们所见，纯电抗不消耗任何有功功率。在上述线圈并联加入容性电抗形式的阻抗，将减小 \theta，从而提高功率因数，进而减少电路从电源汲取的有效值电流。

交流电路的功率因数可在 0 到 1 之间变化，取决于感性负载的强度，但实际上即使是最强的感性负载，其功率因数也不会低于约 0.2。

如上所述，功率因数小于 1 意味着存在无功功率消耗，且随着功率因数趋近于 0（完全感性）而增加。显然，功率因数恰好为 “1” 意味着电路不消耗任何无功功率（完全电阻性），其功率因数角为 0^\circ，这称为“单位功率因数”。

在上述线圈并联电容不仅可减少不需要的无功功率，还可减小电源端的总电流。理论上，电容器可提供电路所需的 100% 补偿无功功率，但在实践中，95% 至 98%（0.95 至 0.98）的功率因数校正通常已足够。

因此，针对上例 No.2 中的线圈，需要多大电容量的电容器才能将功率因数从 0.5 提高到 0.95？

功率因数 0.95 对应的相位角为：

\cos\Phi = 0.95 \quad\Longrightarrow\quad \Phi = 18.2^\circ


因此，需要的无功功率为：

\tan\bigl(18.2^\circ\bigr) = \frac{Q}{P} = \frac{\mathrm{VAR}}{\mathrm{W}} = 0.329 0 = \frac{\mathrm{VAR}}{250} \\\quad\therefore\quad \mathrm{VAR} = 250 \times 0.329 = 82.2\;\mathrm{VAR}


因此，对于相位角 18.2^\circ，所需的无功功率为 82.2\;\mathrm{VAR}，若原始未校正的无功功率为 433\;\mathrm{VAR}，而新计算值为 82.2\;\mathrm{VAR}，则需减少 433 - 82.2 = 350.8\;\mathrm{VAR}（容性）。因此：

\mathrm{VAR}_{(\text{容性})} = Q_C = 350.8 \\ Q_C = 350.8 = \frac{V_S^2}{X_L} = \frac{100^2}{X_L} \\ \therefore X_L = \frac{100^2}{350.8} = 28.5\;\Omega


要使无功功率降至 82.2 VAR，所需电容器在额定频率下的容抗为 28.5 Ω。因此，该电容器的电容量按下式计算：

X_C = 28.5\,\Omega = \frac{1}{2\pi f C} \\ \therefore C = \frac{1}{2\pi \times 60 \times 28.5} = 93\,\mu\mathrm{F}


因此，要将例 2 中线圈的功率因数从 0.5 提高到 0.95，需要并联一个 93 μF 的电容器。 利用上述数值，我们现在可以计算功率因数校正后，电源所提供的视在功率。

新的视在功率值

\mathrm{VA} = \sqrt{W^2 + \mathrm{VAR}^2} \quad\Longrightarrow\quad S = \sqrt{P^2 + Q^2} \\ S = \sqrt{250^2 + 82.2^2} = 263\;\mathrm{VA}


我们还可以构建功率三角形，如图所示展示校正前后视在功率 S（VA）和无功功率 Q（VAR）的数值。

功率三角形

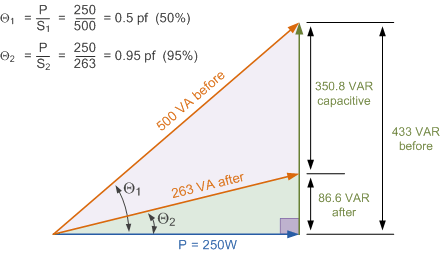
如果电路的视在功率已从 500\;\mathrm{VA} 降低到仅 263\;\mathrm{VA}，那么可计算所提供的有效值电流为：

S = V \times I

因此：

I = \frac{S}{V} = \frac{263}{100} = 2.63\;\mathrm{A}

仅通过在线圈两端并联一个电容器，不仅将其整体功率因数从 0.5 提高到 0.95，还将供电电流从 5 A 降低到 2.63 A，减少约 47%。最终电路示意图如下：

最终功率因数校正电路

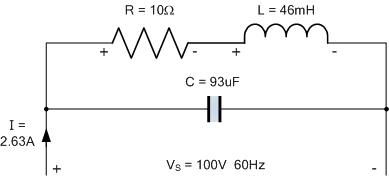
如果需要，您也可以将本例中计算得出的 93 μF 电容增加到最大 114.8 μF，从而将功率因数从所需的 0.95 进一步提高到 1.0（单位功率因数）。实际上，对于本例，使用一个标准的 100 μF 无极性电容就足够了。

在本教程中，我们已经看到，由于感性负载导致的滞后功率因数会增加交流电路中的功率损耗。通过在感性负载两端并联一个合适的容性电抗元件（即电容器），可以减小电压与电流之间的相位差。

这能够降低电路的视在功率（即有功功率与视在功率之比——功率因数），同时改善电路的电能质量并减少所需的电源电流。该技术称为“功率因数校正”。

附录

110 kV 变电站无功功率补偿

某地区一 110 kV 送电母线，向下游工业园区供电。该园区有功功率为

P = 100\;\mathrm{MW}

但因大批电动机等感性负载，母线功率因数仅为

\mathrm{pf}_1 = 0.80

需要将功率因数提高到

\mathrm{pf}_2 = 0.95

以减少线路损耗、提高电能质量。

  1. 计算补偿前的视在功率与无功功率

    S_1 = \frac{P}{\mathrm{pf}_1} = \frac{100}{0.80} = 125\;\mathrm{MVA} \\ Q_1 = \sqrt{\,S_1^2 - P^2\,} = \sqrt{125^2 - 100^2} = 75\;\mathrm{MVar}

  2. 计算补偿后所需的无功功率

    S_2 = \frac{P}{\mathrm{pf}_2} = \frac{100}{0.95} \approx 105.26\;\mathrm{MVA} \\ Q_2 = \sqrt{\,S_2^2 - P^2\,} = \sqrt{105.26^2 - 100^2} \approx 32.30\;\mathrm{MVar}

  3. 确定并联电容器需补偿的无功功率

    Q_C = Q_1 - Q_2 = 75 - 32.30 = 42.70\;\mathrm{MVar}

  4. 计算电容器总电容量 对三相系统，电压线–线有效值为

    U = 110\;\mathrm{kV},\quad f = 50\;\mathrm{Hz}


    则三相总容抗满足

    Q_C = \frac{3\,U^2}{X_C} \quad\Longrightarrow\quad X_C = \frac{3\,U^2}{Q_C}

    容量

    C = \frac{1}{2\pi f\,X_C} = \frac{1}{2\pi \times 50 \times \bigl(\tfrac{3U^2}{Q_C}\bigr)} \approx \frac{Q_C}{2\pi f\,3 U^2} \approx 11.2\;\mu\mathrm{F}

结果：

  • 并联约 42.7 MVar 的电容器组

  • 每相约 11.2 μF 的电容量

效果：功率因数从 0.80 提高到 0.95，减少无功功率交换，降低线路电流与损耗，提升电网运行效率和电能质量。

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途

19.功率三角形与功率因数
21.阻抗与复阻抗

Comment