正弦波

Sine Wave

正弦波是一种周期性波形，可通过在单位圆上绘制三角函数的正弦曲线来最佳描述。

什么是正弦波？

正弦波，也称为正弦波形或正弦波，是一种光滑的、周期性的振荡，描述了空间或时间中的重复模式。它是电气工程中最简单、也最广泛使用的波形类型之一。正弦波是在“时域”中存在的周期信号。因此，它们可用于分析线性电气系统在特定频率范围内的频率和/或相位响应。

正弦波形通常通过旋转交流发电机或交流发电机（alternator）利用电磁感应产生。如果我们以恒定速度在均匀磁场中旋转单根线圈，所产生的电压将呈现出典型的正弦波形。因此，在任何瞬时，所产生的电压取决于线圈导体与磁力线之间的相对位置。

例如，如果线圈导线的运动方向与磁力线平行，则几乎没有磁力线被切割，产生的电压为零。同样，如果线圈导线的运动方向与磁力线垂直，则在该瞬时切割的磁通量最多，从而产生最大电压。

磁场正弦波产生

Magnetic Field Sine Wave Generation

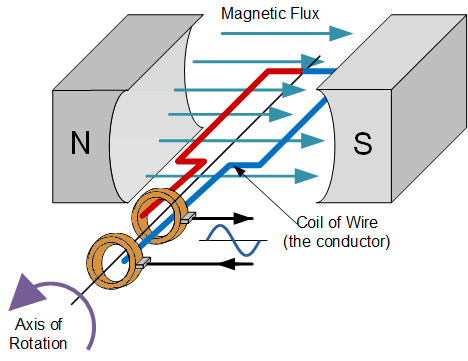
因此，在均匀磁场中线圈的持续旋转会导致与线圈相连的磁通量不断变化。随着线圈的旋转，这一过程在线圈中产生了一个正弦波电压。

不仅如此，正弦电压（或电流）不仅以规则的间隔改变方向，其幅值也随着线圈的旋转而连续变化。然而，这种周期性波形仅在旋转持续时才会存在。

由于所产生的电压波形随时间呈正弦变化，它具有若干可用于描述的参数，例如：

正弦波的特性：

✓ 幅值 (A)： 相对于原点的最大位移（正或负），即正弦波的峰高。

✓ 周期 ( T)： 波形完成一个完整循环所需的时间。

✓ 频率 ( f)： 每秒重复的次数。频率是周期的倒数， \displaystyle f = \tfrac{1}{T}。

✓ 相位 ( \theta)： 沿水平轴的偏移量，决定正弦波的起始位置。

由此可见，正弦波是一种随时间变化的信号，其“正弦波形”定义了所产生信号的形状。正弦波瞬时值作为时间的函数可用下面的正弦波方程来表示：

即瞬时值a(t) 等于最大值乘以该时刻的角度正弦。

这一通用数学表达描述了正弦波随时间的产生。那么，它究竟意味着什么？作为周期性波形，正弦波也可以通过数学三角函数来生成，这些函数用角度的正弦函数或余弦函数来表达。

正弦波的数学表示

Mathematical Representation of a Sine Wave

三角函数——正弦和余弦——都是周期函数，因此我们可以用它们来定义单位圆上某点的坐标。

基本上，单位圆定义为半径为 1 的圆（ r = 1），其圆心位于横轴（实轴）和纵轴（虚轴）的交点处。单位半径对应一个可变角度 \theta，该角度可绕完整的 360° 周长旋转。通常， \theta 从正实轴沿逆时针方向测量，如下所示。

正弦波单位圆

Sine Wave Unit Circle

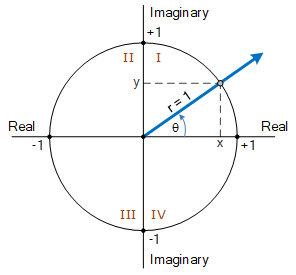
由于圆的周长 C 等于圆的直径 D 与 \pi 的乘积，确定圆的周长的标准数学公式为：

然而，圆的直径 D 也是其半径 r 的两倍，因为半径的长度是直径长度的一半。因此 D = 2r。于是我们可以正确地写出：

因此，如果单位圆的半径等于 1（r = 1），其周长将为 2\pi。换句话说，沿单位圆周长进行一次完整旋转，其长度等于 2\pi 个单位。

我们从学校时代也知道，圆周上一圈的度量是 360°。那么单位圆周长可被分为 360 等分的度数时，圆周长度 2\pi 对应的单位是什么呢？

正弦波的弧度测量

Radian Measurement of a Sine Wave

还有另一种角度测量单位，称为 弧度。弧度（rad）是圆心所对的两条半径之间的角度，这两条半径在圆周上截取的弧长等于半径的长度。如下图所示，对应一个弧长等于半径的圆弧，其中心角即为 1 弧度。

正弦波的弧度示意

The Radian of a Sine Wave

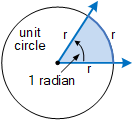
显然，当考虑单位圆时，度与弧度之间必然存在对应关系。若半径为 r 的圆的周长为 2\pi r，则单位圆中共有

弧度。同时，圆周上也有 360 度，这就给出了弧度与度的比值：完整一圈为 2\pi 弧度对应 360°，半圈为 \pi 弧度对应 180°。由此得出：

我们可以建立一个角度值表，将 \theta 从 0^\circ 到 360^\circ（一整圈），以 15^\circ 为步长（或任意所需步长）进行度数到弧度的转换，如下所示。

角度-弧度对应表

以下为与图中对应的 Markdown 表格：

既然已经确定了圆的周长 C 可以分为度数或弧度两种角度度量，如果将单位圆的周长展开成一条等长的直线，就为正弦波波形的构建提供了水平 x 轴的基础，如下所示。

正弦波波形的水平轴

Horizontal-axis for a Sine Wave Waveform

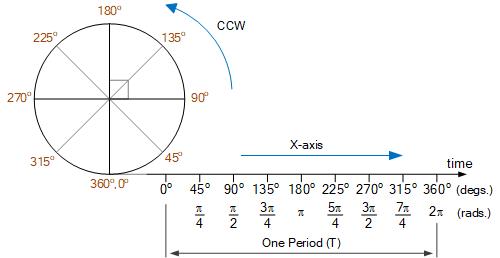
然后我们可以看到，将圆沿逆时针方向恰好旋转一整圈直到与自身重合所形成的角度为 360 度。因此，一个角度 1° 等于一次旋转的 1/360。由此可知，一个直角 90° 代表旋转的 1/4，而 180° 则代表旋转的 1/2。

显然，如果我们继续旋转圆圈第二次或第三次，水平 x 轴上将重复相同的角度序列。因此，该函数具有周期性，周期 T 为 2\pi。一旦我们知道了长度为一个周期的区间内的轴值，就可以得知所有角度对应的正弦值，无论是以度数还是弧度为单位。

正弦波的三角学

Trigonometry of a Sine wave

好的，现在我们已经理解了为什么正弦波的水平 x 轴可以使用度数或弧度。在此基础上，我们可以利用三角学来构建垂直 y 轴，用以表示波形的振幅。

三角学研究三角形的边与角之间的关系。因此，我们可以使用直角三角形来图形化地创建正弦波的波形，其中一种直观的方式是借助向量。

向量vector是一条既指示空间中某一点位置的方向，又指示其大小的线段。向量的长度表示其大小，方向则由其旋转角度表示。为了代数化地表示向量，我们需要借助毕达哥拉斯定理——它正是用于求解直角三角形的边长和角度的基本定理。

毕达哥拉斯定理Pythagoras’ theorem在正弦波的定义和理解中起到关键作用，尤其是在三角学中的单位圆上下文中。正弦函数与直角三角形之间的关系，可用于在水平轴上可视化并定义正弦波。

毕达哥拉斯与单位圆

Pythagoras and the Unit Circle

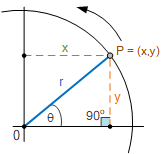
取前面半径为 1 的单位圆，其圆心位于坐标平面的原点。如果我们取圆周上任意一点，并从该点向水平轴（ x 轴）做一条垂线（ y），就可以构造一个直角三角形。然后，我们可以利用毕达哥拉斯定理来描述该直角三角形的任意边与所形成角度之间的关系。

如其名称所示，直角三角形是指其三个内角中有一个是直角（90°）的三边形。与直角相对的最长边称为斜边（Hypotenuse，记作 H）。

与角 \theta 邻接的那一条直角边称为邻边（Adjacent，记作 A），而与角 \theta 对应的那一条直角边称为对边（Opposite，记作 O）。

因此，对于单位圆上任意一点，斜边就是圆的半径 r，对于单位圆有 r=1。水平距离（邻边）就是该点的 x 坐标，垂直距离（对边）就是该点的 y 坐标。半径与 x 轴所夹的角度就是正弦和余弦函数所涉及的 \theta。

用毕达哥拉斯定理定义正弦和余弦

角 \theta 的正弦 \sin(\theta) 定义为对边（垂直方向的 y 值）与斜边（半径）的比值：

角 \theta 的余弦 \cos(\theta) 定义为邻边（水平 x 轴方向的长度）与斜边的比值：

因此，对于任意角度 \theta，将旋转向量投影到水平轴上时，其对应的正弦函数值即给出了单位圆上表示瞬时值的点在垂直方向（高度）上的大小。随着角度 \theta 从 0^\circ 增加到 360^\circ，正弦函数描绘出平滑的、周期性的波形。这条正弦曲线即代表了一个正弦波。

从单位圆可视化正弦波

Visualization of a Sine Wave from the Unit Circle

一旦确定了某角度的正弦值，就可以利用毕达哥拉斯定理求得该点相对于水平 x 轴的垂直高度。由于单位圆的斜边长度为 1，给定单位圆上任意点 P 对应的角度 \theta，我们可以将之前的正弦方程重新排列，从而在 0^\circ 到 360^\circ 的区间内，以表格形式求出各角度对应的 y 值。

正弦波表

然后我们可以看到，随着点 P(x,y) 在单位圆的圆周上移动，其纵坐标 y=\sin(\theta) 以周期性的方式变化。如果我们将 \sin(\theta) 的取值相对于旋转角度（或时间 t）在之前的水平轴上作图，得到的图形就是一个平滑的、重复的正弦波，其周期或循环如图所示。

正弦波函数图

Graph of the Sine Wave Function

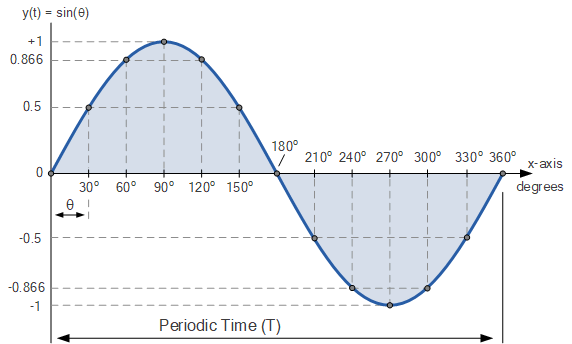
正弦曲线 y = \sin\theta 表明，

当我们在 0^\circ 到 360^\circ（2\pi）范围内绘制各点时，随着 \theta 从 0^\circ 增加到 90^\circ（\pi/2）， y 的值从 0 增加到 1；

当 \theta 从 90^\circ（\pi/2）增加到 180^\circ（\pi）时，y 的值又从 1 减小到 0，再继续减小到 –1；

最后，当 \theta 从 270^\circ（3\pi/2）增加到 360^\circ（2\pi）时， y 的值则从 –1 增加回 0。

如果以更短的间隔绘制y的值，例如每 10^\circ（共 36 个点）或每 5^\circ（共 72 个点），则会得到更精确的结果，从而构造出更准确的正弦波形。

注意，对于大于360^\circ（2\pi）的偏移角度，三角函数的值只是重复出现。例如， 390^\circ（360+30）或 750^\circ（2\times360+30）的正弦（或余弦）值，与原始 30^\circ 的值完全相同。

由此可见，数学上的正弦函数与直角三角形的几何紧密相连，并且由于毕达哥拉斯定理的作用，只要我们改变角度 \theta，就能根据单位圆中所构成三角形边的比值描绘出正弦波。

因此，毕达哥拉斯定理帮助我们理解正弦函数的几何基础，这对于定义正弦波至关重要。

正弦波示例 1

假设某正弦波的最大电压 V_{\max}=100 伏特，求其在旋转角度 45^\circ 时的瞬时电压。

因此，当向量旋转到第一象限的 45^\circ 位置时，其幅值为 70.7 伏特。同样地，当旋转 90^\circ（达到第二象限的 135^\circ）时，向量的幅值也同样为 70.7 伏特。

正弦波的角速度

我们已经看到，正弦波可视为以恒定速度做圆周运动的单个向量的周期性运动。所绘制波形的水平 x 轴以时间为单位，垂直 y 轴则表示波形的幅值（电压或电流）。

向量完成一次完整旋转所用的时间称为周期，用符号 T 表示。因此，一次完整旋转即一个周期。周期的倒数即为频率 f，即 f = \frac{1}{T}.

电气频率 f 表示每秒钟的循环次数，以赫兹（Hz）为单位。例如，如果正弦波每秒重复一次，则其频率为 1 Hz；若每秒重复 50 次，则频率为 50 Hz；每秒重复 60 次则为 60 Hz，依此类推。

由于向量一次完整旋转（一个周期）对应 360^\circ，因此在 t 秒内总共旋转的角度可表示为 360\,f\,t.而我们亦知，一个周期 360^\circ 等于 2\pi 弧度，于是可将 360\,f\,t 替换为 2\pi f t。这便称为正弦波的角速度。对应的余弦函数也具有相同的周期 2\pi。

因此，我们可将正弦波的表达式改写为以弧度为角度单位的更通用形式：

由于正弦波的角速度定义为 2\pi f 弧度每秒，我们通常用希腊字母 \omega（omega）表示该量，即 \omega = 2\pi f,从而 2\pi f t = \omega t。这就是向量在 0 \le \omega t \le 2\pi 之间以弧度每秒为单位的角速度。实际上，频率越高，角速度也越大。

正弦波示例 2

周期为 16.67 毫秒的正弦波，其角速度是多少？

到目前为止，我们是假设正弦波图 y(t) = A_{\max}\sin(2\pi f t)（以度数为单位）或 y(t) = A_{\max}\sin(\omega t)（以弧度为单位）都在水平 x 轴的零点通过。但如果波形不经过零点，或者我们想表示两个相同频率波形之间的角位移（例如电压与电流波形），会怎样呢？

电压波形可能在零点通过时，而电流波形可能已经通过或尚未通过同一旋转方向的零交叉点。换言之，这两个相同频率的正弦波在 x 轴上有两个不同的零交叉点。

此时，我们就说这两个波形之间发生了相位角的偏移。也就是说，相对于电压正弦波，电流波形有一定量的相移，用度或弧度表示。例如，相移为 30^\circ 或 \pi/6。

那么，如何在基本正弦波方程中表示这种相位差呢？只需在方程中加入 \Phi（希腊字母 Phi），得到更通用的正弦波表达式：

注意，当波形在水平轴零点通过时， \Phi = 0。此时 A_{\max}\sin(\omega t \pm 0) = A_{\max}\sin(\omega t)。此外，正弦波可以相对于参考波形向左或向右平移。

通常，先通过零点的波形称为“超前”，而后通过的则称为“滞后”。具体取决于哪一个波形作为参考。下面给出一个示例。

两个正弦波形之间的相位差示意图

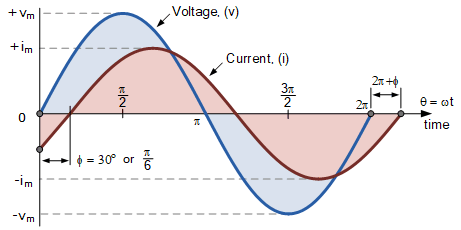
电压波形（蓝色）如上所示，在水平 x 轴的零点处开始，而在同一时刻，电流波形（红色）仍为负值，直到 30° 之后才通过该参考轴。

此时，由于电流在电压波形之后 30° 才经历零交叉并达到其最大峰值和零值，两者之间存在相位差。

由于两条波形不再“同相”，它们因此以由 Φ 决定的量“错相”，在本例中为 30°。也就是说，电流波形相对于电压波形滞后相位角 Φ = 30°。

正弦波示例 3

以下电压和电流波形之间的相位差是多少？

已知：

则电流 i 相对于电压 v 超前：

已知：

则电流 i 相对于电压 v 滞后：

教程小结

我们已经看到，正弦波可以定义为一种连续的、随时间变化的周期性波形，其波形可最佳地用简单的数学表达式 y = \sin(\theta) 来描述，其中 \theta（theta）为角度。

我们还看到，正弦波图形既可以通过在线圈以恒定速度在磁场中旋转来产生，也可以通过在单位圆上利用毕达哥拉斯定理进行数学绘制来生成。注意，正弦波形始终代表交流量，不存在“直流正弦波”。

通过在单位圆上旋转一个或多个向量，我们可以相对于时间绘制正弦波图，其参数包括频率、幅值和相位。波形完成一次 360° 循环所需的时间称为周期 T，可以用度或弧度表示。

单位时间内产生的波形周期数称为频率，以赫兹（Hz）为单位，f = 1/T。而正弦波的角频率（\omega）以弧度每秒（rad/s）为单位，通常表示为 \omega = 2\pi f。相位差 \Phi 则是一个正弦波相对于另一个正弦波超前或滞后的角度差。

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途