最大功率传输
Maximum Power Transfer
当负载电阻的数值等于供电网络的等效电阻时,负载所吸收的功率最大。
最大功率传输定理指出,当负载的电阻值与电压源的内阻相等时,能够向负载提供最大的功率。通常,该内阻(或在包含电感、电容时的内阻抗)为固定值,单位为欧姆(\Omega)。
然而,当我们在电源的输出端连接一个负载电阻 R_{L} 时,负载的阻抗会从开路状态(\infty)变化到短路状态(0),导致负载吸收的功率依赖于电源的实际阻抗。为了使负载吸收尽可能多的功率,负载电阻必须与电源阻抗“匹配”,这便是最大功率传输的基本原理。
最大功率传输定理是另一种有用的电路分析方法,它保证当负载电阻 R_{L} 恰好等于电源内阻 R_{S} 时,负载中将消耗最大的功率。负载阻抗与电源内阻之间的关系决定了负载中的功率。请参考下图电路示意:
戴维南等效电路
Thevenins Equivalent Circuit
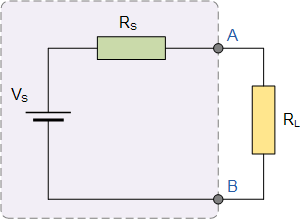
在上述戴维南等效电路中,最大功率传输定理指出:“如果负载电阻的数值等于为其提供功率的网络的戴维南或诺顿等效源电阻,则负载电阻上将消耗最大功率。”
换句话说,要使负载电阻消耗的功率最大,其阻值必须等于等效戴维南源电阻,即
如果负载电阻的数值低于或高于网络的等效源电阻,其消耗的功率将小于最大值。
例如,求在下图电路中能够实现最大功率传输的负载电阻 R_L 的数值。
最大功率传输例题1
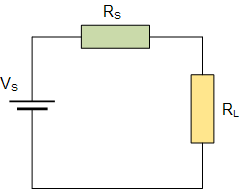
然后,通过使用以下欧姆定律方程:
电路中流过的电流由整个串联电阻决定,所以计算电流时要把电源内阻 R_s 和负载电阻 R_L 相加,
但在最大功率传输定理中,我们重点关注“负载”所能获得的最大功率,所以功率计算里只带入 R_L。
我们现在可以完成以下表格,以确定在不同负载电阻值下电路中的电流和功率。
电流与功率表
利用上表中的数据,我们可以绘制负载电阻 R_{L} 与功率 P 的关系曲线,展示不同负载电阻值下的功率变化。同时注意,当开路(电流为零)或短路(电压为零)时,功率均为零。
功率与负载电阻关系图
Graph of Power against Load Resistance
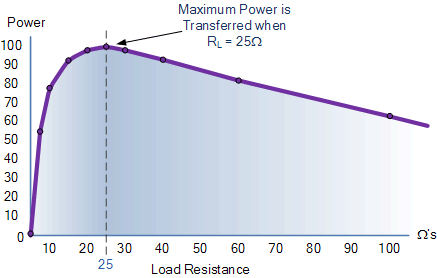
从上表和曲线可以看出,当负载电阻 R_{L} 与源内阻 R_{S} 相等时,即
负载上发生最大功率传输。这称为“匹配条件”,通常情况下,当外部设备的阻抗恰好与源阻抗完全匹配时,主动设备(如电源或电池)向外部设备传送的功率最大。
一个很好的阻抗匹配例子是在音频放大器与扬声器之间。放大器的输出阻抗 Z_{\mathrm{OUT}} 可能标称为 4\Omega 到 8\Omega 之间,而扬声器的额定输入阻抗 Z_{\mathrm{IN}} 标称为 8\Omega。
因此,如果将 8\Omega 扬声器接到放大器的输出端,放大器会将其视为一个 8\Omega 负载。将两只 8\Omega 扬声器并联,相当于放大器驱动一只 4\Omega 扬声器;而这两种配置均在放大器的输出规格范围内。
不当的阻抗匹配会导致过多的功率损耗和热量产生。那么,当放大器和扬声器的阻抗相差很大时,如何实现阻抗匹配呢?市面上有扬声器阻抗匹配变压器,可以将阻抗从 4\Omega 变换到 8\Omega,或到 16\Omega,从而允许多只扬声器按照各种组合(例如公共广播系统)连接时实现阻抗匹配。
阻抗匹配中的最大功率传输
Maximum Power Transfer of Impedance Matching
在放大器电路的输出级中,阻抗匹配用于在源和负载之间提供最大功率传输。信号变压器用于将扬声器的高或低阻抗值匹配到放大器的输出阻抗,以获得最大的声音功率输出。这些音频信号变压器称为“匹配变压器”,如下图所示将负载耦合到放大器输出。
变压器阻抗匹配
Transformer Impedance Matching
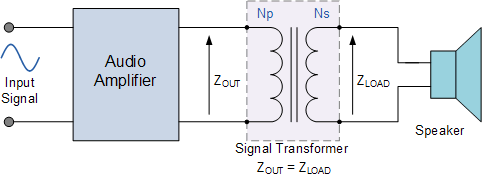
即使输出阻抗与负载阻抗不相同,也可以通过选用合适的“匝比”来实现最大功率传输,使负载阻抗 Z_{\mathrm{LOAD}} 与输出阻抗 Z_{\mathrm{OUT}} 之比与变压器原、副线圈匝数之比相对应,因为变压器一侧的电阻在另一侧会变为不同的数值。
如果负载阻抗 Z_{\mathrm{LOAD}} 和源阻抗 Z_{\mathrm{OUT}} 均为纯电阻,则最大功率传输的匹配条件可表示为:
其中, N_P 为原线圈匝数, N_S 为副线圈匝数。通过改变变压器的匝比,就可以将输出阻抗“匹配”到源阻抗,以实现最大功率传输。例如:
最大功率传输例题2
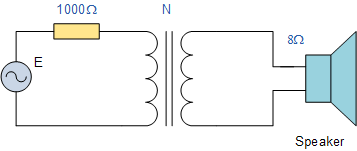
如果要将 8\Omega 的扬声器连接到输出阻抗为 1000\Omega 的放大器,计算为实现音频信号最大功率传输所需的匹配变压器的匝比。假设放大器源阻抗为 Z_{1},负载阻抗为 Z_{2},变压器匝比记为 N。
因此,
通常,在低功率放大电路中使用的小型高频音频变压器几乎总是为了简化而被视为理想变压器,因此可以忽略任何损耗。
在下一个关于直流电路理论的教程中,我们将研究星-三角变换(Star–Delta Transformation),它允许我们将平衡的星形连接电路转换为等效的三角形电路,反之亦然。
附录
最大功率传输的数学推理
要推导最大功率传输定理,我们从等效电路出发,如下图所示:
1. 写出电流与功率表达式
根据欧姆定律,流过负载的电流为
负载上消耗的功率为
2. 对 R_{L} 求极值
为了找到使 P 最大的 R_{L},对 P 关于 R_{L} 求导并令其为零:
化简分子:
令上式为零,且 R_{\mathrm{Th}}+R_{L}\neq0,得
3. 验证是极大值
还可看二阶导数在 R_{L}=R_{\mathrm{Th}} 处为负,即可确认此处为极大值,不赘述。
4. 直观解释
当 R_{L} 很小时,回路电阻小,电流大,但大部分电压降落在内阻上,负载功率小。
当 R_{L} 很大时,电流很小,尽管电压几乎全部加在负载上,但电流微弱,同样功率小。
唯有两者相等时,电压与电流都处于“平衡”,才能使功率 P=I^2R_{L} 达到最大。
最大功率传输的效率问题
在纯电阻匹配( R_L=R_s)时,负载只能得到总功率的 50%,效率看起来很低。但“最大功率传输定理”之所以重要,并不是为了在所有场景下追求 50% 的效率,而有以下几方面的价值:
测量与等效化
通过调节外部可变负载至最大功率点,即可反推出未知网络的等效内阻(或内阻抗)。这在实验室和仪器设计中,是一种快速、可靠的“黑箱”参数测量方法。
信号源受限时的输出优化
在很多小信号/低功率系统(如无线发射机、传感器、音频放大器)中,信号源驱动能力有限,比起效率更关心“能把有限的输出功率都送出去”。
例如:射频功率放大器需要在给定最大输出功率许可范围下,把最大发电功率送到天线;音频功放也要在不超载的情况下输出最大声压级。
阻抗匹配网络带来的效率提升
实际工程中常用无源匹配网络(L 型、Π 型、变压器耦合等)做复阻抗共轭匹配:虽然在等效的纯电阻模型下效率才 50%,但加上变压器和高 Q 值的谐振元件后,这些器件自身的损耗很小,整个系统的真实效率可高达 90% 以上。
换言之,理论上的“50%”仅针对最简模型;实际设计里,匹配网络本身是高效的无源元件,真正废掉的功率远低于 50%。
设计与教学价值
最大功率传输定理是电路理论的重要组成,让我们理解电源、负载和网络之间的功率分配关系,也为后续的共轭匹配、S-参数分析、网络综合等高级概念打下基础。
在教学中,它帮助学生直观地体会“阻抗匹配”“功率分配”与“效率折中”三者之间的内在联系。
场景区分:功率最大 vs. 损耗最小
功率最大:信号质量或输出幅度最关键时(如无线通信、测量、音频推挽),采用最大功率匹配;
损耗最小:大功率输电或配电网中,更看重效率,会让负载阻抗远大于线路阻抗,或通过高电压、低电流方式降低 I^2R 损耗,而不会工作在“内外阻相等”点上。
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

