诺顿定理
Nortons Theorem
诺顿定理将电路简化为一个与恒定电流源并联的单一电阻。
诺顿定理定义
Norton’s Theorem Definition
我们可以将诺顿定理解释为一种分析方法,用于将任意复杂电路转换为由一个与电流源并联的单一电阻组成的简化等效电路。
诺顿定理指出:“任何包含若干能量源和电阻的线性电路,都可以用一个恒定电流源并联一个电阻来替换”。简单来说,诺顿定理允许我们将任何复杂的电路部分替换为更简单的等效电路,从而使电路分析变得更加容易。
对于负载电阻 R_L 而言,这个单一电阻 R_S 是在所有电流源开路后,从网络端口向内看所得到的等效电阻。
电流源(诺顿电流 I_S)等于在所有独立源被关闭时(电压源以短路替代,电流源以开路替代),在负载端短路时流过的短路电流,如下所示。
诺顿等效电路
Nortons equivalent circuit
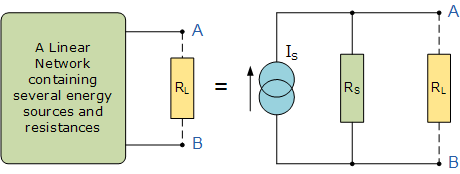
该“恒定电流”的数值,即当将两个输出端短接时所流过的电流;而源电阻则是从端口向内看所测得的阻值(与戴维南等效电路中的测量方法相同)。
诺顿定理示例
考虑我们在上一节中已熟悉的直流电阻电路。
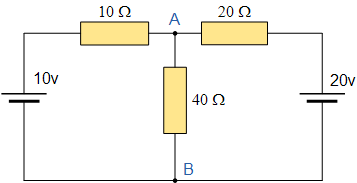
为了求得上述电路的诺顿等效电路,我们首先必须去掉中间的 40\Omega 负载电阻,并将端子 “A” 与 “B” 短接,以得到如下电路。
注意,这里和戴维南定理做法不同,前者是开路处理,这里是短路处理

当端子 A 和 B 短接时,两个电阻便并联连接在各自的电压源两端,此时即可计算流过每个电阻的电流以及总短路电流,具体情况如下:
A–B 短接时
当 A–B 端短路时:
因此,
如果我们将两个电压源短路,并将端子 A 和 B 开路,那么这两个电阻实际上就被并联连接。内部电阻 R_S 的数值通过计算从 A 和 B 端口向内看的总电阻来确定,如下电路所示。
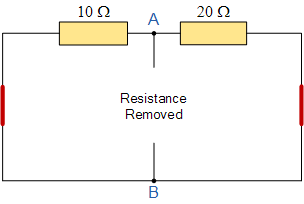
求等效电阻 R_s
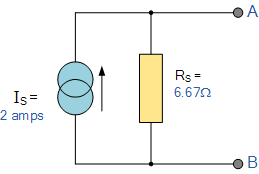
在确定了短路电流 I_S 和等效内部电阻 R_S 后,便得到如下诺顿等效电路。
诺顿定理等效电路
Nortons Theorem Equivalent Circuit
好的,到目前为止都很好,但现在我们必须在端子 A 和 B 之间连接原始的 40\,\Omega 负载电阻并进行求解,如下所示。
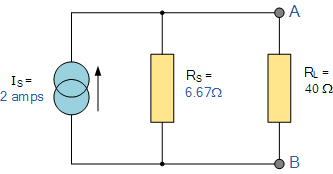
再次,这两个电阻在端子 A 和 B 端并联,其总电阻为:
当负载电阻连接时,端子 A 和 B 之间的电压可表示为:
则流过 40\ \Omega 负载电阻的电流可表示为:
再次使用诺顿定理,可得流过负载电阻 I_3 的电流仍为 I_3 = 0.286\,\mathrm{A},这与前面教程中用基尔霍夫定律计算的结果相同。
诺顿定理总结
我们可以看到,诺顿定理与戴维南定理类似,唯一区别在于:
诺顿等效电路:等效电阻与电流源并联。
戴维南等效电路:等效电阻与电压源串联。
因此,诺顿定理指出:任何线性电网都可以简化为由单个电流源与单个等效电阻并联组成的等效电路。使用诺顿定理求解电路的基本步骤如下:
移除负载电阻 R_L 或相关组件。
将所有电压源短路(或所有电流源开路),测得等效电阻 R_S。
在输出端子 A 和 B 之间短接,测得诺顿电流 I_S。
计算流过负载电阻 R_L 的电流。
在诺顿等效电路中,当负载电阻 R_L 与源电阻 R_S(即电路的等效并联电阻)相等时,负载获得最大功率,即
在下一节教程中,我们将介绍最大功率传输定理。该定理可应用于简单或复杂的线性电路,通过可变负载求得使负载获得最大功率的阻值。
附录
戴维南定理和诺顿定理对比
虽然诺顿等效电路与戴维南等效电路在数学上是完全等价的——只要满足
两者就可互相转换,但在实际工程与分析中,同时保留这两种等效形式有几点好处:
测量与实验方便性不同
若已有电压表可直接测量开路电压 V_{oc},则用戴维南等效更直观;
若已有电流表可直接测量短路电流 I_{sc},则用诺顿等效更简便。
电路类型的“天然匹配”
对于以电压源为主的电路,戴维南形式更符合直观;
对于以电流源或电流控制为主的电路,诺顿形式更贴切。
并联/串联化简更直观
串联电阻适合用戴维南等效,特别是在负载与源串联情况下;
并联电阻适合用诺顿等效,尤其在多个支路并联时候,计算更简洁。
最大功率传输条件表达更加自然
戴维南:最大功率传输时有
R_L = R_{th}诺顿:最大功率传输时有
R_L = R_{N}
两种表达形式完全对偶,但在具体设计时,若是从功率源角度考虑并联分流,用诺顿更直观。
理论与实用的对偶性 诺顿–戴维南对偶性在电路理论中非常重要,保留两种形式不仅能加深对线性网络“串并”对偶关系的理解,也能在不同分析场景中快速选用最简洁的等效模型。
单词表
以下为本次会话中出现的主要英文专业词汇汇总(按字母顺序排列):
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

