戴维南定理
Thevenin’s Theorem
戴维南定理是一种分析方法,用于将复杂电路等效为由一个电压源与一个电阻串联组成的简单电路。
如何在直流分析中使用戴维南定理
How to Use Thevenin’s Theorem For DC Analysis
在之前的三个教程中,我们已经学习了使用基尔霍夫电路定律、网孔分析和节点分析来求解复杂电路。但还有许多“电路分析定理”可供选择,它们能够计算电路中任意节点或支路的电压与电流。在本教程中,我们将学习一种常用的电路分析定理——戴维南定理(仅次于基尔霍夫定律)。
戴维南定理指出:“任何包含多个电压源和电阻的线性电路,都可以等效为一个恒定电压源与一个电阻串联,并与负载相连的二端电路”。换句话说,无论原电路多么复杂,都可以将其简化为一个由恒定电压源 V_{\text{th}} 与等效电阻 R_{\text{th}} 串联,并连接到负载 R_{\text{L}} 两端的二端等效电路,如下所示。
戴维南定理在电力系统、蓄电池系统以及其他互联的纯电阻电路分析中尤为有用,因为它能显著简化对电路相邻部分行为的研究。
戴维南定理等效电路
Thevenins Theorem Equivalent Circuit
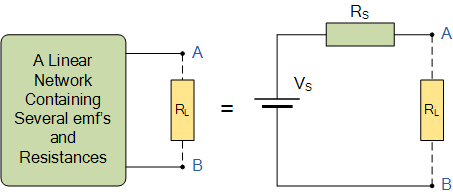
对于负载电阻 R_L 而言,任何由多个电阻电路元件和能量源组成的复杂“一端口”网络,都可以被一个等效电阻 R_s 和一个等效电压 V_s 所替代。 R_s 是从负载端向电路内部看进去时的等效电阻值, V_s 是端口的开路电压。
例如,考虑前面教程中的电路。
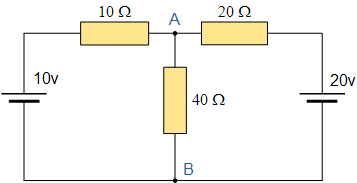
首先,为了分析该电路,我们必须移除连接在端子 A–B 之间的中心 40\:\Omega 负载电阻,并去除与电压源相关的任何内阻。做法是将所有电压源短路(即令 v=0),或将所有电流源开路(即令 i=0)。这样做的原因是我们希望在分析时电路表现为理想电压源或理想电流源。
等效电阻 R_s 的数值,则通过在所有电压源短路后,从端子 A 和 B 向内测量得到的总电阻来确定。这样我们便得到了如下等效电路。
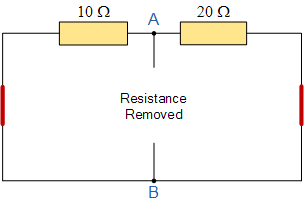
求等效电阻 R_s :
电压 V_s 定义为在端子 A 和 B 之间开路时的总电压。也就是说,在未连接负载电阻 R_L 的情况下。
求等效电压 V_s
Find the Equivalent Voltage (Vs)
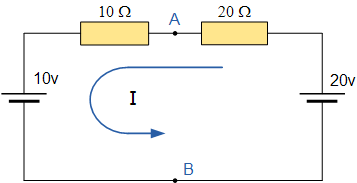
现在我们需要将两个电压源重新接回电路中,并且由于 V_s = V_{AB},环路中流动的电流计算为:
这个 0.33\,\mathrm{A}(330 mA)的电流在两个电阻中是相同的,因此可以分别计算 20\,\Omega 或 10\,\Omega 电阻上的电压降:
或者
因此,戴维南等效电路由一个串联电阻 R_s = 6.67\,\Omega 和一个电压源 V_s = 13.33\,\mathrm{V} 构成。将 40\,\Omega 负载电阻重新接入电路后,我们得到:
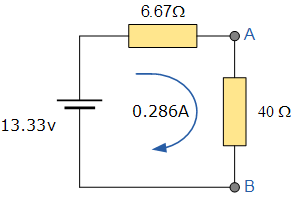
由此,流经电路的电流可表示为:
这个 0.286\mathrm{A} 的电流与我们在前一节使用基尔霍夫电路定律所计算出的值相同。
戴维南定理可以作为另一种电路分析方法,尤为适用于由一个或多个电压源、或电流源与电阻按并联和串联方式互联组成的复杂电路的分析。
虽然戴维南等效电路可用电压与电流的数学关系来描述,但在大规模网络中,其威力不如网孔电流分析或节点电压分析,因为任何一次戴维南化简通常都离不开先用网孔或节点分析来求解,所以不如一开始就直接采用网孔或节点法。然而,戴维南等效在晶体管、电池等电压源电路设计中非常有用。
戴维南定理总结
我们已经看到,戴维南定理是一种将任意复杂电网络简化为由一个电压源 V_s 串联一个电阻 R_s 所构成的简单电路的分析工具。
从端子 A、B 向内看,该简单等效电路在电气特性上与所替换的复杂电路完全相同——即端子 A–B 的 i–v 特性一致。
使用戴维南定理求解电路的基本步骤如下:
移除负载电阻 R_L 或所关心的元件。
将所有电压源短路,或将所有电流源开路,以求得等效电阻 R_s。
使用常规电路分析方法(如网孔或节点分析)求得开路电压 V_s。
重新连接负载电阻 R_L,计算其上流过的电流。
下一节教程中,我们将学习诺顿定理(Norton’s Theorem),它允许将由线性电阻和电源组成的网络等效为一个并联的电流源与一个等效电阻。
附录
为什么是并联而不是串联
看上去两个电阻好像首尾相连,但实际上短路掉两个电压源后,它们的两端都接在同一对端子 A、B 之间,因此它们是并联关系。具体分析如下:
短路电压源
将所有独立电压源内部阻抗视为零,也就是把它们“短路”――电压源两端电位相同。
原来左侧 10 V 电源短路后,10 Ω 电阻的左端直接连到端子 B;
同理,右侧 20 V 电源短路后,20 Ω 电阻的右端也连到端子 B。
连线情况
电阻 10\:\Omega 的两端:一端在 A,另一端在 B;
电阻 20\:\Omega 的两端:一端也在 A,另一端也在 B。 这样,两根电阻的端点都对应到同样的两个节点 A、B,故为并联。
并联计算公式
换言之,哪怕图上它们拉成一条线,只要两端连接的节点相同,就不是“串联”而是“并联”。
电压短路,所以是A,B两点形成新的电源点,电流为开路,则可以理解为电阻无限大,直接断开移除中间的电阻了。
如何判断是内部还是外部
判断“内部”还是“外部”,关键就在于你要简化的二端口(也就是要做戴维南等效的那一对端子)。具体方法如下:
明确端子(Port) 先在原电路中选定两点 A、B——这就是二端口,负载 R_L 原本就接在 A、B 之间。
定义网络边界
外部(External):凡是直接连接在 A–B 端口上的负载元件,都属于“外部”——也就是要从电路中移除,使之开路后再计算内部阻抗。
内部(Internal):除去负载后,其余留在端口 A、B 之外的所有电压源、电流源和电阻网络,都属于“内部”网络。
操作步骤
移除负载:将 R_L 从端子 A–B 处开路(或拔除)。
理想化能量源:所有独立电压源短路、独立电流源开路。
测量阻抗:在此状态下,从 A、B 处“向内看”,测得的总电阻即是等效源阻抗 R_s。
判别要点
如果一个元件在开路 R_L 后仍然留在 A–B 两端的网络中,且参与电流分布或电压分配,它就是“内部”元件。
只有那个被你专门拔掉或开路的 R_L 才是外部。
示意图(虚线框为内部网络, R_L 为外部负载):
┌─────────────────────────┐
────A─│ 内部网络(等效为 Rs) │─B────
└─────────────────────────┘
│
R_L(外部)
│总结:
外部:指定端口上唯一要替换成等效负载的那个元件。
内部:除了外部负载之外,留在端口两端、参与等效电阻计算的所有元件。
戴维南定理与电能质量
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

