串联电感

Inductors in Series

当电感器首尾相连（串联）时，它们共享相同的电流。

这些电感器的相互连接会产生更复杂的网络，其总电感是各个电感值的组合。然而，在串联或并联电感器时，需要遵循某些规则，这些规则基于假设各电感之间不存在互感或磁耦合。

当电感器首尾相接、呈一条直线排列时，称为“串联”。在“串联电阻”教程中我们看到，串联电阻的各阻值可以直接相加，电感也是同样的道理。串联电感的总电感因为线圈匝数实际上被加大，所以各个电感值可直接相加，总电路电感 L_T 等于所有单个电感之和：

串联电感电路图

Inductor in Series Circuit

流过第一个电感器 L_1 的电流 I 别无去处，只能依次通过第二个电感器 L_2、第三个电感器 L_3 等。因此，串联电感具有公共电流，例如：

在上图示例中，电感器 L_1、L_2 和 L_3 首尾相连，连接在 A 点和 B 点之间。由基尔霍夫电压定律（KVL）可知，总电压等于各电感两端电压之和：

而自感电动势由下式给出：

将各电感两端电压代入，可得：

两边同时除以 \tfrac{di}{dt} 后，得出串联电感的总电感表达式：

也就是说，当多个电感串联（且彼此之间无互感或磁耦合）时，总电感等于各电感之和。

要点：串联电路中，任意两个或更多电感器的等效电感 L_T 总是大于串联中最大单个电感的数值。

串联电感示例 1

三个电感器的自感分别为 10\,\mathrm{mH}、40\,\mathrm{mH} 和 50\,\mathrm{mH}，在彼此之间无互感的情况下串联。求该串联组合的总电感：

互联串联电感

Mutually Connected Inductors in Series

当电感器以串联方式连接，并且一个线圈的磁场与另一个线圈发生耦合时，互感的作用会根据磁耦合的程度而增大或减小总电感。互感的影响取决于线圈之间的距离及它们的相对取向。

互联的串联电感可分为“助磁”或“抗磁”两类：

• 助磁耦合（Aiding）：当电流产生的磁通在各线圈中以相同方向通过时，称为累加耦合（Cumulatively Coupled）。

• 抗磁耦合（Opposing）：当电流在各线圈中以相反方向流过时，称为差动耦合（Differentially Coupled）。

累加耦合串联电感

Cumulatively Coupled Series Inductors

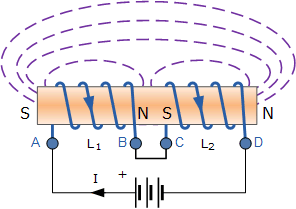
当流经点 A 和 D 之间的两个累加耦合线圈的电流方向相同，上式需要加上互感项以反映两线圈之间的相互作用。各自的自感 L_1 和 L_2 保持不变，互感用 M 表示，则总电动势为：

其中， 2M 表示线圈 L_1 对 L_2 的影响以及 L_2 对 L_1 的影响之和。

两边同时除以 \tfrac{di}{dt}，得累加耦合串联电感的等效电感表达式：

差动耦合串联电感

Differentially Coupled Series Inductors

如果将其中一个线圈翻转，使得同一电流在两线圈中流动方向相反，则互感 M 对各线圈产生抵消作用，称为差动耦合。

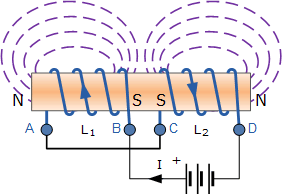
由线圈 2 的互感对线圈 1 产生的电动势与线圈 1 的自感电动势方向相反，因为相同的电流以相反方向通过每个线圈。为考虑此抵消效应，当两个线圈差动连接时，在互感 M 前加上负号，从而得到计算差动耦合串联电路总电感的最终公式：

然后，互感耦合的串联电感器的最终公式如下：

总电感公式：

示例 2

两个电感器的自感均为 10\,\mathrm{mH}，且磁场相互助耦，互感为 5\,\mathrm{mH}。求该串联组合的总电感：

示例 3

两个串联线圈的自感分别为 20\,\mathrm{mH} 和 60\,\mathrm{mH}。该组合的总电感测得为 100\,\mathrm{mH}。假设为累加耦合（助磁）连接，求两线圈之间的互感 M。

由串联耦合电感通用公式：

代入数值：

教程总结

我们现在知道，可以将电感器串联连接，以产生总电感值

其等于各自电感值的和，类似于串联电阻时各阻值相加。然而，电感器相互连接时会受到互感的影响。

互联串联电感根据线圈是累加耦合（同向）还是差动耦合（反向），可分为“助磁”或“抗磁”两类。

在下一篇关于电感器的教程中，我们将看到，在并联连接电感器时，线圈的位置也会影响电路的总电感 L_T。

附录

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。