互感

Mutual Inductance

互感是一个线圈的磁场作用于另一个线圈并在相邻线圈中感应出电压的现象。

互感是两个磁耦合线圈之间的电路参数，定义为一个线圈产生的时变磁通量被感应到邻近第二个线圈中的比率。

之前我们看到，当电感器中的电流变化时，其自身线圈周围变化的磁场会产生自感电动势。当该电动势在产生变化电流的同一回路中产生时，称为自感Self-induction（符号为 L）。

然而，当电动势感应到处于同一磁场内的相邻线圈时，这种电动势称为磁感应、电感或互感，符号为 M。当两个或多个线圈通过公共磁通相互连接时，它们就具有互感特性。

互感是变压器、电动机、发电机以及任何与另一个磁场相互作用的电气元件的基本工作原理。互感可定义为：一个线圈中的电流在相邻线圈中感应电压的能力。

但互感也可能带来不利影响，线圈的“杂散”或“漏”电感可能通过电磁感应干扰相邻元件的正常工作，因此可能需要将其接地屏蔽。

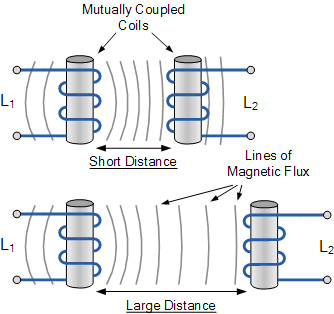
两个线圈之间互感量的大小取决于它们的相对位置。如果两个线圈靠得很近，则第一个线圈产生的几乎全部磁通都会作用于第二个线圈的匝数，从而在第二线圈中感应出较大的电动势，表现为较大的互感值。

反之，如果两线圈相距较远或角度不同，第一个线圈向第二个线圈感应的磁通量就会减弱，产生较小的电动势，因而互感值也较小。因此，互感效应很大程度上取决于两个线圈的相对位置或间距 S，如下图所示。

线圈间互感

Mutual Inductance between Coils

两个线圈之间的互感可以通过将它们置于公共软铁磁心上或增加任一线圈的匝数来大大增大，例如在变压器中常见的做法。

如果两线圈紧密地同绕于同一软铁磁心上，则称它们之间存在“单位耦合”（unity coupling），此时由于磁通泄漏极小，可近似认为磁通完全耦合。假设两线圈之间磁通耦合完美，则它们之间的互感可表示为：

其中：

• \mu_0 为真空磁导率， \displaystyle \mu_0 = 4\pi \times 10^{-7}\,\mathrm{H/m}

• \mu_r 为软铁磁心的相对磁导率

• N_1 和 N_2 分别为两线圈的匝数

• A 为磁心的横截面积，单位为 \mathrm{m}^2

• \ell 为线圈磁路长度，单位为 \mathrm{m}

互感

Mutual Induction

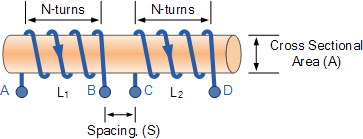
当线圈一（自感量为 L_1）中的电流 I_1 在自身周围建立起磁场，其中一部分磁力线穿过线圈二（自感量为 L_2），在其上感应出电动势，这就是互感。线圈一的匝数为 N_1，线圈二的匝数为 N_2。因此，线圈二相对于线圈一的互感 M_{12} 与它们的相对位置有关，其定义为：

同理，当电流流经线圈二，在其周围产生的磁通穿过线圈一时，线圈一相对于线圈二的互感定义为 M_{21}。由于两者的磁耦合关系相同，我们有

而单个线圈的自感量则由下式给出：

通过对上述式子交叉相乘，可将两线圈之间的互感用它们各自的自感量表示为：

因此，互感的常用表达式为：

需要注意的是，上述推导假设零磁通泄漏、理想 100% 耦合。在实际中，由于磁通泄漏和位置因素的影响，线圈间的耦合系数 k 永远无法达到或超过 1，但在一些特殊设计的磁耦合线圈中可以非常接近 1。

如果仅有部分总磁通耦合到两线圈上，则该耦合部分占总可能耦合磁通的比例称为耦合系数coefficient of coupling，记作 k。

耦合系数

Coupling Coefficient

通常，两个线圈之间的感应耦合量用介于 0 和 1 之间的分数表示，而不是百分比，其中 0 表示无感应耦合，1 表示完全感应耦合。

换句话说，若

则 \textcolor{green}{两线圈完美耦合}；若

则称 \textcolor{red}{两线圈紧密耦合}；若

则称 \textcolor{pink}{两线圈松散耦合}。

在假设理想耦合（k=1）的方程基础上，引入耦合系数 k 后，互感公式可修正为：

当耦合系数 k=1（单位耦合）时，即一个线圈的所有磁力线都穿过第二个线圈的所有匝数，两个线圈紧密耦合，则互感等于两线圈自感量的几何平均值：

此外，当两线圈的电感相等（L_1 = L_2 = L）时，互感等于单个线圈的自感量，因为两个相等值的几何平均等于该值本身：

互感示例 1

两个自感量分别为 75\,\mathrm{mH} 和 55\,\mathrm{mH} 的电感器，放置在同一磁芯上，使得第一线圈产生的 75% 的磁力线切割第二线圈。计算两线圈之间的互感量：

互感示例 2

当两个自感量分别为 5\,\mathrm{H} 和 4\,\mathrm{H} 的线圈均匀绕制在非磁性磁芯上时，测得它们的互感量为 1.5\,\mathrm{H}。计算它们之间的耦合系数：

在下一教程中，我们将探讨将电感器串联连接时对电路互感、总电感及所感应电压的影响。

附录

自耦线圈耦合因素

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。