线圈的电感
Inductance of a Coil
电感(Inductance)是用来描述元件抵抗电流变化的特性名称,即使是一段直导线也会具有一定的电感。
线圈的电感指的是该感性线圈为了抵抗电流变化而呈现出的电气特性。因此,电感只在电路中电流发生变化时才存在。
由于线圈内部磁场的变化,电感器会在自身内部产生自感电动势(emf)。在同一电路中,当电流变化时感应电动势也在该电路内产生,这种现象称为自感(Self-induction),通常用符号 L 表示,有时也称为反电动势(back-emf),因为其极性与外加电压方向相反。
当电动势感应到处于同一磁场内的相邻元件中时,这种现象称为互感(Mutual-induction),用符号 M 表示。互感是变压器、电动机、继电器等设备的基本工作原理。自感是互感的一种特例,由于它产生于单一的独立电路中,我们通常将自感简称为电感。
电感的基本计量单位是亨利(Henry,简写为 \mathrm{H}),以约瑟夫·亨利(Joseph Henry)命名;等价地,它也可表示为韦伯每安培:
楞次定律(Lenz’s Law)指出,感应电动势所产生的电流方向总是反抗引起该电动势的磁通变化——这正是作用与反作用原理。因此,我们可以精确定义电感:
当线圈中电流变化率为 1\,\mathrm{A/s} 时,若在该线圈中感应出 1\,\mathrm{V} 的电动势,则该线圈的电感值为 1\,\mathrm{H}。
换句话说,当通过线圈的电流以每秒 1\,\mathrm{A} 的速率变化时,线圈的电感 L 为 1\,\mathrm{H},这会在其两端感应出 1\,\mathrm{V} 的电压 V_L。因此,表示线圈中电流随时间变化率的数学表达式为:
其中, \mathrm{d}i 表示电流的变化量(单位: \mathrm{A}), \mathrm{d}t 表示电流变化所用的时间(单位: \mathrm{s})。由此,在具有电感 L(单位: \mathrm{H})的线圈中,这一变化所感应出的电压 V_L 可表示为:
负号表示感应电压的方向总是抵抗线圈中电流的变化(\mathrm{d}i/\mathrm{d}t)。
从上述方程,可将线圈的电感表述为:
Inductance of a Coil
其中:
L 为电感,单位为亨利(\mathrm{H});
V_L 为线圈两端的电压;
\mathrm{d}i/\mathrm{d}t 为电流的变化率,单位为安培每秒(\mathrm{A/s})。
电感 L 实际上是感抗电流变化的“阻力”度量,其值越大,对电流变化的抑制越强。
我们知道,感应器件可以将能量以磁场形式储存。感应线圈是由多匝导线组成的,当匝数 N 增加时,在相同电流 I 下,磁通 \Phi 也会增大,因此线圈的电感随之增大。
对于一个简单的单层线圈,其自感可表示为:
Self Inductance of a Coil
其中:
N 为线圈匝数;
\Phi 为每匝的磁通;
I 为流过线圈的电流,单位为安培(\mathrm{A})。
该表达式等价于“磁通量联结”(N\Phi)除以电流 I。注意,此公式仅适用于线性磁性材料。
电感例题 1
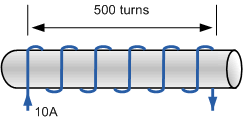
一个空心空气芯电感线圈由 N=500 匝铜线组成,当通过 I=10\ \mathrm{A} 直流电流时,产生的磁通为 \Phi = 10\ \mathrm{mWb} = 0.01\ \mathrm{Wb}.计算该线圈的自感量,单位为毫亨利。
因此,该线圈的自感量为 500\ \mathrm{mH}。
电感例题 2
计算同一线圈在 10 毫秒(10\,\mathrm{ms})时间内所产生的自感电动势。
已知该线圈的自感量为 L = 0.5\,\mathrm{H},假设电流在 10\,\mathrm{ms} 内由 0 变化到 10\,\mathrm{A},则
由自感电动势公式:
因此,该线圈在 10\,\mathrm{ms} 内所产生的自感电动势为 500 V。
线圈的自感系数不仅取决于其结构(尺寸、长度、匝数等),也与材料的磁导率有关。通过使用高磁导率材料和增加匝数,可以获得很高的自感系数。对于内芯为空心的长螺线管,其磁通可表示为:
其中:
\Phi 为磁通;
B 为磁感应强度;
A 为截面积。
当该螺线管单位长度匝数为 N 时,其磁感应强度为:
将上述表达式代入电感的定义式:
约去相同项并整理,得到空气芯螺线管的自感系数:
其中:
L 单位为亨利(\mathrm{H});
\mu_0 为真空磁导率(\mu_0 = 4\pi\times10^{-7}\,\mathrm{H/m});
N 为匝数;
A 为截面积(\mathrm{m}^2);
\ell 为线圈长度(\mathrm{m})。
由于线圈的电感来源于其周围的磁通,对于相同的电流值,磁通越强,电感越大。因此,多匝线圈的电感值要高于少匝线圈。因此,上述电感公式可得电感 L 与匝数的平方成正比:
EEWeb 提供了一个免费的在线线圈电感计算器,可以用于不同线径和线圈布置的电感计算。
除了增加匝数外,我们还可以通过增大线圈直径或延长线圈长度来提高电感。在这两种情况下,制作线圈所需的导线长度都更长,从而产生更多的磁力线以生成所需的反电动势。
如果将线圈绕制在铁磁性芯材(如软铁)上,其电感还可进一步提高,相比于绕制在非铁磁或空气芯上更为明显。

铁氧体磁芯(Ferrite Core)
如果内芯由某种铁磁材料(如软铁、钴或镍)制成,则在相同电流下产生的磁通会大得多,从而大大提高线圈电感。这是因为该材料可以更强烈地集中磁力线通过较软的铁磁芯,如我们在电磁铁教程中所见。
例如,如果芯材的相对磁导率 (\mu_r) 比真空磁导率大 1000 倍,即 \mu_r = 1000,则线圈电感也将增加 1000 倍。因此,我们可以说,线圈电感与芯材的磁导率成正比。
对于绕制在磁芯上的线圈,上述电感公式需引入相对磁导率 \mu_r,修正为:
其中:
\mu_0 为真空磁导率 (4\pi\times10^{-7}\,\mathrm{H/m});
\mu_r 为芯材的相对磁导率;
N 为匝数;
A 为线圈截面积(\mathrm{m}^2);
\ell 为线圈长度(\mathrm{m})。
当线圈绕在铁磁芯上时,随着磁通密度的变化,芯材的磁导率也会变化;对于某些铁磁材料,磁通很快达到饱和,导致电感值呈非线性。因此,由于磁通密度依赖于流过线圈的电流,电感 L 也会成为电流 i 的函数。
在下一节关于电感器的教程中,我们将看到线圈产生的磁场可以使旁边的第二线圈中产生电流,这种现象称为互感(Mutual Inductance),也是变压器、电动机和发电机的基本工作原理。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

