电感器
The Inductor
电感器(Inductor)是一种无源电气元件,由一圈线圈组成,利用电流通过线圈时产生的电—磁相互作用来实现功能。
在本教程中,我们将看到,电感器是用于向电路中引入电感量(inductance)的元件,能够抵抗电流变化(包括大小和方向)。即便是一段直导线,也会具有一定的电感。
在我们的电磁学教程中,已经讨论过当电流通过导线时,其周围会产生磁通。该作用使得磁通方向(围绕导线循环)与电流方向之间存在关系,这便是“弗莱明右手定则”(Fleming’s Right Hand Rule)。
此外,对于绕成线圈的导线,还有另一个重要特性:随着磁通变化(以抵抗电流变化)的运动,在线圈中会感应出次级电压。

A Typical Inductor
在最基本的形式中,电感器不过是绕在中心磁芯上的一圈线。大多数线圈中流过的电流(i)会产生与电流成正比的磁通(N\Phi)。
电感器(又称扼流圈)是一种无源电气元件,由线圈绕制而成,利用流过线圈的电流在自身或其磁芯中产生的磁场来发挥作用。与简单的导线线圈相比,将导线绕制成电感器能够产生更强的磁场。
电感器通常将导线紧密地绕在固体中心磁芯上,磁芯可以是直柱形棒,也可以是连续环形,以集中磁通。
电路图中,电感器的符号就是一组线圈;因此,一圈导线也可以称为电感器。电感器通常根据其内部磁芯类型来分类,例如:空气芯(free air)、实心铁芯(solid iron core)或软磁铁氧体芯(soft ferrite core)。在原理图中,不同磁芯类型可通过在线圈旁边添加实线或虚线平行线来区分。
电感器符号
Inductor Symbol
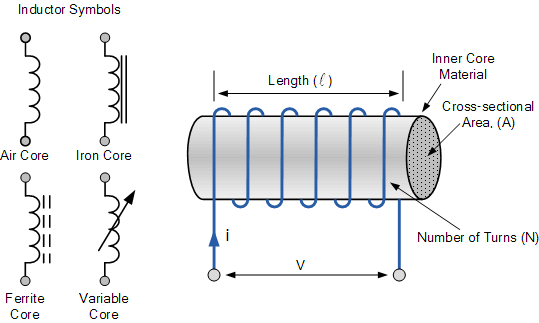
电流 i 流过电感器时,会产生与其成正比的磁通。但与电容器反对其两端电压变化不同,电感器由于其磁场中自感能量的积累,会反对电流大小和方向的变化。
换言之,电感器抵抗电流变化,但对稳态直流电流却几乎没有阻碍。将电流 i 与其磁通联结量 N\Phi 之间的正比关系——即电感器抵抗电流变化的能力——称为电感量,用符号 L 表示,单位为亨利(Henry,简写为 H),以纪念物理学家约瑟夫·亨利(Joseph Henry)。
由于亨利本身是一个相对较大的电感单位,对较小的电感值通常使用亨利的子单位来表示。例如:
因此,为了显示亨利的子单位,我们可以举例:
1\ \mathrm{mH} = 1 毫亨利 —— 等于一亨利的千分之一(1/1\,000)。
100\ \mathrm{\mu H} = 100 微亨利 —— 等于一亨利的一百万分之一(1/1\,000\,000)。
电感器(或线圈)在电气电路中非常常见,其电感值取决于多种因素,例如线圈的形状、绝缘导线的匝数、线层数、匝间距、磁芯材料的磁导率、磁芯的截面积等。
一个电感线圈具有中心磁芯截面积 A,并在线圈长度 \ell 单位长度上保持恒定的匝数。如果一个具有 N 匝的线圈被磁通 \Phi 链接,则该线圈的磁通联结量为 N\Phi
流过线圈的电流 i 会在与电流方向相反的方向上产生感应磁通。根据法拉第电磁感应定律,该磁通联结量的任何变化都会在线圈中产生自感电动势,其表达式为:
其中:
N 是匝数;
A 是磁芯截面积,单位为 \mathrm{m}^2;
\Phi 是磁通量,单位为 韦伯(Wb);
\mu 是磁芯材料的磁导率;
\ell 是线圈的长度,单位为 米(m);
\dfrac{d i}{d t} 是电流变化率,单位为 安培每秒(A/s)。
时变磁场感应出的电压与产生该磁场的电流变化率成正比:正值表示电动势增加,负值表示电动势减少。将常量 \displaystyle \frac{\mu N^2 A}{\ell} 用电感量 L 表示,可得磁通联结量与电流之间的关系:
由于电感器由导电线圈组成,上式可进一步简化,从而得到自感电动势(有时称为线圈中的反向电动势):
电感器产生的反向电动势
Back emf Generated by an Inductor
其中: L 是自感量, \dfrac{\mathrm{d}i}{\mathrm{d}t} 是电流变化率。
因此,从该方程我们可以说——“自感电动势等于电感量乘以电流变化率”。当电路的电感为 1\ \mathrm{H} 且电流以每秒 1\ \mathrm{A/s} 的速率变化时,电路中便会感应出 1\ \mathrm{V} 的电动势。

Inductor Coil
需要注意一点:上述方程仅将电感器两端产生的电动势与电流变化联系起来,因为如果电感电流保持恒定(例如在稳态直流电流中),那么感应电动势将为零——瞬时电流变化率为零,即
当稳态直流电流流过电感器且感应电压为零时,电感器表现得就像一段导线的短路,或者至少呈现出极低的等效电阻。换言之,电感器对电流的阻碍在交流电路和直流电路中有本质的不同。
电感器的时间常数
The Time Constant of an Inductor
我们现在知道,电感器中的电流不可能瞬时变化。因为若要瞬时变化,电流必须在零时间内改变一个有限量,其变化率
将导致无穷大的感应电动势,而无限大的电压在实际中并不存在。但是,如果电感中的电流变化非常迅速(例如开关动作时),就会在线圈两端产生很高的电压。
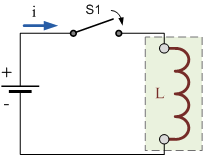
考虑右侧的纯电感电路。当开关(S1)断开时,没有电流流过电感线圈。由于电流为恒定的零值,其变化率也为零:
此时自感电动势
如果在 t=0 时合上开关,电路中将开始有电流流过电感,并以由电感量决定的速率缓慢上升至最大值。根据
此时线圈两端会产生一个与电流变化率成正比的自感电动势,该电动势会“抵抗”外加电压,直到电流达到最大值并进入稳态。进入稳态后,电流的变化率 \tfrac{\mathrm{d}i}{\mathrm{d}t} 为零,线圈的感抗为零,此时电路中的电流仅受线圈直流电阻影响。
同样地,当断开开关(S1)时,线圈中的电流开始下降,电感器会再次通过在相反方向上感应电压来“保持”电流。电流下降的斜率为负,其大小也由电感量决定。
电感器中的电流和电压
Current and Voltage in an Inductor
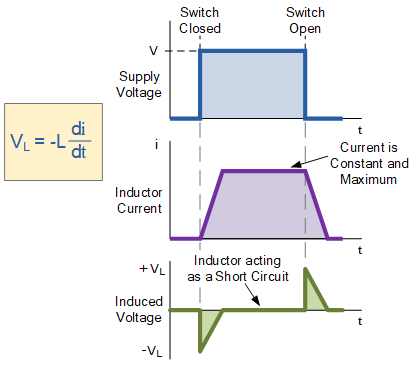
感应电压的大小取决于电流变化率 \displaystyle \frac{\mathrm{d}i}{\mathrm{d}t}。在我们关于电磁感应的教程中,楞次定律指出: \color{red}感应电动势的方向总是反抗引起它的变化 。换句话说,感应电动势总是反对最初引发其产生的运动或变化。
因此,当电流减小时,电压极性表现为电源;当电流增大时,电压极性表现为负载。对于相同的电流变化率 \displaystyle \frac{\mathrm{d}i}{\mathrm{d}t},无论电流是增大还是减小,感应电动势的大小都是相同的。
例题 1
稳态直流电流 4\ \mathrm{A} 通过电感量为 0.5\ \mathrm{H} 的螺线管线圈。若开关闭合后在 10\ \mathrm{ms} 内将电流降至 0\ \mathrm{A},求线圈中产生的平均反电动势。
解答:
根据自感电动势公式:
其中
代入得:
因此,线圈中感应出的平均反电动势大小为
电感器中的功率
Power in an Inductor
我们知道,电路中的电感器会阻碍流经它的电流 i,因为该电流的变化会根据楞次定律在电感器中感应出反向电动势。为了使电流克服此自感电动势持续流动,外部电源必须做功。强迫电流 i 对抗自感电动势 V_L 所消耗的瞬时功率可表示为:
电路中的功率定义为 P = V \times I,因此对于电感器:
对于理想电感器而言,其内部仅具有电感而无直流电阻,即 R=0\ \Omega。因此,线圈内部无任何功率耗散,可认为理想电感器的能量损耗为零。
储存的能量
Energy Stored
当功率流入电感器时,能量便被存储在其磁场中。
当流经电感器的电流增加且 \dfrac{\mathrm{d}i}{\mathrm{d}t}>0 时,瞬时功率 P>0,即有正功率输入,说明能量正被存入电感器中。
同理,当电流减小且 \dfrac{\mathrm{d}i}{\mathrm{d}t}<0 时,瞬时功率 P<0,即有负功率输入,说明电感器正在将能量回馈给电路。
将上述功率表达式对时间积分,可得电感器中总的磁性能量(始终为正值)为:
其中:
W 的单位为焦耳(J),
L 的单位为亨利(H),
i 的单位为安培(A)。
这些能量实际上是由流过电感器的电流在其周围磁场中无损耗地存储起来的。在理想电感器(无电阻、无电容)的情况下,随着电流增加,能量持续存入其磁场;只有当电流减小、磁场崩塌时,能量才被释放回电路。
在交流(AC)电路中,电感器会在每个周期中不断地存储并释放能量;而在直流(DC)电路中,由于电流恒定, \displaystyle P = L\,i\,\frac{\mathrm{d}i}{\mathrm{d}t}=0,储存的能量保持不变。
因此,电感器属于无源元件,它既能存储也能释放能量,但不能自行产生能量。理想电感器被视为无损器件,可无限期地储存能量而无任何损耗。
然而,实际电感器的线圈绕组总会有一定的直流电阻,无论电流是交流还是直流,只要通过电阻就会根据欧姆定律 \bigl(P=I^2R\bigr) 以热量形式损耗能量。
电感器的主要应用包括滤波电路、谐振电路和限流电路。它们可用于阻断或重塑交流信号(不同频率的正弦波),在“调谐”简单无线电接收机或各种振荡器中大放异彩;也可保护敏感设备免受破坏性电压突波和高浪涌电流的冲击。
在下一节关于电感器的教程中,我们将看到线圈的等效阻抗称为“电感”,并且电感这一“抵抗电流变化”的特性,可分为自感(self-inductance)和互感(mutual-inductance)两种形式。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

