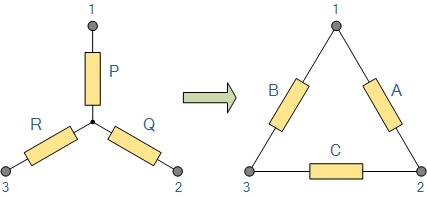
星形-三角形变换 星形—三角形变换(Star-Delta Transformation)和三角形—星形变换(Delta-Star Transformation)允许我们将以三相方式连接的阻抗从一种连接形式转换为另一种形式。
现在,我们可以使用基尔霍夫电路定律(Kirchhoff’s Circuit Laws)、网孔电流分析(Mesh Current Analysis)或节点电压分析(Nodal Voltage Analysis)技术来求解简单的串联、并联或桥式电阻网络。但在平衡三相电路中,我们可以使用星—三角变换技术来简化电路分析,从而减少运算量,这本身就是一件好事。
标准三相电路或网络主要有两种形式,其名称代表了电阻连接的方式:星形(Star)连接网络,用字母 \text{Y} (wye)表示;三角形(Delta)连接网络,用三角形 \Delta (delta)表示。
如果一个三相三线电源或三相负载以其中一种方式连接,则可以通过星—三角变换或三角—星形变换过程将其转换为另一种等效连接。
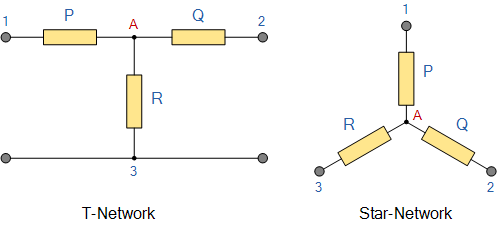
由三个阻抗组成的电阻网络可以连接成一个 \text{T} (Tee) 形配置,但该网络也可以重绘为星形或 \text{Y} 类型网络,如下所示。
T接和等效星形网络 T-connected and Equivalent Star Network
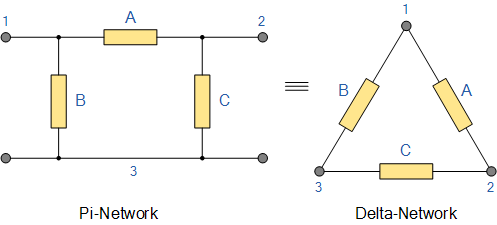
正如我们已经看到的,我们可以将上述 T 型电阻网络重绘为电气上等效的星形或 \text{Y} 型网络。但我们也可以将 Pi 或 \pi 型电阻网络转换为电气上等效的三角形或 \Delta 型网络,如下所示。
\pi 型连接及其等效的 \Delta 型网络 Pi-connected and Equivalent Delta Network
现在我们已经准确定义了星形(Star)和三角形(Delta)连接网络,就可以将 \text{Y} 等效转换为 \Delta 电路,也可以将 \Delta 等效转换为 \text{Y} 电路,使用变换过程。
该过程使我们能够在各电阻之间建立数学关系,从而得出星—三角变换(Star–Delta Transformation)以及三角—星变换(Delta–Star Transformation)的公式。
这些电路变换允许我们将连接的三个电阻(或阻抗)替换为在端子 1\!-\!2、1\!-\!3 或 2\!-\!3 之间测得的等效电阻,无论是星形还是三角形连接电路。
然而,所得网络仅在星形或三角形网络外部对电压和电流等效 ,因为内部的电压和电流是不同的,但每个网络将消耗相同的功率并具有相同的功率因数。
三角-星形变换 Delta Star Transformation
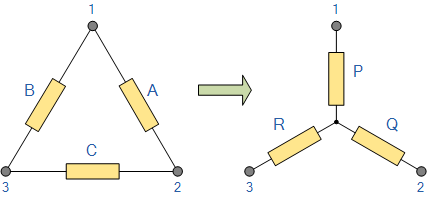
要将三角形网络转换为等效的星形网络,我们需要推导出在各端子之间将各电阻相互等效的变换公式。考虑下图电路。
三角-星形网络 Delta to Star Network
比较端子 1 和 2 之间的电阻。
P + Q = A \text{ in parallel with (B + C)} \\ P + Q = \frac{A\,(B + C)}{A + B + C} \quad\ldots\text{EQ1}
比较端子 2 和 3 之间的电阻。
Q + R = C \text{ in parallel with (A + B)} \\ Q + R = \frac{C\,(A + B)}{A + B + C} \quad\ldots\text{EQ2}
比较端子 1 和 3 之间的电阻。
P + R = B \text{ in parallel with (A + C)} \\ P + R = \frac{B\,(A + C)}{A + B + C} \quad\ldots\text{EQ3}
现在我们得到了三个方程,将方程 3 从方程 2 中相减得到:
\begin{aligned} \text{EQ3} - \text{EQ2} &= (P + R) - (Q + R)\\ P + R &= \frac{B(A + C)}{A + B + C},\quad Q + R = \frac{C(A + B)}{A + B + C}\\ \therefore\;P - Q &= \frac{BA + CB}{A + B + C} - \frac{CA + CB}{A + B + C}\\ &= \frac{BA - CA}{A + B + C} \end{aligned}
然后,重写方程 EQ1 将得到:
P + Q = \frac{AB + AC}{A + B + C}
将方程 EQ1 与上面方程 EQ3 减 EQ2 的结果相加,得到:
\begin{aligned} &(P - Q) + (P + Q) \\ &= \frac{BA - CA}{A + B + C} + \frac{AB + AC}{A + B + C}\\ &= 2P = \frac{2AB}{A + B + C} \end{aligned}
由此我们得到电阻 P 的最终方程为:
P = \frac{AB}{A + B + C}
稍微总结一下上述运算,我们现在可以说:在星形网络中,电阻 P 可以表示为公式 1 加上(公式 3 减去公式 2),即
\text{Eq1} + (\text{Eq3} - \text{Eq2})
类似地,在星形网络中求电阻 Q 时,则是公式 2 加上公式 1 减去公式 3 的结果,即
\text{Eq2} + (\text{Eq1} - \text{Eq3})
由此我们得到电阻 Q 的变换为:
Q = \frac{A C}{A + B + C}.
同样地,在星形网络中求电阻 R 时,是公式 3 加上(公式 2 减去公式 1)的结果,即
\text{Eq3} + (\text{Eq2} - \text{Eq1}),
由此得到电阻 R 的变换为:
R = \frac{B\,C}{A + B + C}.
当将三角形(Δ)网络转换为星形(Y)网络时,所有变换公式的分母都相同:A + B + C,它等于所有Δ电阻之和。要将任意Δ连接网络转换为等效的Y连接网络,我们可以将上述变换公式总结如下:
三角-星形变换方程 \begin{aligned} P &= \frac{A B}{A + B + C},\\ Q &= \frac{A C}{A + B + C},\\ R &= \frac{B C}{A + B + C}. \end{aligned}
如果三角形网络中的三个电阻值都相等,那么等效星形网络中的电阻将等于三角形电阻的三分之一。因此,星形网络中每个电阻分支的值为:
R_{\text{STAR}} = \frac{1}{3}R_{\Delta}
这也就是:
\frac{R_{\Delta}}{3}
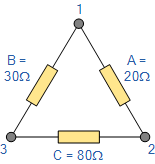
总结例题1 将以下三角形(Δ)电阻网络转换为等效的星形(Y)网络。
Q = \frac{A C}{A + B + C} = \frac{20 \times 80}{130} = 12.31\,\Omega \\ P = \frac{A B}{A + B + C} = \frac{20 \times 30}{130} = 4.61\,\Omega \\ R = \frac{B C}{A + B + C} = \frac{30 \times 80}{130} = 18.46\,\Omega
星-三角形变换 Star Delta Transformation
从星形(Y)网络到三角形( \Delta )网络的变换就是上述过程的逆过程。我们已经看到,当将三角形网络转换为等效的星形网络时,连接到某一端子的电阻等于连接到该端子两条 \Delta 电阻的乘积,例如端子 1 的电阻
P = A \times B
其中 A 和 B 是连接到端子 1 的两条 \Delta 电阻。
通过对之前的公式稍作改写,我们也可以得到将电阻星形网络转换为等效三角形网络的变换公式,从而以如下方式给出所需的变换。
星形-三角形变换 Star to Delta Transformation
三角形( \Delta )网络任意一侧的电阻值,等于星形( \text{Y} )网络中所有两两电阻乘积之和,再除以位于所求三角形电阻“正对面”的星形电阻。例如,对于电阻 A,有:
A = \frac{P\,Q + Q\,R + R\,P}{R}
相对于端子 3,电阻 B 的表达式为:
B = \frac{P\,Q + Q\,R + R\,P}{Q}
相对于端子 2,电阻 C 的变换公式为:
C = \frac{P\,Q + Q\,R + R\,P}{P}
相对于端子 1。
将每个方程除以其分母之后,我们最终得到三个独立的变换公式,可用于将任意三角形(Δ)电阻网络转换为等效的星形(Y)网络,如下所示。
星形-三角变换方程 Star Delta Transformation Equations
\begin{aligned} A &= \frac{P\,Q}{R} + P + Q,\\ B &= \frac{P\,R}{Q} + P + R,\\ C &= \frac{Q\,R}{P} + Q + R. \end{aligned}
最后一点,关于将星形连接的电阻网络转换为等效的三角形连接网络。如果星形网络中的所有电阻值都相等,则等效三角形网络中的电阻值均为星形电阻值的三倍,即:
R_{\Delta} = 3 \times R_{\text{Y}}
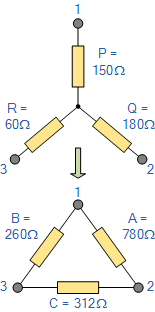
总结例题2 将下列星形( \text{Y} )电阻网络转换为等效的三角形( \Delta )网络。
A = \frac{Q\,P}{R} + Q + P = \frac{180 \times 150}{60} + 180 + 150 = 780\,\Omega
\\
B = \frac{R\,P}{Q} + R + P = \frac{60 \times 150}{180} + 60 + 150 = 260\,\Omega
\\
C = \frac{Q\,R}{P} + Q + R = \frac{180 \times 60}{150} + 180 + 60 = 312\,\Omega
星—三角形变换和三角—星形变换都允许我们将一种连接类型转换为另一种连接类型,从而更方便地分析电路。这些变换技术对于包含电阻或阻抗的星形或三角形电路都能很好地应用。
附录 三角和星形接法对比 特性
星形接线(Y 接)
三角形接线(\Delta 接)
符号
Y
\Delta
中性点
存在中性点,可接地
无中性点,通常不接地
相电压
U_{\text{相–中性}} = \dfrac{U_{\text{线–线}}}{\sqrt3}
U_{\text{相}} = U_{\text{线–线}}
线电压
U_{\text{线–线}} = \sqrt3\,U_{\text{相–中性}}
U_{\text{线–线}} = U_{\text{相}}
线电流
I_{\text{线}} = I_{\text{相}}
I_{\text{线}} = \sqrt3\,I_{\text{相}}
单相负载
可直接使用线–中性电压(如220 V)供单相负载
无中性线,不适合单相负载
典型应用
低压配电、住宅及商业照明、变压器低压侧
三相异步电动机、大功率工业配电、变压器高压侧
短路故障
中性点接地可限制零序电流
三相短路电流在Δ 回路内循环
谐波处理
零序谐波电流流向地网
三次谐波在Δ 回路内自补偿
单词表 英文单词
中文翻译
Star
星形
Delta
三角形
Transformation
变换
Star–Delta Transformation
星—三角形变换
Delta–Star Transformation
三角—星形变换
Kirchhoff’s Circuit Laws
基尔霍夫电路定律
Mesh Current Analysis
网孔电流分析
Nodal Voltage Analysis
节点电压分析
Balanced 3-phase
平衡三相
3-phase
三相
3-wire supply
三线电源
Load
负载
Resistive network
电阻网络
Impedance
阻抗
Series
串联
Parallel
并联
Bridge type
桥式
Tee configuration
T 型结构
Wye (Y)
Y(星形)
Pi (π) network
π 型网络
Equivalent
等效的
Terminals
端子
Resistor
电阻
Equation
方程
Sum
之和
Product
乘积
Combination
组合
Denominator
分母
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。