并联电感器
Inductors in Parallel
当两个或多个电感器的两端分别互相连接时,即称它们为并联连接。并联电感器上的电压降相同,因此,并联电感器具有公共电压。在下例中,电感器两端的电压表示为:
在下图电路中,电感器 L_1、L_2 和 L_3 全部并联连接在 A 点和 B 点之间。
Inductors in Parallel Circuit
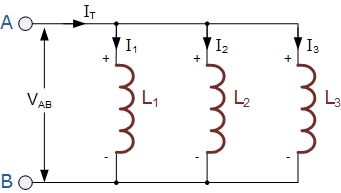
在先前的串联电感教程中,我们了解到电路的总电感 L_T 等于各电感之和;而对于并联连接的电感,等效电感 L_T 的计算方式不同。
根据基尔霍夫电流定律(KCL),并联电感器中流过的总电流为
我们又知道,自感电动势可表示为
将并联组合中流过的总电流 i = i_1 + i_2 + i_3 代入上述表达式,得到并联组合两端的电压为
又将 \displaystyle \frac{d i}{d t} = \frac{v}{L} 代入,可得
进一步化简,可得并联电感器的等效电感公式:
这里,就像并联电阻的计算一样,单个电感的倒数(\tfrac{1}{L_n})值相加,而不是它们本身。但同样地,与串联电感一样,上述公式仅在两个或多个电感之间没有互感或磁耦合(即它们相互磁隔离)时才成立。如果线圈之间存在耦合,总电感还会受到耦合程度的影响。
该计算方法可用于计算单个并联网络中任意数量电感器的总电感。但如果只有两个电感器并联,则可以使用更简单、更快速的公式来求总电感值,即:
关于并联电感电路,有一点很重要:任何两个或多个电感器并联时,其总电感(L_T)总是小于并联支路中最小电感的数值。
教程例题No.1
三个电感器分别为 60\,\mathrm{mH}、120\,\mathrm{mH} 和 75\,\mathrm{mH},在它们之间不存在任何互感,且三者并联连接。求该并联组合的总电感值(以毫亨为单位)。
解: 并联电感的等效电感满足
因此,
互感并联电感器
Mutually Coupled Parallel Inductors
当电感器以并联方式连接,并且其中一个电感的磁场与另一个电感相互连结时,互感的作用会根据线圈之间的磁耦合程度而使总电感值增加或减少。此互感效应取决于线圈之间的距离以及它们的相对取向。
互感并联电感器可分为“助磁”或“抗磁”两种方式:
并联助磁:与无互感时相比,增大等效总电感。
并联抗磁:与无互感时相比,减小等效总电感。
可通过在线圈图示上使用极性点(polarity dots)或极性标记来表示助磁或抗磁的连接方式,如下所示。
并联助磁电感器
Parallel Aiding Inductors
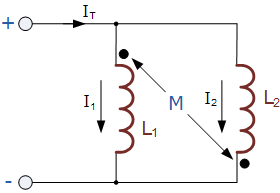
上图中两只并联助磁电感器两端的电压相同,因此电流 i_1 和 i_2 会变化以保持电压相等。于是,两只并联助磁电感器的总电感 L_T 表示为:
其中, 2M 表示线圈 L_1 对 L_2 以及线圈 L_2 对 L_1 的相互影响。
若两只电感相等且磁耦合完全(例如在环形磁芯电路中),则
L_T = L_1 = L_2 = M.若互感为零,则总电感退化为无互感情况下的并联值,即
L_T = \frac{L}{2}.
并联抗磁电感器
Parallel Opposing Inductors
若将其中一只线圈翻转,则得到并联抗磁电感器,此时两线圈之间的互感 M 对各自电感产生抵消作用,而非助磁,如下所示。
然后,两只并联抗磁电感器的总电感 L_T 表示为:
这时,如果两只电感值相等且它们之间的磁耦合完全,则等效电感和电感器上的自感电动势都将为零,因为两只电感互相抵消。
这是因为当电流 i_1 和 i_2 分别流过每只电感时,二者产生的互感磁通在大小相等但方向相反的情况下相互抵消,总互感磁通为零。
因此,这两只线圈对电路中的电流流动等效于短路,所以等效电感 L_T 变为
教程例题 No.2
两个电感器的自感分别为 75\,\mathrm{mH} 和 55\,\mathrm{mH},以助磁并联方式连接。它们的互感为 22.5\,\mathrm{mH}。求并联组合的总电感 L_T。
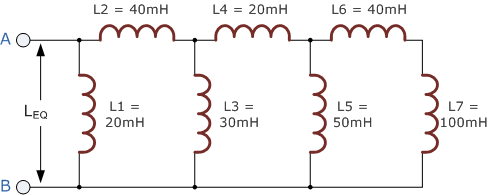
教程例题 No.3
计算如下电感电路的等效电感:
计算第一个电感支路 L_A(电感器 L_5 与电感器 L_6 和 L_7 并联)
L_A \;=\;\frac{L_5\times(L_6+L_7)}{L_5+L_6+L_7} =\frac{50\,\mathrm{mH}\times(40\,\mathrm{mH}+100\,\mathrm{mH})}{50\,\mathrm{mH}+40\,\mathrm{mH}+100\,\mathrm{mH}} =36.8\,\mathrm{mH}.计算第二个电感支路 L_B(电感器 L_3 与电感器 L_4 和 L_A 并联)
L_B \;=\;\frac{L_3\times(L_4+L_A)}{L_3+L_4+L_A} =\frac{30\,\mathrm{mH}\times(20\,\mathrm{mH}+36.8\,\mathrm{mH})}{30\,\mathrm{mH}+20\,\mathrm{mH}+36.8\,\mathrm{mH}} =19.6\,\mathrm{mH}.计算等效电路电感 L_{EQ}(电感器 L_1 与电感器 L_2 和 L_B 并联)
L_{EQ} \;=\;\frac{L_1\times(L_2+L_B)}{L_1+L_2+L_B} =\frac{20\,\mathrm{mH}\times(40\,\mathrm{mH}+19.6\,\mathrm{mH})}{20\,\mathrm{mH}+40\,\mathrm{mH}+19.6\,\mathrm{mH}} =15\,\mathrm{mH}.
最后得到该电路的等效电感为 15\,\mathrm{mH}。
教程小结
与电阻相似,并联连接的电感器两端电压相同,记作 V。并联电感会降低电路的等效电感,若将 N 个电感并联,则等效电感 L_T 为各电感倒数之和的倒数:
L_T \;=\; \Bigl(\sum_{n=1}^{N}\frac{1}{L_n}\Bigr)^{-1}.与串联互感电感器相同,互感并联电感可分为“助磁”或“抗磁”两类,取决于线圈是同向耦合(增加总电感)还是反向耦合(减少总电感)。
到目前为止,我们仅考察了理想的无源电感器。在下一节电感器教程中,我们将研究具有实阻的非理想电感器,其等效电路为电感器与电阻串联,并分析该电路的时间常数。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

