Logo

Menu

张彤
张彤
Published on 2025-09-07 / 10 Visits
0
0

6.LR 串联电路

#电感器

LR 串联电路

LR Series Circuit

所有的线圈、感性器件、扼流圈与变压器在其自身周围都会产生磁场，可将其视为由一个电感（L）与一个电阻（R）串联组成，形成一个 LR 串联电路。

感性线圈与电磁铁（solenoid）并非纯粹的感性器件，而是由一个电感与一个电阻连接在一起，构成一个基本的 LR 串联电路。

在本节关于电感的第一篇教程中，我们曾简要讨论过电感的时间常数，指出流经电感的电流不可能瞬间变化，而是以由感性线圈内部自感反电动势（back-emf）决定的恒定速率增加。

换句话说，电路中的电感会对流过它的电流 i 的变化产生阻碍。虽然这完全正确，但当时我们假设的是理想电感——其线圈绕组不含任何电阻或电容。

然而在现实中，“所有”的线圈——无论是扼流圈、螺线管、电磁继电器，还是任何绕制元件——都会不可避免地具有一定的电阻（无论多小）。这是因为用于绕制线圈的导线（通常为铜线）本身具有电阻值。

因此，出于工程上的实际目的，我们可以把一个简单线圈视为一个“电感” L 与一个“电阻” R 串联。换言之，构成一个 LR 串联电路。

一个 LR 串联电路基本上由一个电感（电感量为 L）与一个电阻（电阻为 R）串联而成。这里的电阻 R 是构成电感线圈的导线匝（或回路）的直流（DC）电阻值。请考虑下图所示的 LR 串联电路。

The LR Series Circuit

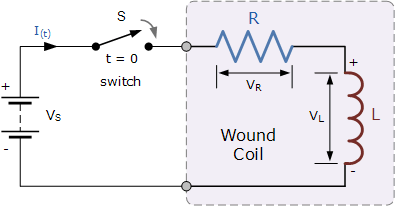
上面的 LR 串联电路接在一个恒定电压源（电池）与一个开关两端。设开关 S 在 t=0 之前保持断开，且在 t=0 闭合后一直保持闭合，从而产生一个“阶跃响应（step response）”类型的电压输入。电流 i 开始在电路中流动，但不会迅速上升到其最大值 I_{\max}，该最大值由欧姆定律中的比值 V/R 决定。

这种受限效应源于电感中自感电动势（由磁通增长产生，楞次定律）的存在。经过一段时间后，电压源对自感电动势的影响被抵消，电流趋于恒定，感生电流与磁场（随时间变化部分）减小为零。

我们可以使用基尔霍夫电压定律（KVL）来表示电路各处的电压降，并据此推导电流的表达式。

KVL 给出：

V(t)-\bigl(V_R+V_L\bigr)=0


电阻 R 上的电压降为（欧姆定律）：

V_R=I\,R


电感 L 上的电压降为我们熟悉的表达式：

V_L=L\,\frac{di}{dt}


于是，该 LR 串联电路各处电压降的最终关系式为：

V(t)=I\,R+L\,\frac{di}{dt}


由此可见，电阻上的电压降取决于电流 i，而电感上的电压降取决于电流变化率 \dfrac{di}{dt}。当 t=0 时电流为零（i=0），上式亦是一阶微分方程，可据此写出任意时刻的电流表达式。

Expression for the Current in an LR Series Circuit

I(t)=\frac{V}{R}\Bigl(1-e^{-Rt/L}\Bigr)\ \ (\mathrm{A})


其中：

  • V 的单位为伏特（\mathrm{V}）；

  • R 的单位为欧姆（\Omega）；

  • L 的单位为亨利（\mathrm{H}）；

  • t 的单位为秒（\mathrm{s}）；

  • e 为自然对数的底数， e \approx 2.71828。

LR 串联电路的时间常数（\tau）为 \displaystyle \tau=\frac{L}{R}，其中 \displaystyle \frac{V}{R} 表示在经历五个时间常数之后的最终稳态电流值。当地流在 5\tau 处达到该最大稳态值时，线圈的电感“好像”已经降为零，更像是一个短路，被有效地从电路中“移除”。

因此，流过线圈的电流仅由线圈绕组的欧姆电阻所限制。电流增长的图形表示（体现电路的电压/时间特性）可表示为：

暂态特性曲线

Transient Characteristics Curves

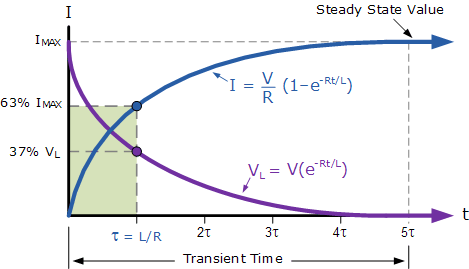
由于电阻上的电压降 V_R 等于 I\cdot R（欧姆定律），它将与电流具有相同的指数增长趋势和曲线形状。然而，电感上的电压降 V_L 将等于： V\,e^{-Rt/L}。因此，在 t=0（或开关刚闭合时），电感两端的电压 V_L 的初值等于电池电压，随后按指数规律衰减至零，如上图曲线所示。

LR 串联电路中电流达到最大稳态值所需的时间大约等于 5 个时间常数，即 5\tau。该时间常数 \tau 以秒为单位，由下式给出： \tau=\frac{L}{R}，其中 R 为电阻的欧姆值， L 为电感的亨利值。这就构成了一个 RL 充电电路的基础，其中 5\tau 也可以理解为 “ 5\cdot(L/R)” 或电路的暂态时间。

任何感性电路的暂态时间由电感与电阻之间的关系决定。例如，在电阻取固定值的情况下，电感越大，暂态时间越慢，因此 LR 串联电路的时间常数越长。同样地，在电感取固定值的情况下，电阻越小，暂态时间越长。

然而，当电感固定时，增大电阻会使暂态时间、也即时间常数变短。这是因为随着电阻增大，电路的电阻性占比越来越高，相比之下电感的作用可忽略不计。如果电阻值相对于电感足够大，则暂态时间将被有效地缩短到几乎为零。

教程示例 No.1

一个线圈的电感为 40\,\mathrm{mH}，电阻为 2\,\Omega，将它们连接成一个 LR 串联电路，并接到 20\,\mathrm{V} 的直流电源上。

a) 电流的最终稳态值为多少？

I=\frac{V}{R}=\frac{20}{2}=10\,\mathrm{A}


b) 该 RL 串联电路的时间常数为多少？

\tau=\frac{L}{R}=\frac{0.04}{2}=0.02\,\mathrm{s}=20\,\mathrm{ms}


c) 该 RL 串联电路的暂态时间为多少？

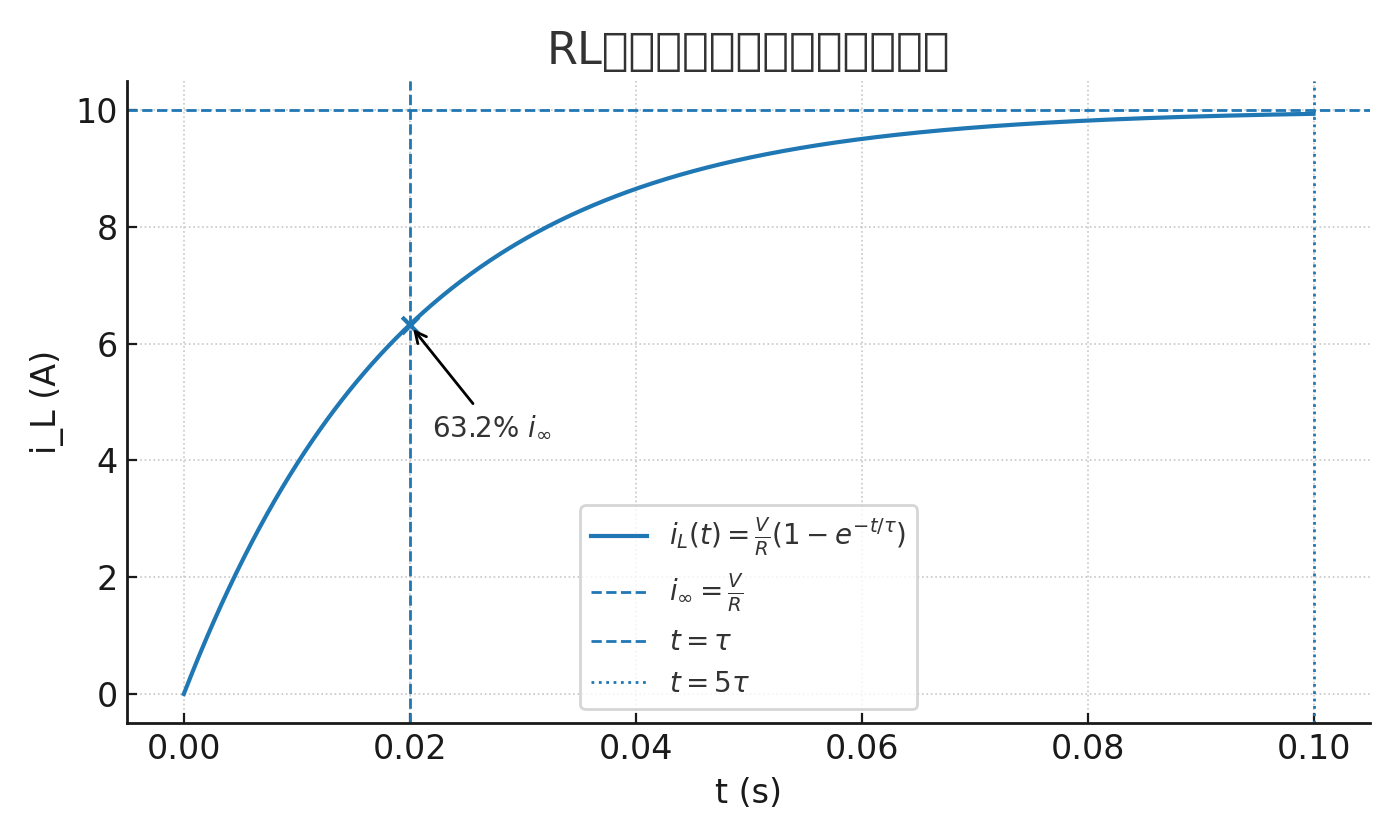
5\tau=5\times 0.02\,\mathrm{s}=100\,\mathrm{ms}


d) 在 10\,\mathrm{ms} 后的感应电动势数值为多少？

V_L=V\,e^{-Rt/L}=20\,e^{-\;2\times 0.01/0.04}

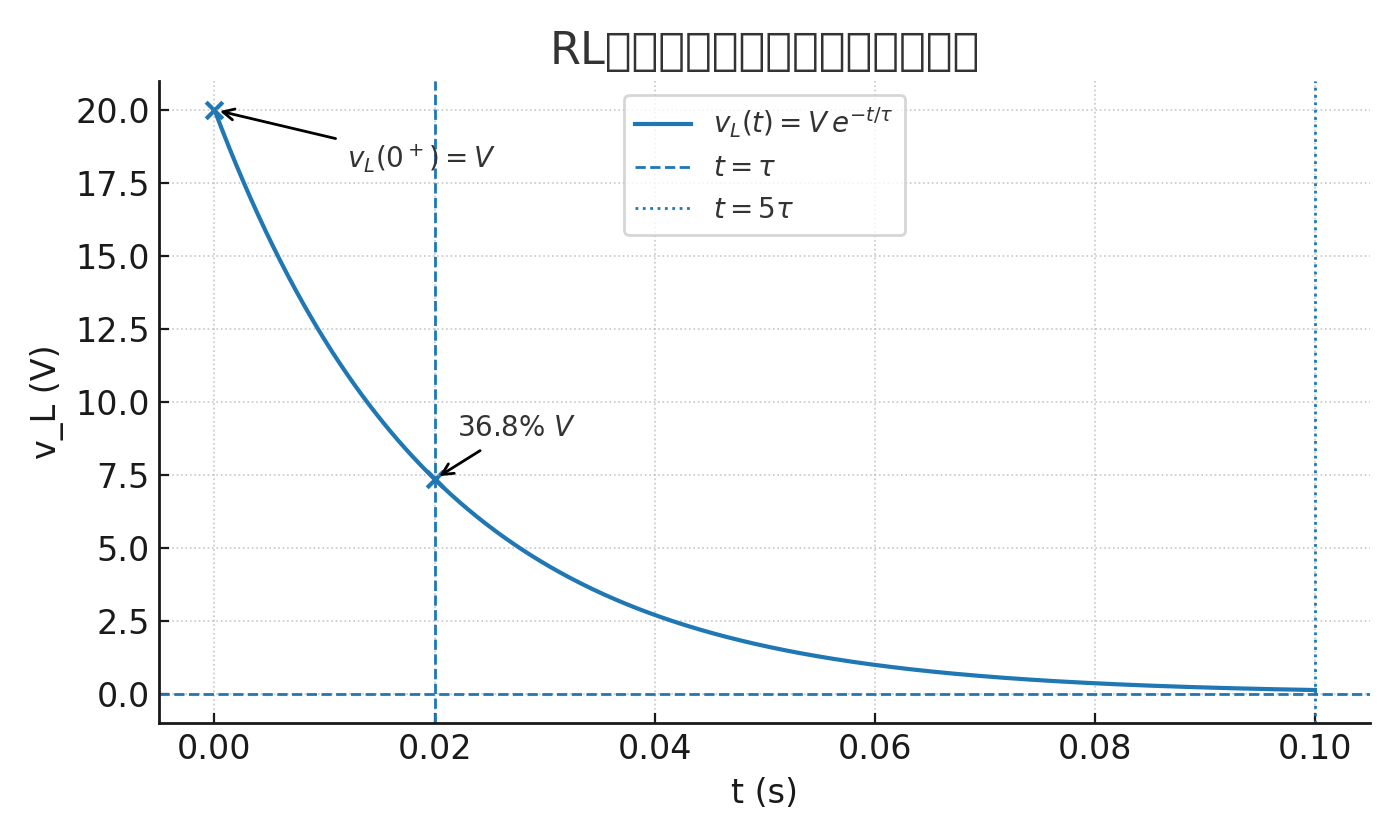
e) 开关闭合后一个时间常数时的电路电流为多少？

I(t)=\frac{V}{R}\Bigl(1-e^{-Rt/L}\Bigr)


该电路的时间常数 \tau 在问题 (b) 中计算为 20\,\mathrm{ms}，于是该时刻的电流如上所示。

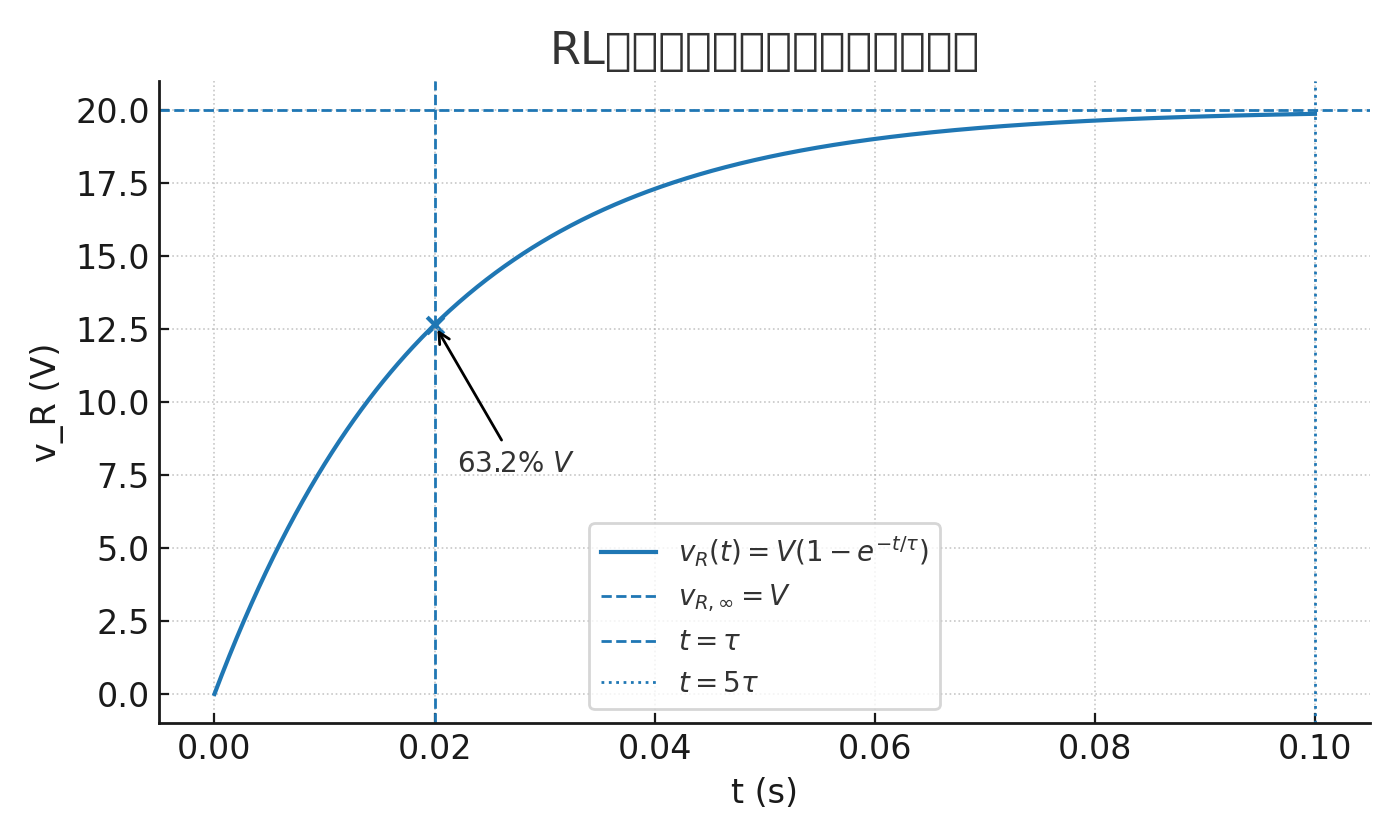
I(t)=\frac{20}{2}\Bigl(1-e^{-2\times 0.02/0.04}\Bigr)


I(t)=10\,(1-0.368)=6.32\,\mathrm{A}


你可能已经注意到，问题 (e) 的答案 6.32\,\mathrm{A}（一个时间常数处）等于最终稳态电流 10\,\mathrm{A} 的 63.2\%。这个 63.2\% 或 0.632\times I_{\max} 的数值也与上面的暂态曲线相对应。

LR 串联电路中的功率

由上可知，电压源向电路提供功率的瞬时速率为：

P = V \times I \quad (\text{W})


电阻以热的形式耗散功率的瞬时速率为：

P = I^{2} R \quad (\text{W})


电感以磁势能形式存储能量的速率为：

P = v\,i \;=\; L\,i\,\frac{di}{dt} \quad (\text{W})


于是，对 RL 串联电路，将电压方程两边同乘以电流 i，可得电路总功率：

P \;=\; i^{2}R \;+\; L\,i\,\frac{di}{dt} \quad (\text{W})


其中，第一项 i^{2}R 表示电阻以热形式耗散的功率，第二项 L\,i\,\dfrac{di}{dt} 表示电感吸收/释放的功率，即其磁能对应的功率项。

附录

LR电路电流表达式推导

下面给出 \displaystyle I(t)=\frac{V}{R}\!\left(1-e^{-Rt/L}\right) 的一步步推导（阶跃电压 V、零初始电流）：

1) 建立微分方程（KVL）

对 LR 串联电路（电阻 R 与电感 L 串联），在 t=0 时刻闭合开关并加上恒定电压 V（单位阶跃），基尔霍夫电压定律给出

V=V_R+V_L=Ri(t)+L\,\frac{di(t)}{dt}.


整理为一阶线性常微分方程：

\frac{di(t)}{dt}+\frac{R}{L}i(t)=\frac{V}{L}.


初始条件：由于电感电流不能突变，且闭合前电路断开，故

i(0)=0.


2) 线性方程通法（积分因子）

积分因子取

\mu(t)=e^{\int (R/L)\,dt}=e^{(R/L)t}.


两边同乘 \mu(t)：

e^{(R/L)t}\frac{di}{dt}+\frac{R}{L}e^{(R/L)t}i =\frac{V}{L}e^{(R/L)t}.


左边是导数的乘积公式：

\frac{d}{dt}\!\Bigl(i(t)\,e^{(R/L)t}\Bigr)=\frac{V}{L}e^{(R/L)t}.


两边从 0 到 t 积分：

i(t)\,e^{(R/L)t}-i(0) =\frac{V}{L}\int_{0}^{t} e^{(R/L)\tau}\,d\tau.


代入 i(0)=0 并计算积分：

\int_{0}^{t} e^{(R/L)\tau}\,d\tau =\frac{L}{R}\Bigl(e^{(R/L)t}-1\Bigr),


故

i(t)\,e^{(R/L)t}=\frac{V}{L}\cdot\frac{L}{R}\Bigl(e^{(R/L)t}-1\Bigr) =\frac{V}{R}\Bigl(e^{(R/L)t}-1\Bigr).


两边同除 e^{(R/L)t}：

i(t)=\frac{V}{R}\Bigl(1-e^{-(R/L)t}\Bigr).


3) 以时间常数表示

定义时间常数 \displaystyle \tau=\frac{L}{R}，则

i(t)=\frac{V}{R}\Bigl(1-e^{-t/\tau}\Bigr).


4) 验证（代回原方程）

\frac{di}{dt}=\frac{V}{R}\cdot\frac{R}{L}\,e^{-Rt/L}=\frac{V}{L}e^{-Rt/L}.


代入 Ri+L\,di/dt：

R\cdot\frac{V}{R}\bigl(1-e^{-Rt/L}\bigr)+L\cdot\frac{V}{L}e^{-Rt/L} =V\bigl(1-e^{-Rt/L}\bigr)+V e^{-Rt/L}=V,


与右端恒压相等，成立；并且 i(0)=0,\ i(\infty)=V/R 符合物理直觉。

扩展（一般初值） 若初始电流为 i(0)=i_0（而非 0），同法可得

i(t)=\frac{V}{R}+\Bigl(i_0-\frac{V}{R}\Bigr)e^{-t/\tau}.


这就是一阶电路的通解形式： 终值 +（初值−终值）\times 指数衰减。

LR电路电流表达式推导（欧拉公式推导）

由 KVL：

L\frac{di}{dt}+Ri=V,\qquad i(0)=0.


1) 齐次解

令 i_h=C\,e^{st}（用欧拉思路，指数是线性常系数方程的本征函数）：

L\,s\,C e^{st}+R\,C e^{st}=0\ \Rightarrow\ Ls+R=0\ \Rightarrow\ s=-\frac{R}{L}.


故

i_h=C\,e^{-\frac{R}{L}t}.


2) 特解

右端为常数，取常数特解 i_p=I_0：

0+R I_0=V\ \Rightarrow\ I_0=\frac{V}{R}.


3) 通解与初值

i(t)=i_h+i_p=\frac{V}{R}+C e^{-\frac{R}{L}t}.


用 i(0)=0 求 C： 0=\frac{V}{R}+C\Rightarrow C=-\frac{V}{R}。 于是

\boxed{\,i(t)=\frac{V}{R}\Bigl(1-e^{-\frac{R}{L}t}\Bigr)\,}.


4) 顺带给出端口电压

v_R(t)=Ri(t)=V\bigl(1-e^{-t/\tau}\bigr),\qquad v_L(t)=L\frac{di}{dt}=V\,e^{-t/\tau},


其中 \tau=\dfrac{L}{R}。

要点：指数函数 e^{st}（由欧拉公式 e^{j\theta}=\cos\theta+j\sin\theta 推广）是线性常系数微分方程的特征解，先解齐次得到衰减指数，再配一个常数特解，最后用初值定系数，过程最短最直观。

电路中的暂态和稳态

（1）概念与术语 “暂态”（transient）是指电路在外部激励或电路拓扑发生突变（如合闸、断开、切换源）后，状态量（电压/电流）由原先工况过渡到新工况的过程；“稳态”（steady state）是指暂态过程结束后的长期状态。对直流激励，稳态常表现为常值；对周期激励（如正弦或周期开关），稳态常表现为周期稳态，即波形按周期 T 重复： x(t+T)=x(t)。

（2）数学表述与分解 在线性时不变（LTI）电路中，任一状态量 x(t) 的解可分解为

x(t)=x_{\text{tran}}(t)+x_{\text{ss}}(t),


其中 x_{\text{tran}}(t) 为自然响应（齐次解），由初始条件与电路极点决定； x_{\text{ss}}(t) 为强迫响应（特解），由外部激励 f(t) 与网络函数决定。常见地，

x_{\text{tran}}(t)=\sum_{k} C_k e^{s_k t},\qquad \Re\{s_k\}<0 \Rightarrow x_{\text{tran}}(t)\to 0,


即当所有极点实部为负时，暂态项指数衰减并最终消失，电路进入稳态。

（3）直流阶跃激励下的典型性质

  • 电容在直流稳态相当于开路：i_C=C\,\dfrac{dv_C}{dt}\to 0。

  • 电感在直流稳态相当于短路：v_L=L\,\dfrac{di_L}{dt}\to 0。 以一阶电路为例： RC 充电（阶跃 V）

v_C(t)=V\!\left(1-e^{-t/(RC)}\right),\qquad i_C(t)=\frac{V}{R}\,e^{-t/(RC)}.


RL 充电（阶跃 V）

i_L(t)=\frac{V}{R}\!\left(1-e^{-t/\tau}\right),\quad v_L(t)=V\,e^{-t/\tau},\quad \tau=\frac{L}{R}.


上式中指数项即为暂态，自然衰减；常值项即为稳态（直流时 \displaystyle i_{L,\infty}=\frac{V}{R}、\displaystyle v_{C,\infty}=V）。

（4）正弦稳态（AC） 若激励为 f(t)=\Re\{F e^{j\omega t}\}，则稳态响应

x_{\text{ss}}(t)=\Re\!\big\{H(j\omega)\,F\,e^{j\omega t}\big\},


幅值与相位由网络函数 H(j\omega) 决定；暂态仍由 e^{s_k t} 给出并随时间消失。正弦稳态分析常用相量法。

（5）时间常数与“ 5\tau”准则 一阶电路的时间常数定义为

\tau_{RC}=RC,\qquad \tau_{RL}=\frac{L}{R}.


在阶跃响应中，偏离终值的误差按 e^{-t/\tau} 衰减：

  • t=\tau 时，尚存 e^{-1}\approx 36.8\% 的误差，即达到终值的 63.2\%；

  • t\approx 5\tau 时，误差 \approx 0.67\%，工程上可视为进入稳态。 高阶系统可用主导极点近似，取 \tau_{\text{dom}}=1/|\Re\{s_{\text{dom}}\}| 估算过渡速度。

（6）工程判据与常见检查

  • 直流稳态判据： L 上 v_L=L\,\dfrac{di}{dt}\approx 0， C 上 i_C=C\,\dfrac{dv}{dt}\approx 0。

  • 周期稳态判据： x(t+T)=x(t)；能量在各周期内收支平衡。

  • 误差阈值法：当 \big|x_{\text{tran}}(t)\big|\le \varepsilon\,\big|x_{\text{ss}}\big|（如 \varepsilon=1\%）即可认为进入稳态，对一阶近似 t\ge \ln(1/\varepsilon)\,\tau。

（7）物理解读与注意事项

  • “电感在稳态等效短路”“电容在稳态等效开路”只适用于直流稳态；在有频率成分或开关边沿存在时， di/dt、 dv/dt 不为零，储能元件仍显著作用。

  • 对固定 L，增大 R 会缩短 \tau=L/R，暂态更快结束；对固定 R，增大 L 会拉长暂态。

本小节给出了暂态与稳态的严格定义、数学分解、典型公式与判据，便于在后续章节中对 RC、RL、RLC 以及周期开关电路进行系统分析与设计。

单词表

English

中文

词性/类别

备注 / 公式（LaTeX）

LR (RL) series circuit

LR（RL）串联电路

n.

V(t)=iR+L\,\dfrac{di}{dt}

inductor

电感（器）

n.

符号 L，单位 \mathrm{H}（henry, 亨利）

inductance

电感量

n.

v_L=L\,\dfrac{di}{dt}

resistor

电阻（器）

n.

符号 R，单位 \Omega

resistance

电阻（值）

n.

v_R=iR

coil / winding

线圈 / 绕组

n.

由导线匝构成，实际有电阻

solenoid

螺线管

n.

一种线圈结构

choke

扼流圈

n.

抑制交流/高频电流

transformer

变压器

n.

由耦合线圈组成

magnetic field

磁场

n.

由电流产生

magnetic flux

磁通

n.

符号 \Phi，单位 \mathrm{Wb}

back emf / self-induced emf

反电动势 / 自感电动势

n.

由 \dfrac{di}{dt} 引起（楞次定律）

Lenz’s law

楞次定律

n.

反抗原因变化的感应极性

Ohm’s law

欧姆定律

n.

v=iR

Kirchhoff’s Voltage Law (KVL)

基尔霍夫电压定律

n.

回路电压代数和为零

step input / step response

阶跃输入 / 阶跃响应

n.

V 在 t=0 突变为常值

time constant

时间常数

n.

\tau=\dfrac{L}{R}（RL 电路）

transient

暂态

n.

自然响应（齐次解），随时间衰减

steady state

稳态

n.

强迫响应（特解）；直流时趋于常值

natural response

自然响应

n.

C e^{-t/\tau} 形式

forced response

强迫响应

n.

由外部激励决定的特解

exponential decay/rise

指数衰减/上升

n.

e^{-t/\tau}；1-e^{-t/\tau}

Euler’s number e

自然对数底 e

n.

e\approx 2.71828

initial condition

初始条件

n.

如 i(0)=0

final value / steady value

终值 / 稳态值

n.

i_\infty=\dfrac{V}{R}

5τ rule

5\tau 准则

n.

约在 t\ge 5\tau 视为稳态

63.2% rule

63.2% 规则

n.

t=\tau 时 1-e^{-1}=63.2\%

voltage across inductor

电感两端电压

n.

v_L(t)=V e^{-t/\tau}（阶跃）

current through inductor

电感电流

n.

i(t)=\dfrac{V}{R}\!\left(1-e^{-t/\tau}\right)

short circuit (DC steady)

（直流稳态）短路

n.

电感于直流稳态等效短路

open circuit (DC steady)

（直流稳态）开路

n.

电容于直流稳态等效开路

power

功率

n.

P=Vi；P=i^2R；P=i^2R+L\,i\,\dfrac{di}{dt}

energy (magnetic)

（磁）能量

n.

W_L=\dfrac{1}{2}Li^2

induced emf

感应电动势

n.

由变化磁通产生

exponential constant

指数常数

n.

与极点/时间常数相关

pole

极点

n.

一阶 RL 的极点 s=-\dfrac{R}{L}

units: volt / ampere / ohm / henry

单位：伏 / 安 / 欧姆 / 亨利

n.

\mathrm{V},\ \mathrm{A},\ \Omega,\ \mathrm{H}

rise time

上升时间

n.

一阶常用 t_r\approx 2.2\tau (10–90%)

transient time

暂态时间

n.

近似取 5\tau

公式总结

序号

公式（LaTeX）

含义（简要）

1

V(t)=i(t)\,R+L\,\dfrac{di(t)}{dt}

KVL：回路电压 = 电阻压降 + 电感感应电压

2

\tau=\dfrac{L}{R}

时间常数，决定响应快慢

3

i(t)=\dfrac{V}{R}\!\left(1-e^{-t/\tau}\right)

阶跃电压、零初值下的电感电流

4

i(t)=\dfrac{V}{R}+\Bigl(i_0-\dfrac{V}{R}\Bigr)e^{-t/\tau}

一般初值的一阶通解

5

v_R(t)=i(t)\,R=V\!\left(1-e^{-t/\tau}\right)

电阻电压的指数上升

6

v_L(t)=L\,\dfrac{di(t)}{dt}=V\,e^{-t/\tau}

电感电压的指数衰减（ t=0^+ 时等于 V）

7

P=V\,i

电源对外瞬时功率

8

P_R=i^2R

电阻耗散功率（热）

9

P_L=L\,i\,\dfrac{di}{dt}

电感吸收/释放功率（磁能变化率）

10

P_{\text{total}}=i^2R+L\,i\,\dfrac{di}{dt}

RL 支路吸收的总瞬时功率

11

W_L=\dfrac{1}{2}L\,i^2

电感磁场储能

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。

5.并联电感器
7.感性电抗

Comment