节点电压分析
Nodal Voltage Analysis
节点电压分析用于求解电路中不同节点之间的未知电压降,这些节点为两个或多个元件提供公共连接点。
节点电压分析与之前的网孔分析互补,二者同样强大,且都基于矩阵分析的基本概念。顾名思义,节点电压分析利用基尔霍夫第一定律的“节点”方程来求解电路中的电压势。
因此,将所有这些节点电压相加,结果为零。若电路中有 n 个节点,则会有 n-1 个独立的节点方程,这些方程足以描述并求解整个电路。
在每个节点处写下基尔霍夫第一定律方程,即“流入节点的电流在数值上等于流出节点的电流”,然后将每个电流用跨支路的电压表示。对于 n 个节点,其中一个节点将作为参考节点,所有其他电压均相对于该公共节点来测量。
例如,考虑前一节中的电路。
节点电压分析电路
Nodal Voltage Analysis Circuit
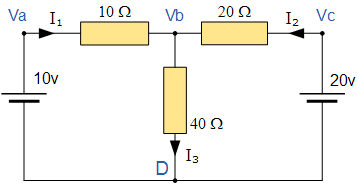
在上述电路中,节点 D 被选为参考节点,其它三个节点相对于节点 D 分别假设具有电压 V_a、V_b 和 V_c。例如:
\frac{V_a - V_b}{10} \;+\;\frac{V_c - V_b}{20} \;=\;\frac{V_b}{40}\,.
基尔霍夫第一定律
由于 V_a = 10\,\mathrm{V} 且 V_c = 20\,\mathrm{V},V_b 可由下式求得:
\left(1 - \frac{V_b}{10}\right) + \left(1 - \frac{V_b}{20}\right) = \frac{V_b}{40}
2 = V_b\Bigl(\frac{1}{40} + \frac{1}{20} + \frac{1}{10}\Bigr)
V_b = \frac{80}{7}\,\mathrm{V}
I_3 = \frac{2}{7}\,\mathrm{A}\ \text{或}\ 0.286\,\mathrm{A}
再次得到相同的 0.286\ \mathrm{A} 值,这与我们在前一节教程中使用基尔霍夫电路定律所求得的结果相同。
从到目前为止我们所讨论的网孔分析和节点电压分析方法来看,这是求解此特定电路最简单的方法。通常,当电路中存在较多电流源时,更适合使用节点电压分析。此时,网络的定义为:
\mathbf{I} = \mathbf{Y}\,\mathbf{V}
其中 \mathbf{I} 是驱动电流源向量, \mathbf{V} 是待求节点电压向量, \mathbf{Y} 是网络的导纳矩阵,其作用于 \mathbf{V} 可得到 \mathbf{I}。
教程小结
求解节点电压分析方程的基本步骤如下:
写出电流向量,假设流入节点的电流为正。即对 N 个独立节点,得到一个 (N\times1) 的电流向量。
写出网络的导纳矩阵 \mathbf{Y},其中:
Y_{11} = \text{第 1 个节点的总导纳}, \\ \quad Y_{22} = \text{第 2 个节点的总导纳}, \\ \quad Y_{JK} = \text{连接节点 }J\text{ 与节点 }K\text{ 的总导纳}.
对于具有 N 个独立节点的网络, \mathbf{Y} 是一个 ( N\times N) 的矩阵,其中 Y_{nn} 为正值, Y_{jk} 为负值或零。
电压向量是一个 ( N\times1) 向量,列出待求的 N 个节点电压。
我们现在已经看到,有若干定理可以简化线性电路的分析。在下一个教程中,我们将学习戴维南定理,该定理允许将由线性电阻和电源组成的网络,用一个包含单一电压源和一个串联电阻的等效电路来表示。
附录
节点电压分析举例
电路描述
参考节点:地(0 V)。
节点 1:有一个 2 A 的电流源注入节点 1,通过电阻 R_1=5\:\Omega 接地。
节点 2:有一个 1 A 的电流源注入节点 2,通过电阻 R_2=20\:\Omega 接地。
节点 1 与节点 2 之间 有一个电阻 R_{12}=10\:\Omega 连接。
1. 写电流向量 \mathbf{I}
\mathbf{I} = \begin{pmatrix} I_1\\[0.3em] I_2 \end{pmatrix} = \begin{pmatrix} 2\\[0.3em] 1 \end{pmatrix} \quad(\mathrm{单位:A})
2. 写导纳矩阵 \mathbf{Y}
Y_{11} = \frac1{R_1} + \frac1{R_{12}} = \frac1{5} + \frac1{10} = 0.2 + 0.1 = 0.3\;\mathrm S,
Y_{22} = \frac1{R_{12}} + \frac1{R_2} = \frac1{10} + \frac1{20} = 0.1 + 0.05 = 0.15\;\mathrm S,
Y_{12} = Y_{21} = -\frac1{R_{12}} = -0.1\;\mathrm S.
所以
\mathbf{Y} = \begin{pmatrix} 0.3 & -0.1\\[0.3em] -0.1 & 0.15 \end{pmatrix}.
3. 写节点电压向量 \mathbf{V}
\mathbf{V} = \begin{pmatrix} V_1\\[0.3em] V_2 \end{pmatrix} \quad(\mathrm{单位:V}).
4. 建立并求解方程 \mathbf{I} = \mathbf{Y}\,\mathbf{V}
\begin{pmatrix} 2\\[0.3em] 1 \end{pmatrix} = \begin{pmatrix} 0.3 & -0.1\\[0.3em] -0.1 & 0.15 \end{pmatrix} \begin{pmatrix} V_1\\[0.3em] V_2 \end{pmatrix}.
对应的标量方程组为:
\begin{cases} 0.3\,V_1 \;-\;0.1\,V_2 = 2,\\[0.4em] -0.1\,V_1 + 0.15\,V_2 = 1. \end{cases}
计算行列式:
\Delta = 0.3\times0.15 \;-\;(-0.1)\times(-0.1) = 0.045 - 0.01 = 0.035.
由克莱姆法则,
V_1 = \frac{ \begin{vmatrix} 2 & -0.1\\[0.3em] 1 & 0.15 \end{vmatrix} }{\Delta} = \frac{2\cdot0.15 - (-0.1)\cdot1}{0.035} = \frac{0.3 + 0.1}{0.035} = \frac{0.4}{0.035} \approx 11.43\;\mathrm V,
V_2 = \frac{ \begin{vmatrix} 0.3 & 2\\[0.3em] -0.1 & 1 \end{vmatrix} }{\Delta} = \frac{0.3\cdot1 - 2\cdot(-0.1)}{0.035} = \frac{0.3 + 0.2}{0.035} = \frac{0.5}{0.035} \approx 14.29\;\mathrm V.
结果:
V_1 \approx 11.43\;\mathrm V,\quad V_2 \approx 14.29\;\mathrm V.
此例完整演示了如何按“\mathbf{I}=[Y][V]”形式搭建方程并求解节点电压。
网孔分析与节点分析
特点 | 网孔分析 | 节点分析 |
|---|
基础定律 | 基尔霍夫第二定律(KVL)——环路电压 | 基尔霍夫第一定律(KCL)——节点电流 |
未知量 | 网孔电流 I_1, I_2, \dots | 节点电压 V_1, V_2, \dots |
方程形式 | \displaystyle \sum_{\text{环路}} V = 0 | \displaystyle \sum_{\text{节点}} I = 0 |
矩阵表达 | [\;R\;]\,[I] = [V] | [\;Y\;]\,[V] = [I] |
适用场景 | 电压源和电阻网络较多,回路数较少时 | 电流源和电阻网络较多,节点数较少时 |
优缺点 | 对含电流源的环路要先做源变换 | 对含电压源的节点要先做源变换 |
单词表
English | 中文 |
|---|
Nodal Analysis | 节点电压分析 |
Mesh Analysis | 网孔电流分析 |
Circuit | 电路 |
Node | 节点 |
Reference Node | 参考节点 |
Voltage | 电压 |
Current | 电流 |
Branch | 支路 |
Voltage Drop | 电压降 |
Potential | 电势 |
Kirchhoff’s First Law | 基尔霍夫第一定律 |
Kirchhoff’s Second Law | 基尔霍夫第二定律 |
KCL (Current Law) | 基尔霍夫电流定律 |
KVL (Voltage Law) | 基尔霍夫电压定律 |
Matrix Analysis | 矩阵分析 |
Admittance | 导纳 |
Resistance | 电阻 |
Admittance Matrix | 导纳矩阵 |
Resistance Matrix | 电阻矩阵 |
Driving Current Source | 驱动电流源 |
Voltage Source | 电压源 |
Current Source | 电流源 |
Independent | 独立的 |
Summation | 求和 |
Solve | 求解 |
Unknown | 未知(量) |
Thevenin’s Theorem | 戴维南定理 |
Equivalent Circuit | 等效电路 |
Series Resistance | 串联电阻 |
Vector | 向量 |
Network | 网络 |
Complement | 互补 |
Tutorial | 教程 |
Summary | 小结 |
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。


