网孔电流分析

Mesh Current Analysis

网孔电流分析（Mesh Current Analysis）是一种用于求解电路中沿闭合路径或网孔内环流电流的技术。

所谓网孔 (mesh)， 指的是电路中的一个独立回路（没有内部包含其他回路的基本回路），通常被想象成一个“网孔”。

虽然基尔霍夫定律（Kirchhoff’s Laws）为分析任意复杂电路提供了基本方法，但通过使用网孔电流分析（Mesh Current Analysis）或节点电压分析（Nodal Voltage Analysis）可以在某些情况下改进这一方法，从而减少所涉及的数学计算量。当涉及大型网络时，这种数学简化就是一个重要优势。

例如，考虑前一节中提到的那个电路实例。

网孔电流分析电路

Mesh Current Analysis Circuit

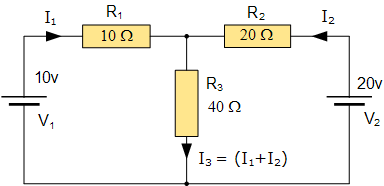
一种简化数学计算的方法是，使用基尔霍夫电流定律（KCL）的方程来分析电路，从而求解流经两个电阻的电流 I_1 和 I_2。这样就无需单独计算电流 I_3，因为它只是 I_1 与 I_2 的总和。

因此，基尔霍夫第二电压定律（KVL）就简化为：

\text{方程一：} \quad 10 = 50I_1 + 40I_2

\text{方程二：} \quad 20 = 40I_1 + 60I_2

由此，节省了一行数学计算。

网孔电流分析

一种更简便的求解上述电路的方法是使用网孔电流分析（Mesh Current Analysis）或回路分析（Loop Analysis），这种方法有时也被称为 麦克斯韦环流法（Maxwell’s Circulating Currents method）。

与标记支路电流不同，这种方法要求我们给每一个闭合回路标记一个环流电流（circulating current）。

一般的经验法则是：仅标记内部的回路，并采用顺时针方向标记环流电流，其目的是确保电路中的每个元件至少被一个回路电流覆盖一次。任何所需的支路电流都可以通过这些合适的网孔或回路电流来计算，就像使用基尔霍夫方法那样。

例如：

i_1 = I_1,\quad i_2 = -I_2,\quad I_3 = I_1 - I_2

接下来我们像之前一样，使用基尔霍夫电压定律（KVL）来列写方程并求解。不过该方法的优势在于：它可以保证从电路方程中获取的是求解电路所需的最少信息量，因为这些信息是更通用的，并且可以方便地写成矩阵形式。

例如，考虑前一节中提到的那个电路：

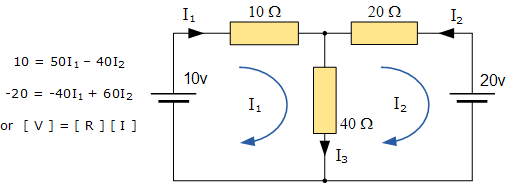
这些方程可以通过使用一个单一网孔阻抗矩阵 Z 来快速求解。这个矩阵中的每个主对角线上的元素都是“正值”，代表各个网孔中阻抗的总和。而每个非主对角线元素则是“零”或“负值”，代表连接相邻网孔的电路元件的阻抗。

首先我们需要理解，在处理矩阵运算时，两个矩阵的相除其实等同于一个矩阵乘以另一个矩阵的逆矩阵。

原始关系式

[V] = [I] \times [R] \quad \text{或} \quad [R] \times [I] = [V]

电路的矩阵表示

\begin{bmatrix} 50 & -40 \\ -40 & 60 \end{bmatrix} \times \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} = \begin{bmatrix} 10 \\ -20 \end{bmatrix}

求解电流向量

I = \frac{V}{R} = R^{-1} \times V

求逆矩阵
\text{Inverse of } R = \begin{bmatrix} 60 & 40 \\ 40 & 50 \end{bmatrix}

行列式计算：
|R| = (60 \times 50) - (40 \times 40) = 1400

进而写出逆矩阵：
\therefore R^{-1} = \frac{1}{1400} \begin{bmatrix} 60 & 40 \\ 40 & 50 \end{bmatrix}

在求得 R 的逆矩阵之后， \dfrac{V}{R} 与 V \times R^{-1} 等价，因此我们现在可以利用它来求出两条环流电流。

矩阵形式求环流电流

[I]=[R^{-1}]\,[V]

\begin{bmatrix} I_1\\ I_2 \end{bmatrix} = \frac{1}{1400} \begin{bmatrix} 60 & 40\\ 40 & 50 \end{bmatrix} \begin{bmatrix} 10\\ -20 \end{bmatrix}

计算：

\begin{aligned} I_1 &= \frac{60\times10 + 40\times(-20)}{1400} = \frac{-200}{1400} = -0.143\;\text{A}\\[6pt] I_2 &= \frac{40\times10 + 50\times(-20)}{1400} = \frac{-600}{1400} = -0.429\;\text{A} \end{aligned}

因此，两条网孔（环路）电流分别为

\boxed{I_1 = -0.143\ \text{A}},\qquad \boxed{I_2 = -0.429\ \text{A}}.

其中:

[V]：依次给出回路 1与回路 2的总电源电压
[I]：列出我们要计算的各回路电流名称
[R]：电阻矩阵
[ R^{-1}]：[R] 的逆矩阵

由此计算得到

I_1 = -0.143\ \text{A}, \qquad I_2 = -0.429\ \text{A}

又因为

I_3 = I_1 - I_2

则

I_3 = -0.143 - (-0.429) = 0.286\ \text{A}

这个 0.286\ \text{A} 的结果与我们在基尔霍夫电路定律教程中先前求得的数值相同。

教程总结

这种“直观观察（look-see）”的电路分析方法大概是所有分析方法中最简便的一种。采用网孔电流分析时，基本的解题步骤如下所示：

给所有内部回路标注环流电流（I_1, I_2, \dots , I_L 等）。
书写 [L \times 1] 列矩阵 \mathbf V，其元素为各回路中所有电压源的代数和。
构造 [L \times L] 电阻矩阵 \mathbf R，规则如下：
- R_{11}：第 1 个回路中的电阻总和；
- R_{nn}：第 n 个回路中的电阻总和；
- R_{jk}：直接连接回路 j 与回路 k 的电阻值（若无连接则为 0）。
写出矩阵方程
\mathbf V = \mathbf R\,\mathbf I

其中 \mathbf I 为待求的电流向量。

按照这个步骤可以参考附录网孔分析逐步分解

除了网孔电流分析外，我们还可以使用节点分析（Nodal Analysis）来求解各节点（或回路）电压，同样只依赖基尔霍夫定律并进一步减少数学运算量。在下一篇直流电路理论教程中，我们将详细介绍节点电压分析（Nodal Voltage Analysis）的具体做法。

附录

网孔电流分析逐步详解示例

下面给出一个两网孔直流电路的完整示例，按前面总结的 4 个步骤（标注环流 → 写 \mathbf V → 写 \mathbf R → 列式求解）一步步演示。

1 电路描述与环流标注

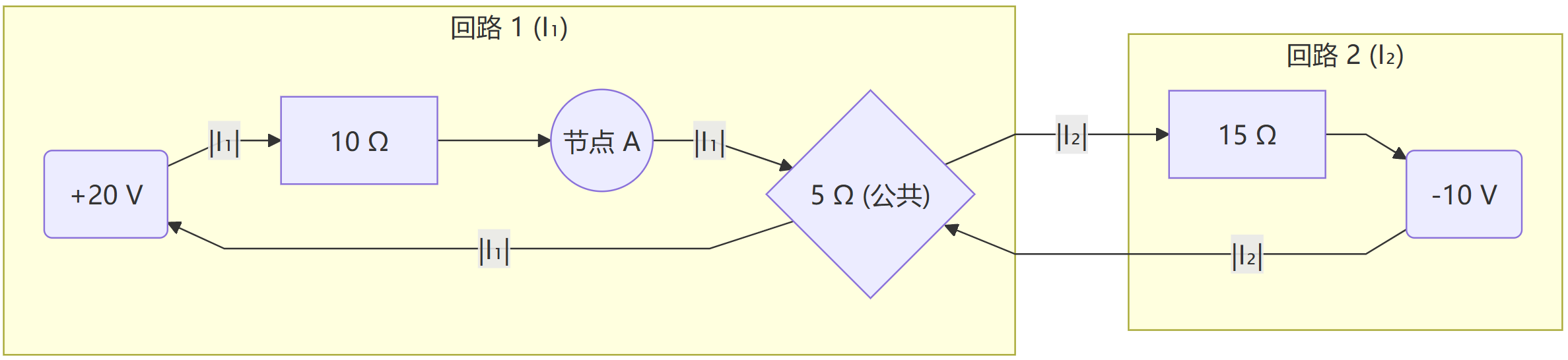
回路 1（右手顺时针）电流： I_1 元件：电源 V_{s1}=+20\text{ V}，电阻 10 Ω，公共电阻 5 Ω
回路 2（同样顺时针）电流： I_2 元件：电源 V_{s2}=-10\text{ V}（符号表示极性与 I_2 方向相反），电阻 15 Ω，公共电阻 5 Ω

2 写出 \mathbf V 列矩阵

\mathbf V = \begin{bmatrix} \;\;+\;20 \\[2pt] -10 \end{bmatrix} \ \text{V}

3 构造电阻矩阵 \mathbf R

R_{11}=10\;Ω+5\;Ω=15\;Ω
R_{22}=15\;Ω+5\;Ω=20\;Ω
R_{12}=R_{21}=-5\;Ω（负号表示两回路共享该 5 Ω 且电流方向相反）

\mathbf R = \begin{bmatrix} 15 & -5 \\ -5 & 20 \end{bmatrix} \;\bigl[\Omega\bigr]

4 列矩阵方程并求解

\mathbf V = \mathbf R\,\mathbf I \quad\Longrightarrow\quad \mathbf I = \mathbf R^{-1}\mathbf V

\begin{bmatrix} 15 & -5 \\ -5 & 20 \end{bmatrix} \begin{bmatrix} I_1\\ I_2 \end{bmatrix} = \begin{bmatrix} 20\\ -10 \end{bmatrix}

计算（手算或借助计算机）： 行列式
\lvert\mathbf R\rvert =15\times20-(-5)\times(-5)=300-25=275

\mathbf R^{-1} =\frac1{275} \begin{bmatrix} \ \ 20 & 5\\ \ \ 5 & 15 \end{bmatrix}

\mathbf I =\frac1{275} \begin{bmatrix} 20 & 5\\ 5 & 15 \end{bmatrix} \!\begin{bmatrix} 20\\[-2pt] -10 \end{bmatrix} = \begin{bmatrix} \displaystyle \tfrac{14}{11}\\[6pt] \displaystyle -\tfrac{2}{11} \end{bmatrix} \text{A}

\boxed{I_1 = 1.273\ \text{A}},\qquad \boxed{I_2 = -0.182\ \text{A}}

正号表示 I_1 与假设方向一致；
负号表示 I_2 实际方向与假设方向相反。

5 求支路电流（公共 5 Ω 电阻）

I_3 = I_1 - I_2 = 1.273\;-\;(-0.182) = 1.455\ \text{A}

要点回顾
先统一环流方向（顺或逆时针都可，保持一致）。
\mathbf V 只放“本回路电压源的代数和”。
\mathbf R 主对角填本回路总阻抗，非对角填“负共享阻抗”。
解 \mathbf I=\mathbf R^{-1}\mathbf V 即得所有网孔电流，再换算所需支路电流、电压。

矩阵形式的欧姆定律

为什么欧姆定律能够“升级”为矩阵形式？

核心结论：只要电路满足 线性元件 + 基尔霍夫两大定律，标量欧姆定律
\displaystyle v = iR

自然推广为
\boxed{\;\mathbf V=\mathbf R\,\mathbf I\;}

或（节点分析时）
\boxed{\;\mathbf G\,\mathbf V=\mathbf I_{\text{注入}}\;}

下面分三步给出“证明思路”与形式化推导（电阻网络为例，电抗元件在稳态交流下同理，只需把 R 换成复阻抗 Z=\!R+jX）。

1. 逐支路欧姆定律 ➜ 逐节点/逐网孔矩阵

1.1 单支路（标量）

v_k \;=\; i_k\,R_k,\qquad k=1,2,\ldots, b

这里 b 是支路数。

1.2 收集成向量

\mathbf v=\begin{bmatrix}v_1\\\vdots\\v_b\end{bmatrix},\; \mathbf i=\begin{bmatrix}i_1\\\vdots\\i_b\end{bmatrix},\; \mathbf R=\operatorname{diag}(R_1,\dots,R_b)

于是

\mathbf v \;=\; \mathbf R\;\mathbf i \tag{1}

这就是矩阵版欧姆定律的最原始形态：对角矩阵只把每条支路自己的 R_k 摆在对角线上。

2. 加入基尔霍夫定律：

2.1 KCL（节点电流定律）

令

\mathbf A\in\mathbb R^{n\times b}

为 节点–支路关联矩阵（入 = +1，出 = –1）；对每个节点 p 有

\sum_{k} A_{pk}\,i_k \;=\; I_p^{\text{注入}}

写成矩阵：

\boxed{\; \mathbf A\,\mathbf i \;=\;\mathbf I_{\text{注入}} \;} \tag{2}

2.2 KVL（回路电压定律）

\mathbf A^{\!\mathsf T}\,\mathbf v \;=\;\mathbf 0 \tag{3}

2.3 联立 (1)(2)(3) 消元

把 (1) 代入 (3)：

\mathbf A^{\!\mathsf T}\,\mathbf R\,\mathbf i \;=\;\mathbf 0

再用 (2) 消去 \mathbf i：

\mathbf A^{\!\mathsf T}\,\mathbf R\,\mathbf A^{+}\,\mathbf I_{\text{注入}} \;=\;\mathbf 0

（ \mathbf A^{+} 表摩尔–彭若斯广义逆；下列推导用满秩假设可直接左乘 \mathbf A^{\!\mathsf T}.）

更常见的 节点电压法：令 \mathbf v = \mathbf A^{\!\mathsf T}\mathbf V（ \mathbf V 为节点电位向量），再将 (1)(2) 组合可得

\boxed{\; \underbrace{\mathbf G}_{\mathbf G=\mathbf A\,\mathbf R^{-1}\mathbf A^{\!\mathsf T}}\,\mathbf V \;=\; \mathbf I_{\text{注入}} \;} \tag{4}

\mathbf G 称 节点导纳矩阵，对称且正定
若用网孔电流法，亦可得到
\mathbf Z\,\mathbf I_{\text{mesh}}=\mathbf V_{\text{mesh}},\qquad \mathbf Z \text{同样是对称正定}

3. 逻辑小结 = “证明”要点

步骤	关键条件	结果
(i) 单支路线性元件	v_k = i_k R_k	得到对角矩阵欧姆定律 (1)
(ii) KCL 写成 \mathbf A\,\mathbf i=\mathbf I_{\text{注入}}	线性约束①	提供电流耦合
(iii) KVL 写成 \mathbf A^{\!\mathsf T}\mathbf v=\mathbf 0	线性约束②	提供电压耦合
(iv) 将 (1) 代入 (ii)(iii)，消元 \mathbf i 或 \mathbf v	线性代数运算	得到节点（或网孔）矩阵方程 (4)

整个推导只用到 线性性 与 基尔霍夫定律，因此所有线性无源元件（R、L、C，在相量域内）均适用。
得到的矩阵 \mathbf G 或 \mathbf Z 就是“欧姆定律的矩阵推广”。
对称性和半正定/正定保障了解唯一性与数值稳定性。

小型两节点示例（验证）

电阻 R_1=50\,\Omega 连接节点 1–2，电阻 R_2=60\,\Omega 接地于节点 1，电阻 R_3=40\,\Omega 接地于节点 2，节点 1 注入电流 I_s=2\text{ A}（流入），节点 2 无外部注流。

构造 \mathbf A:

\mathbf A = \begin{bmatrix} +1 & +1 & 0\\ -1 & 0 & +1 \end{bmatrix}

\mathbf R=\operatorname{diag}(50,60,40)
\mathbf G=\mathbf A\,\mathbf R^{-1}\mathbf A^{\!\mathsf T}:
\mathbf G = \begin{bmatrix} \frac1{50}+\frac1{60} & -\frac1{50}\\ -\frac1{50} & \frac1{50}+\frac1{40} \end{bmatrix} = \begin{bmatrix} 0.03667 & -0.02\\ -0.02 & 0.045 \end{bmatrix}
结点方程：
\begin{bmatrix} 0.03667 & -0.02\\ -0.02 & 0.045 \end{bmatrix} \begin{bmatrix} V_1\\V_2 \end{bmatrix} = \begin{bmatrix} 2\\0 \end{bmatrix}

解得 V_1\approx78.5\text{ V},\; V_2\approx49.2\text{ V}，再回代可得各支路电流，与逐支路欧姆定律一致。

欧姆定律的矩阵形式并非“新定律”，而是“把一堆标量欧姆定律 + 基尔霍夫约束整理成线性代数表达”。
线性网络 → 线性映射 → 可以用矩阵描述；这就是欧姆定律推广的数学与物理根基。

单词表

#	English Word	中文释义
1	analysis	分析
2	amount	数量；量
3	around	围绕；大约
4	basic	基本的
5	battery	电池
6	best	最佳的
7	calculate	计算
8	circuit	电路
9	circulating	环流的
10	column	列；柱
11	combined	合并的；组合的
12	current	电流；当前的
13	currents	电流（复数）
14	DC (direct-current)	直流
15	equation	方程
16	equations	方程（复数）
17	first	第一；首先
18	follows	如下；跟随
19	gives	给出；提供
20	internal	内部的
21	joins	连接；结合
22	Kirchhoff’s	基尔霍夫的
23	label	标注；标签
24	laws	定律（复数）
25	list	列表；列出
26	loop	回路；循环
27	loops	回路（复数）
28	look-see	直观观察的
29	matrix	矩阵
30	mathematics	数学
31	method	方法
32	mesh	网孔
33	names	名称（复数）
34	next	下一步；下一个
35	nodal	节点的
36	number/th	第…（如 Nth）
37	probably	可能；大概
38	procedure	步骤；流程
39	reduces/reducing	减少；降低
40	resistance	电阻
41	R-inverse (R-1)	R 的逆矩阵
42	same	相同的
43	sources	电源；来源（复数）
44	states	说明；陈述
45	summary	总结
46	theory	理论
47	total	总计的
48	tutorial	教程
49	value	值；数值
50	vector	向量
51	voltage	电压
52	voltages	电压（复数）
53	write	写；书写

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。

Menu

Share

5.网孔电流分析

网孔电流分析

网孔电流分析

教程总结

附录

网孔电流分析逐步详解示例

1 电路描述与环流标注

2 写出 \mathbf V 列矩阵

3 构造电阻矩阵 \mathbf R

4 列矩阵方程并求解

5 求支路电流（公共 5 Ω 电阻）

矩阵形式的欧姆定律

为什么欧姆定律能够“升级”为矩阵形式？

1. 逐支路欧姆定律 ➜ 逐节点/逐网孔矩阵

1.1 单支路（标量）

1.2 收集成向量

2. 加入基尔霍夫定律：

2.1 KCL（节点电流定律）

2.2 KVL（回路电压定律）

2.3 联立 (1)(2)(3) 消元

3. 逻辑小结 = “证明”要点

小型两节点示例（验证）

单词表

声明

Comment

软件工程中的熵增定律

TOP命令详解

Postgresql数据库调优

正序负序零序详解

Linux的守护进程

虚拟内存辅助缓冲管理

书籍，文档，有趣的网站

Postgresql MVCC -1 隔离级别

Postgresql数据库维护须知

Simple Operation类型数据存储系统中可扩展性能的 10 条规则