基尔霍夫电路定律
基尔霍夫电路定律允许我们通过定义一系列关于电路中电压和电流的基本网络定律与定理来求解复杂电路问题。
利用基尔霍夫的电路定律中关于结点规则(Junction Rule)和闭合回路规则(Closed Loop Rule),只要已知电路中各个元件的数值,我们就可以计算并求出任意闭合电路中的电流和电压。
我们在电阻教程中已经看到,当两个或多个电阻以串联、并联或两者的组合方式连接时,可以求出一个等效电阻 R_T,并且这些电路遵循欧姆定律。
然而,对于桥式电路或 T 型网络等复杂电路,有时无法仅凭欧姆定律来求出电路中流动的电压或电流。对于此类计算,我们需要一些能够建立电路方程的规则,此时就可以使用基尔霍夫电路定律。
1845 年,德国物理学家古斯塔夫·基尔霍夫提出了一组处理电路中电流与能量守恒的定律。这两条定律通常称为基尔霍夫电路定律:其中一条处理流经电路结点的电流,称为基尔霍夫电流定律(Kirchhoff’s Current Law,KCL);另一条处理闭合回路中的电压分布,称为基尔霍夫电压定律(Kirchhoff’s Voltage Law,KVL)。
基尔霍夫第一定律——电流定律(KCL)
Kirchhoffs First Law – The Current Law, (KCL)
基尔霍夫电流定律(KCL)指出:流入某一结点或节点的总电流或电荷,恰好等于流出该结点的电流或电荷,因为电荷除了流出别无去处,且在结点内部不会丢失。
换句话说,所有流入和流出结点的电流代数和必须等于零:
基尔霍夫提出的这一思想通常称为电荷守恒Conservation of Charge。
基尔霍夫电流定律
Kirchhoffs Current Law
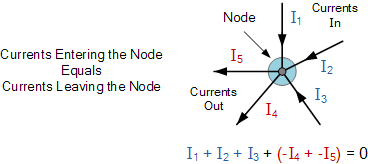
在此,流入该节点的三条电流 I_1、I_2、I_3 都为正值,而流出该节点的两条电流 I_4 和 I_5 则为负值。因此,我们也可以将方程改写为:
在电路中,“节点”(Node)通常指两条或多条载流路径或元件(如电缆、器件)相互连接或汇聚的地方。要使电流流入或流出某一节点,必须存在一个闭合的电路回路。在分析并联电路时,我们可以应用基尔霍夫电流定律。
基尔霍夫第二定律——电压定律(KVL)
Kirchhoffs Second Law – The Voltage Law, (KVL)
基尔霍夫电压定律(KVL)指出:在任何由电压源驱动的闭合回路中,环路上所有电压升降的代数和等于零。 换句话说,回路中所有电压源与电压降的代数和必须相等,因此它们的代数和为零。基尔霍夫提出这一思想即为能量守恒原理。
基尔霍夫电压定律
Kirchhoffs Voltage Law
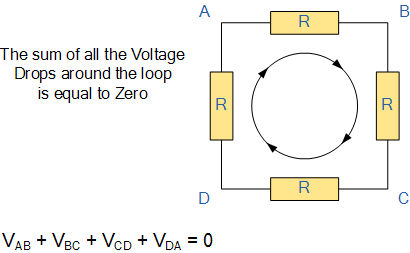
从回路的任意一点开始,沿同一方向(顺时针或逆时针均可)依次记录所有电压升降的正负方向,最后回到起始点时,所有电压代数和必为零。如果改变方向,最终电压和将不再为零。在分析串联电路时,我们可以应用基尔霍夫电压定律。
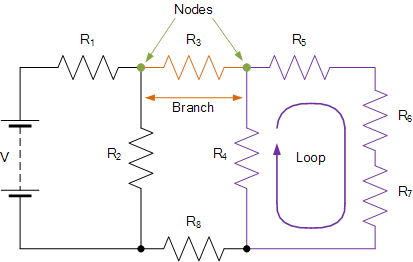
在使用基尔霍夫电路定律分析直流或交流电路时,常用以下术语来描述电路的各个部分:节点(node)、路径(path)、分支(branch)、回路(loop)和网孔(mesh)。这些术语在电路分析中频繁出现,理解它们非常重要。
常见直流电路理论术语
电路(Circuit) 电流流过的闭合导电路径。
路径(Path) 连接元件或电源的单一线路。
节点(Node) 两个或多个电路元件相连或汇聚的连接点,用一个实心点表示。
分支(Branch) 连接两个节点之间的一条或多条元件(如电阻或电源)。
回路(Loop) 电路中不重复经过任何元件或节点的简单闭合路径。
网孔(Mesh) 不包含其他回路的单一闭合串联路径,网孔内部没有更小的回路。
注:
串联:若所有元件中流过的电流值相同,则称这些元件串联连接。
并联:若所有元件两端施加的电压相同,则称这些元件并联连接。
典型的直流电路
A Typical DC Circuit
基尔霍夫定律例题1
求流过 40 Ω 电阻 R₃ 的电流。
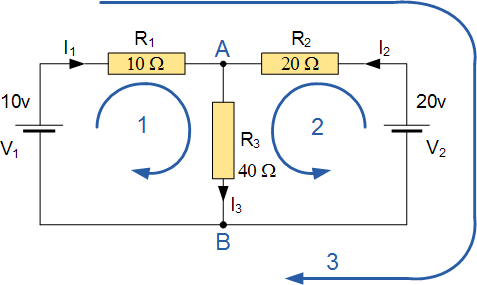
该电路共有 3 条支路、2 个节点(A 和 B)以及 2 个独立回路。
应用基尔霍夫电流定律 (KCL),方程为:
在节点 A:
I_1 + I_2 = I_3在节点 B:
I_3 = I_1 + I_2
应用基尔霍夫电压定律 (KVL),方程为:
回路 1:
10 = R_1 I_1 + R_3 I_3 = 10\,I_1 + 40\,I_3回路 2:
20 = R_2 I_2 + R_3 I_3 = 20\,I_2 + 40\,I_3回路 3:
10 - 20 = 10\,I_1 - 20\,I_2
由于 I_3 = I_1 + I_2,可将前两条方程改写为:
由此得到两个关于 I_1 和 I_2 的二元一次方程,通过减法消元可解得:
因为
所以流经电阻 R_3=40\ \Omega 的电流为
对应的电压降为
其中 I_1 为负值表示初始假定的电流方向与实际相反,但计算结果依然有效。实际上,20 V 电池正在给 10 V 电池充电。
此题可以有其他解决方法,参考附录中的例题1的更优解法
基尔霍夫电路定律的应用
这两条定律使得电路中的电流与电压得以求解,即对电路进行“分析”。使用基尔霍夫电路定律的基本步骤如下:
假设所有电压与电阻均已知(若未知,则标注为 V_1, V_2, \dots,R_1, R_2, \dots)。
给每条支路或网孔假设一个电流方向(顺时针或逆时针)。
在每条支路上标注支路电流( I_1, I_2, I_3 等)。
写出每个节点的基尔霍夫第一定律(KCL)方程。
写出电路中每个独立回路的基尔霍夫第二定律(KVL)方程。
根据需要建立线性方程组,求解未知电流。
除了使用基尔霍夫电路定律计算线性电路中各处的电压与电流外,我们还可以通过回路分析(Loop Analysis)来直接求取每个独立回路的电流,这样仅凭基尔霍夫定律就能减少计算量。在下一节直流电路教程中,我们将介绍网孔电流法(Mesh Current Analysis)来实现这一点。
附录
例题1的更优解法
除了列多条 KCL/KVL 方程再消元外,这道题用结点电压法(Nodal Analysis) 或 戴维南/诺顿等效 都能更快地一步到位。
方法一:结点电压法
令下端节点 B 为参考地(V_B=0),令节点 A 电压为 V_A。
对节点 A 写 KCL:三支路电流代数和为零
\frac{V_A - 10}{10} \;+\;\frac{V_A - 20}{20}\;+\;\frac{V_A - 0}{40}\;=\;0.整理:
\frac{V_A -10}{10}+\frac{V_A -20}{20}+\frac{V_A}{40} =0 \; \\ \longrightarrow\; 4(V_A-10)+2(V_A-20)+(V_A)=0 \; \\ \longrightarrow\; 7V_A=80 \; \longrightarrow\; V_A=\frac{80}{7}\approx11.43\ \text{V}.中央电阻 R_3=40\:\Omega 上电流:
I_3=\frac{V_A-0}{40}=\frac{80/7}{40}\approx0.286\ \text{A}.
整个过程只需解一个一元一次方程,非常简洁。
方法二:诺顿等效+电流分配
左支路等效成诺顿源:
I_{N1}=\frac{10\ \text{V}}{10\:\Omega}=1\ \text{A},\quad R_{N1}=10\:\Omega.右支路等效成诺顿源:
I_{N2}=\frac{20\ \text{V}}{20\:\Omega}=1\ \text{A},\quad R_{N2}=20\:\Omega.将两诺顿源并联,再并联上 R_3=40\:\Omega。并联等效电阻
R_\mathrm{eq}=\bigl(\tfrac1{10}+\tfrac1{20}+\tfrac1{40}\bigr)^{-1}= \frac{1}{0.175}=5.714\:\Omega.总电流来源于两个诺顿电流之和 I_{N1}+I_{N2}=2\:\text{A},在三支路中分配:
I_3 = (2\:\mathrm{A})\times\frac{1/40}{1/10+1/20+1/40} =2\;\frac{0.025}{0.175}\approx0.286\:\mathrm{A}.
同样一步即可得到 I_3。
以上两种方法都比列写三条 KVL、两条 KCL 再消元要简洁许多,推荐使用结点电压法!
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

