电容器简介

Introduction to Capacitors

电容器是一种简单的无源器件，当连接到电压源时，能够在其极板上储存电荷。

在本电容器入门教程中，我们将看到，电容器是一种无源电子元件，由两个或多个导电材料组成，这些导电材料彼此分离，中间由绝缘材料隔开。电容器具有以电荷形式储存能量的能力，从而在其极板之间产生电位差（静电压），类似于一个小型可充电电池。

市面上有各种各样的电容器，从在谐振电路中使用的微小电容珠，到用于功率因数校正的大型电容器，但它们的功能都是相同的——储存电荷。

在最基本的形式中，电容器由两块或多块并列的导电（金属）极板组成，这些极板既不相互连接也不接触，而是通过空气或某种优良的绝缘材料电气隔开。该绝缘材料可以是蜡纸、云母、陶瓷、塑料，或者电解电容中使用的某种液体凝胶。这个位于极板之间的绝缘层通常称为介电质（Dielectric）。

由于该绝缘层，直流电流无法流过电容器，因为它将电流阻断，而以电荷的形式在极板之间产生电压。

电容器的导电金属极板可以是方形、圆形或矩形，也可以是圆柱形或球形；平行板电容器的形状、尺寸和结构取决于其应用和额定电压。

​

A Typical Capacitor

​

在直流（DC）电路中，电容器会充电至其电源电压，但会阻止电流通过电容器本身，因为电容器的介电质是不导电的、基本上是绝缘体。然而，当电容器连接到交流（AC）电路时，电流似乎可以毫无阻力地“通过”电容器。

电荷有两种形式：正电荷（质子）和负电荷（电子）。当在电容器两端施加直流电压时，正（+ve）电荷会迅速在一极板上累积，而对应且相反的负（−ve）电荷则累积在另一极板上。每有一个正（+ve）电荷到达一极板，便会有一个相同符号的电荷从负（−ve）极板离开。

此时，极板保持电中性，并在两极板间建立由此电荷引起的电位差。一旦电容器达到稳态，由于介电质的绝缘特性，电流无法流经电容器本身或环路。

电子流向极板的过程称为电容器的充电电流Charging Current，该电流持续流动，直到两极板（以及电容器）上的电压等于施加电压 V_c。此时，电容器被称为完全充电fully charged状态。

当极板完全放电（初始状态）时，该充电电流的强度或速率达到最大值；随着极板充电至与电源电压相等的电位差，电流逐渐减小至零。

电容器两极板上存在的电位差取决于电源电压所做的功在极板上沉积的电荷量，以及电容器的电容量大小，如下所示。

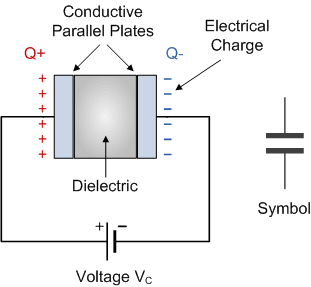
平行板电容器是电容器最简单的形式。它可由两块相互平行且保持一定距离的金属板或金属化箔板构成，其电容值（单位：法拉 F）由导电极板的表面积和它们之间的距离决定。改变上述任意两项参数都会改变其电容值，这也构成了可变电容器工作的基础。

此外，由于电容器以电荷形式在极板上储存电子的能量，极板面积越大和／或极板间距越小，在相同电压下电容器所能储存的电荷就越多。换言之，极板越大、距离越小，电容越大。

通过对电容器施加电压并测量极板上的电荷，将电荷 Q 与电压 V 的比值取出即能得到电容值，即

该公式也可变形为熟悉的电荷量公式

尽管常说电荷储存在电容器的极板上，但更准确地说，电荷所蕴含的能量是储存在两极板之间的静电场中的。当电流注入电容器时，电容器充电，使静电场随在极板之间储存的能量增多而增强。

同样地，当电流从电容器流出使其放电时，两极板间的电位差减小，随着能量的释放，静电场也随之减弱。

电容器以静电场形式在极板上储存电荷并抵抗跨端电压变化的特性称为电容Capacitance。不仅如此，电容也是电容器抵抗其两端电压变化能力的体现。

电容器的电容

The Capacitance of a Capacitor

电容是电容器的一种电学特性，用于衡量电容器向其两极板储存电荷的能力。电容的单位是法拉（Farad，缩写为 F），以英国物理学家迈克尔·法拉第（Michael Faraday）命名。

电容的定义：当在两极板上以一伏（1 V）电压存储一库仑（1 C）电荷时，电容器的电容即为一法拉。注意，电容 C 始终为正值，不存在负单位。然而，法拉作为计量单位较大，通常会使用其子倍单位，例如微法拉、纳法拉和皮法拉等。

电容的标准单位

根据上述换算关系，可构建下表，以便在皮法拉（pF）、纳法拉（nF）、微法拉（μF）和法拉（F）之间互相转换：

平行板电容器的电容与两个极板中面积较小的那一块的面积 A（单位： \mathrm{m}^2）成正比，与这两块导电极板之间的距离（即介电层厚度）d（单位：\mathrm{m}）成反比。

平行板电容器的通用电容公式为：

其中 \varepsilon 表示所用介电材料的绝对介电常数。介电常数 \varepsilon_0，也称“真空介电常数”，其值为

为简化计算，这一真空介电常数 \varepsilon_0 也可写作

并换算为以皮法拉每米（pF/m）为单位的常数，数值约为 8.85。但需注意，此时计算得到的电容值将是皮法拉而非法拉。

在实际中，电容器的极板之间通常隔有某种绝缘材料或凝胶，而非完全真空。在计算电容时，可将空气（尤其是干燥空气）的介电常数视同于真空，因为两者数值非常接近。

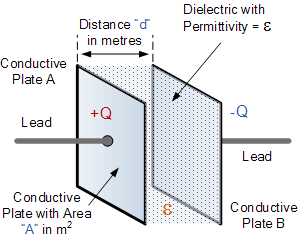
电容器入门示例1

一个电容器由两块尺寸为 30 cm × 50 cm 的导电金属极板构成，极板之间的间距为 6 mm，且仅以干燥空气作为介电材料。请计算该电容器的电容。

使用：

其中：

由此，由两块空气间隔的极板组成的电容器，其电容计算得 0.221\ \mathrm{nF}\quad\text{即}\quad221\ \mathrm{pF}.

电容器简介 — 介电质

Introduction to Capacitors – The Dielectric

除了导电极板的整体尺寸及其彼此之间的距离（即极板间介电层厚度）之外，影响电容器总电容的另一因素是所用介电材料的类型，亦即介电常数（Permittivity， \varepsilon）。

电容器的导电极板通常由金属箔或金属膜制成，以便电子和电荷在其中流动；而介电材料始终为绝缘体。不同的绝缘材料在阻挡或允许电荷移动方面具有不同能力。

常见的介电材料可由多种绝缘材料或它们的组合制成，最常用的类型包括：空气、纸张、聚酯（Polyester）、聚丙烯（Polypropylene）、聚酯薄膜（Mylar）、陶瓷、玻璃、油，以及其他各种材料。

介电材料（绝缘体）相对于空气能增加电容器电容的倍数称为介电常数 k。介电常数越高，材料的绝缘性能越好。由于介电常数是相对于自由空间而言的，因此它是无量纲的。

实际上，两极板之间介电材料的“复介电常数” \varepsilon 等于真空介电常数 \varepsilon_0 与该材料相对介电常数 \varepsilon_r 的乘积，即

Complex Permittivity

换句话说，当我们以真空介电常数 \varepsilon_0 为基准，并将其取值为 1 时，一旦真空被其他类型的绝缘材料所替代，该材料的介电常数就会相对于真空的基准介电常数产生一个倍增因子，称为“相对介电常数” \varepsilon_r。因此，复介电常数 \varepsilon 的数值始终等于相对介电常数 \varepsilon_r。

常见材料的介电常数（\varepsilon）或介电常数典型取值如下：

• 纯真空：1.0000

• 空气：1.0006

• 纸张：2.5–3.5

• 玻璃：3–10

• 云母：5–7

• 木材：3–8

• 金属氧化物粉末：6–20

由此可得电容器电容的最终公式为：

一种在保持体积小的同时增加电容器总电容的方法，是在单个电容器内部“交错”更多极板。与仅有一对平行极板不同，电容器可以将多块独立极板相互连接，从而增大极板的表面积 A。

对于如上所示的标准平行板电容器，它有两块极板，标记为 A 和 B。因此极板数为 n=2，其中 “n” 表示极板的总数。

那么，上述针对单一平行板电容器的公式实际上应当写为：

然而，电容器虽然有两块平行极板，但每块极板只有一侧与中间的介电质接触，另一侧则构成电容器的外部。如果将两块极板的两半拼接在一起，就等效于只有“一个”完整的极板与介电质接触。

对于单一平行板电容器，

因此

这与之前的标准公式完全一致。

现在，假设我们有一个由 9 块交错极板组成的电容器，则

多极板电容器

Multi-plate Capacitor

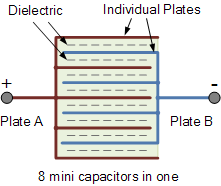
现在我们有五块极板连接到一个引线（A），四块极板连接到另一个引线（B）。连接到引线 B 的那四块极板的两面都与介电质接触，而连接到 A 的两个最外层极板只有一面与介电质接触。由此可知，每组极板的有效表面积均为八倍单个极板面积，因此其电容为：

现在我们有五块极板连接到一个引线（A），四块极板连接到另一个引线（B）。连接到引线 B 的四块极板的两面都与介电质接触，而连接到 A 的最外层两块极板只有一面与介电质接触。故如上所述，每组极板的有效表面积仅为八倍单块极板面积，其电容因此由下式给出：

现代电容器可根据其绝缘介电质的特性和属性分为：

• 低损耗、高稳定性，如云母、低介电常数陶瓷、聚苯乙烯。

• 中等损耗、中等稳定性，如纸介电容、塑料薄膜、高介电常数陶瓷。

• 极化电容，如电解电容、钽电容。

电容器简介 — 工作电压

Introduction to Capacitors – Voltage Rating

所有电容器都有一个最高工作电压额定值，选用电容器时必须考虑其两端所承受的电压。电容器所能承受而不损坏其介电材料的最大电压，通常在数据表中标注为 WV（工作电压，Working Voltage）或 WV DC（直流工作电压，DC Working Voltage）。

如果施加在电容器两端的电压过高，介电质就会击穿（称为电气击穿），并在极板间产生电弧，导致短路。电容器的工作电压取决于所用介电材料的类型及其厚度。

电容器的直流工作电压，仅指其所能承受的最大直流电压，而非 最大交流电压。比如，一只标称 100 V DC 的电容器，若承受 100 V 的交流电压，则无法安全工作，因为 100 V RMS 的交流电，其峰值电压超过 \sqrt{2}\times100\approx141,V。

因此，一只用于 100 V AC 工作的电容器，其工作电压应至少为 200 V。实际上，应选用工作电压（无论直流还是交流）至少比实际作用电压的有效值高出 50% 的电容器。

电容器简介 — 介电泄漏

Dielectric Leakage

另一个影响电容器性能的因素是介电泄漏。介电泄漏是指电容器内部介电材料中流过的不希望出现的泄漏电流。

通常假定介电质的电阻极高，是良好的绝缘体，能够阻断直流电流从一极板流向另一极板（理想电容器状态）。然而，如果介电质因过高电压或过高温度而受损，其介电泄漏电流将急剧增大，导致极板上的电荷迅速丢失，并使电容器过热，最终造成电容器提前失效。因此，切勿在超出电容器额定工作电压的电路中使用该电容器，否则可能过热甚至爆炸。

电容器简介 小结

我们在本教程中已经看到，电容器的作用是将电荷存储在其极板上。 电容器能在其极板上存储的电荷量称为其电容值，并且取决于三个主要因素。

• 表面积 —— 构成电容器的两块导电极板的表面积 A，面积越大，电容越大。

• 距离 —— 两极板之间的距离 d，距离越小，电容越大。

• 介电材料 —— 分隔两极板的材料称为“介电质”，其介电常数越高，电容越大。

我们还看到，电容器由互不接触的金属极板和称为介电质的材料隔开。电容器的介电质可以是空气，甚至是真空，但通常是非导电的绝缘材料，如蜡纸、玻璃、云母以及各种塑料等。 介电质具有以下优点：

• 介电常数是介电质的属性，不同材料的介电常数 k 值各不相同，可使电容按该倍数增加。

• 介电质在两极板之间提供机械支撑，使极板可以更靠近而不接触。

• 介电质的介电常数提高了电容值。

• 与空气相比，介电质提高了最大工作电压。

电容器可用于多种应用和电路，例如在阻断直流电流的同时传递音频信号、脉冲、交流电或其他时变波形。这种阻断直流电流的能力使电容器可用于平滑电源输出电压，去除信号中的不必要尖峰，以防止损坏或误触发半导体或数字元件。电容器还可用于调整音频电路的频率响应，或将相互独立的放大器级耦合起来，同时隔离直流电流的传输。

当电容器用于直流电源时，其阻抗为无限大（开路）；在极高频率下，其阻抗为零（短路）。所有电容器都有最大直流工作电压（WVDC）额定值，因此建议选择额定电压至少比实际电压高出 50% 的电容器。

我们在本电容器入门教程中已经看到，各种电容器样式和类型繁多，各具独特的优点、缺点和特性。要涵盖所有类型会使本章节篇幅过大，因此在下一节电容器教程中，我将仅限于介绍最常用的几种类型。

附录

为什么介电常数使用复数

在直流（DC）条件下，我们只需用实数的介电常数来描述介质对电场能量的储存；但在交流（AC）或高频应用中，介质极化并不是完全同步、电荷的累积也伴随着能量损耗（例如介质吸收、分子摩擦等），这时就需要用复数形式来同时描述“能量存储”与“能量损耗”的两种行为。

具体地，我们把介电常数写成

其中

• \varepsilon′（实部）表示介质对电场能量的储存能力；

• \varepsilon″（虚部）表示介质损耗所对应的能量耗散；

• 负号和虚数单位 j 用来体现电场与电位移场之间的相位滞后。

另外，一个常用的指标是损耗正切（loss tangent）：

它量化了在一个交流周期内，有多少能量被损耗掉。

因此，当我们在求解交流电或射频条件下的电容器特性时，就必须采用复数介电常数，才能准确反映介质既能“储能”又会“耗能”的双重特性。

电力电容器解剖图

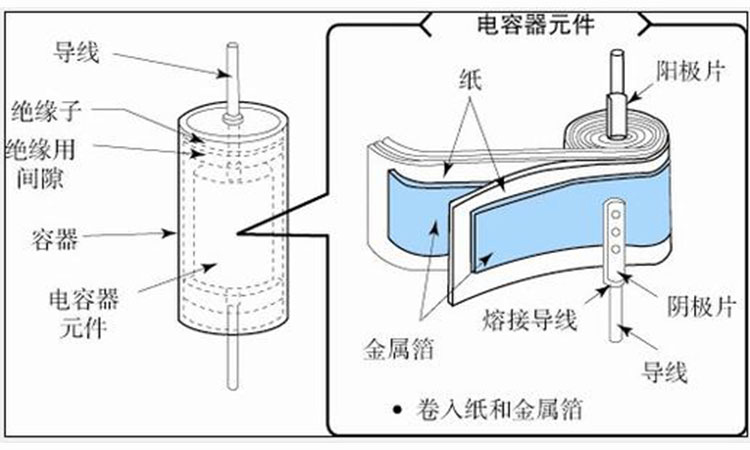
典型的电力补偿电容器由多个铝箔与复合薄膜绝缘材料卷制而成，内部单元通过熔丝串并联以提供故障保护，该组件整体浸渍于绝缘油或干燥空气中，并装入密封金属外壳或瓷套管内。

电容元件的核心结构是一层层金属箔与介电纸或薄膜交替卷制，卷心两端通过焊接导线与引线连接，形成高压耐压单元。

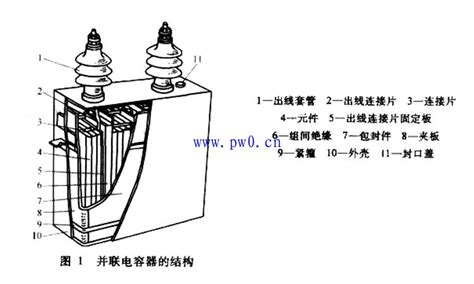
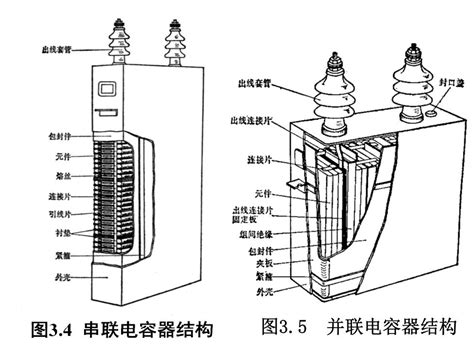
在高压串联补偿装置中，多个电容器单元串接以补偿线路感抗并抑制谐振，其外壳通常带有瓷套管和压力释放装置，如下图所示。

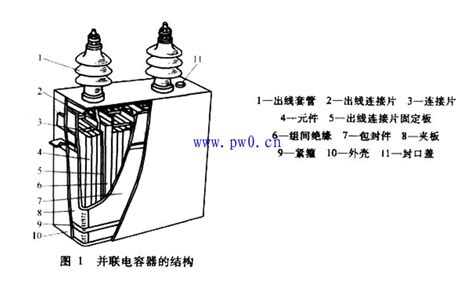
在低压或集中式无功补偿中，电容器单元并联连接到母线上，每相可配置多个并列单元，以根据负荷动态投切无功功率，如下图所示。

主要部件包括：

• 出线套管：用于高压接线穿引与绝缘隔离；

• 连接片：将内部卷制元件电气连接至引线；

• 卷制元件：铝箔与介电薄膜交替卷制的电容单元；

• 绝缘件：介电油或固态绝缘纸/薄膜；

• 固定板与外壳：提供机械支撑、散热及过压保护。

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。