组合串并联电路
Combination Series and Parallel Circuits
组合电路在同一电气回路中结合了串联和并联路径的电气特性。
串并联电路的组合
Combining Series and Parallel Circuits
我们之前已经看到,直流串联电路中流经电路的电流相等,直流并联电路中各支路电压相等。但是,当同时存在串联和并联的组合电路时,会发生什么?如何求解这些串并联组合电路,以确定各元件的电流和电压降呢?
串并联组合电路,顾名思义,是在同一电路中跨接于单一电源的串联和并联电路的组合。从之前的教程中我们知道,电压分配适用于串联元件,电流分配适用于并联元件。
直流串并联电路有时会以复杂电路的形式出现,由多个元件组成,以便从单一电源获得不同的电压和电流值。但通过将串联和并联电路组合在一起,我们可以分别求出串联部分和并联部分的等效值。
因此,在分析组合电路时,我们可以针对串联电路和并联电路分别使用不同的电路分析定律,从而在任意两点(或端子)之间得到一个更简单的等效电路,使我们能够求解电路中的未知电压、电流和电阻值。
但首先,让我们回顾一下直流串联电路和直流并联电路的特性。
直流串联电路
DC Series Circuit
串联电路的等效或总电阻 R_T 等于各个电阻之和。由于电流只能沿单一路径流动,电源 V_S 提供的总电流 I_T 因此在每个串联电阻上具有相同的数值,如图所示。
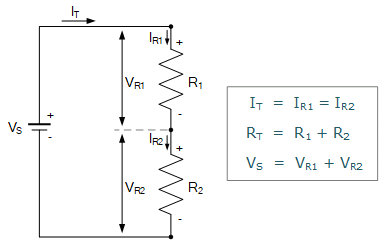
请注意,对于一串纯电阻组成的“串联回路”,各电阻上的电压降之和等于电源电压 V_S。因此,串联电路实现了电压分配(电压分压)。
直流并联电路
DC Parallel Circuit 并联电路是在同一电压源两端连接两个或多个元件。也就是说,电源电压 V_S 同时加在所有电路元件上。每一条并联支路都称为一个“支路”,如图所示,各支路将各自分担不同的电流。
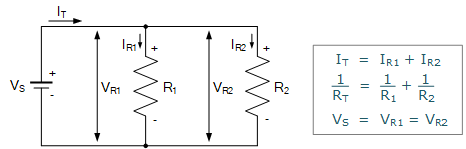
请注意,对于一串纯电阻组成的“串联回路”,每个电阻上的电压降之和等于电源电压 V_S。因此,串联电路实现了电压分配。
并联电路各支路电流之和等于电路中的总电流 I_T。每个支路的电阻值可用于将总电流按比例分配到各支路电流中。因此,并联电路实现了电流分配。
在回顾了串联电路和并联电路的结构、规律和特性后,我们现在可以将注意力转向串并联组合电路,以及如何求解此类串并联组合电路。
串并联组合电路
Combination Series and Parallel Circuits
串并联电路由串联电路和并联电路组合而成。组合方式的可能性是无穷的,因此任何两个电路都不会完全相同,因此必须针对具体电路单独分析和求解。
任何串联和并联电路的组合都可以通过简化来求解,即反复将任一串联或并联的元件组合替换为其等效电路。例如,将若干串联或并联的电阻替换为一根具有相同电路影响的等效电阻。
下面我们从以下这个串并联组合电路开始分析。
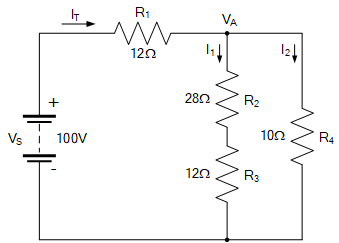
希望我们可以看到,上图电路中的电阻 R_2 和 R_3 是串联连接的。因此,串联电阻 R_S(R-series)等于:
将两个串联电阻 R_2 和 R_3 合并为一个等效电阻 R_S,其数值为 40\,\Omega。此时每条支路中仅剩一个电阻,我们可以将电路重新绘制如下:
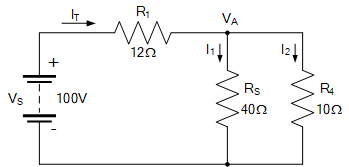
好的,现在我们应该可以看到电阻 R_S 和 R_4 是并联连接的。由于这是一个不同阻值的简单并联电路,我们可以使用倒数法则来求出两条并联支路的等效电阻 R_{\mathrm{EQ}},如下所示:
因此,将两个并联支路电阻 R_S 和 R_4 合并为一个等效电阻 R_{\mathrm{EQ}}=8\,\Omega。所得的等效电路现在大致如下:
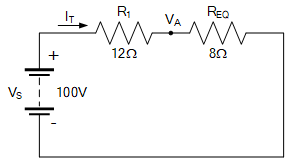
我们可以看到,剩余的两个电阻 R_1 和 R_{\mathrm{EQ}} 是串联连接的。因此,它们的总电阻 R_T 为:
因此,可以用一个等效电阻 20\,\Omega 来替换原电路中串并联组合的四个电阻。
接着,使用欧姆定律,电源提供的总电流 I_T 为:
由此可知,组合串并联电路中的电流为 5\,\mathrm{A}。
我们还可以进一步使用欧姆定律求出各支路电流 I_1、I_2 以及各电阻上的电压降。
首先,电阻 R_1 上的电压降和节点 A 的电压:
由于节点 A 的电压也是并联组合 (R_2 + R_3)\parallel R_4 上的电压,因此支路电流 I_2 为:
又因总电流等于两支路电流之和,即 I_T = I_1 + I_2,可得:
在电流 I_1=1\,\mathrm{A} 流经串联电阻 R_2 和 R_3 时,它们各自的电压降为:
检验节点 A 电压:
与前面计算结果一致。
以上即为在原串并联组合电路中标注了所有计算得出的电流和电压后的电路示意图。
最终串并联组合电路
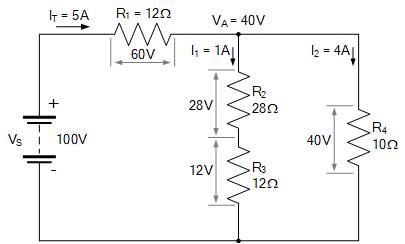
我们也可以(如果愿意)计算总功率消耗 P_T 或电路中各元件的耗散功率,因为电功率 P 等于:
然后,利用已知的 V_S = 100\,\mathrm{V}、I_T = 5\,\mathrm{A} 和 R_{\mathrm{EQ}} = 20\,\Omega,串并联组合电路的总功率消耗为:
因此各电阻的耗散功率为:
再次检验:
现在让我们尝试第二个示例,一个更复杂的电阻串并联组合电路。
串并联电路示例2
使用下列电路计算:电路的等效电阻 R_{\mathrm{EQ}}、从电源汲取的总电流 I_{T}、节点 A 的电压水平、各分支电流 I_{1} 和 I_{2},以及所有电阻上的电压降。
串并联组合电路
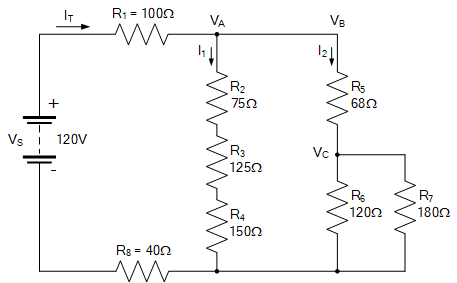
等效电阻 R_{\mathrm{EQ}}: 首先,电阻 R_{6} 与 R_{7} 并联,得到等效电阻 R_{10}:
\frac{1}{R_{10}} = \frac{1}{R_{6}} + \frac{1}{R_{7}} = \frac{1}{120} + \frac{1}{180} = 0.0125 \quad\Longrightarrow\quad R_{10} = \frac{1}{0.0125} = 72\ \Omega然后, R_{5} 与 R_{10} 串联,得到等效电阻 R_{11}:
R_{11} = R_{5} + R_{10} = 68 + 72 = 140\ \Omega再者,支路电阻 R_{2},R_{3},R_{4} 串联,得到等效电阻 R_{12}:
R_{12} = R_{2} + R_{3} + R_{4} = 75 + 125 + 150 = 350\ \Omega接着, R_{11} 与 R_{12} 并联,得到等效电阻 R_{13}:
\frac{1}{R_{13}} = \frac{1}{R_{11}} + \frac{1}{R_{12}} = \frac{1}{140} + \frac{1}{350} = 0.01 \quad\Longrightarrow\quad R_{13} = \frac{1}{0.01} = 100\ \Omega最后, R_{1}, R_{13}, R_{8} 串联,得到总等效电阻:
R_{\mathrm{EQ}} = R_{1} + R_{13} + R_{8} = 100 + 100 + 40 = 240\ \Omega总电流 I_{T}:
I_{T} = \frac{V_{S}}{R_{\mathrm{EQ}}} = \frac{120}{240} = 0.5\ \mathrm{A}节点 A 电压 V_{A}:
V_{A} = V_{S} - I_{T}R_{1} = 120 - (0.5 \times 100) = 70\ \mathrm{V}注意节点 B 与节点 A 相连,因此 V_{B}=V_{A}。
支路电流 I_{1}: 支路串联电阻总值为 R_{12}=350\ \Omega,其两端电压为节点 A 电压与节点 D 电压。节点 D 上的电压等于 I_{T}R_{8} = 0.5 \times 40 = 20\ \mathrm{V},故
I_{1} = \frac{V_{A} - V_{D}}{R_{12}} = \frac{70 - 20}{350} = 0.143\ \mathrm{A}支路电流 I_{2}: 支路串联电阻总值为 R_{11}=140\ \Omega,两端电压同样为 V_{A} 与 V_{D},故
I_{2} = \frac{V_{A} - V_{D}}{R_{11}} = \frac{70 - 20}{140} = 0.357\ \mathrm{A}各电阻电压降:
\begin{aligned} V_{R1} &= I_T R_1 = 0.5 \times 100 = 50\ \mathrm{V},\\ V_{R2} &= I_1 R_2 = 0.143 \times 75 = 10.7\ \mathrm{V},\\ V_{R3} &= I_1 R_3 = 0.143 \times 125 = 17.9\ \mathrm{V},\\ V_{R4} &= I_1 R_4 = 0.143 \times 150 = 21.4\ \mathrm{V},\\ V_{R5} &= I_2 R_5 = 0.357 \times 68 = 24.3\ \mathrm{V},\\ V_{R6} &= V_{R7} = V_C = V_A - V_{R5} = 70 - 24.3 = 45.7\ \mathrm{V},\\ V_{R8} &= I_T R_8 = 0.5 \times 40 = 20\ \mathrm{V}. \end{aligned}
如有需要,还可以计算总功率消耗:
以及各电阻的耗散功率。
组合串并联电路总结
我们已经看到,直流组合串并联电路不过是以各种方式组合的串联电路与并联电路的集合。串并联组合电路使得能够将串联电路的电压分配特性与并联电路的电流分配特性相结合。
将电阻按串联或并联方式组合,也可以将任何串联或并联连接的电阻化简为单一等效电阻 R_{\mathrm{EQ}},并将其置于同一电压源两端。
组合串并联电路的主要特性定义如下:
■ 电流流动:
– 在串联部分,电流在串联支路中的所有元件中相同。
– 在并联部分,总电流 I_T 等于分布在不同并联支路上的各电流之和。
■ 电压分配:
– 在串联部分,各元件上的电压降各不相同,从而实现电压分配,总电压等于各电压降之和。
– 在并联部分,各并联支路上的电压相同,各支路承受相同的电压等级。
■ 等效电阻:
– 在串联部分,总电阻等于串联支路中所有电阻之和,其值大于其中最大的单个电阻。
– 在并联部分,总电阻的倒数等于各支路电阻倒数之和,其值小于最小的单个电阻。
■ 功率分配: 可根据所知的两项,使用标准公式
– 在串联部分,功率耗散取决于电流;
– 在并联部分,功率耗散取决于电压。
简化组合串并联电路
理解和分析组合串并联电路通常需要将其拆分为更简单的串联或并联部分,以便计算总电阻、电压降和电流分布,因为将电路化简为更简单的形式后求解会更加容易。
确定串并联组合电路的等效电阻需要逻辑性的逐步分析,从而求出各元件上的电压降和电流。
第一步是识别纯串联和纯并联区段,然后通过逐一化简串联或并联组合,将电路拆分为更简单的部分。
继续化简串并联组合,直到得到整个电路的单一等效电阻 R_{\mathrm{EQ}}。一旦求得总电流 I_T,再逆向计算各元件的电压降、电流和功率耗散。
良好的验证做法是:
检查串联部分各元件的电压降之和是否等于总施加电压(电压分配检验);
检查并联部分各支路电流之和是否等于并联支路所吸收的总电流(电流分配检验)。
通过系统的“化简—求解—回代”方法,可以解决任何直流串并联组合电路的分析问题。
附录
单词表
声明
本文仅供学习,禁止用于任何的商业用途。

