直流并联电路
DC Parallel Circuit
并联电路是包含两个或多个电流分支的电路,但对每一个并联连接的元件而言,都具有相同的电压。
什么是直流并联电路
What Is a DC Parallel Circuit
直流并联电路(DC Parallel Circuit,或称“分支连接电路”)是将各个电子元件并联连接,使它们共享同一个电压源。直流并联电路与串联电路相对或互补。
并联电路的主要特征是它们仅有两个节点,每个元件和/或电源都连接在这两个节点之间。节点是电路中两个或更多电路元件相连的点,用作连接点。
由于直流并联电路中的所有元件仅共享两个节点,因此不存在其他连接或结点可用来产生额外的降压或形成分压网络。因此,并联电路中每个元件上的电压相同,无论该元件是电阻、电容还是电感,只要它们并联,所承受的电压大小都完全相同。
因为所有并联元件只共享两个节点,并且没有其他节点或路径让外部电流流出或进入电路,或让电压在任何点被分割,所以电源电流 I 会根据各分支的电阻或阻抗值进行分配。在并联电路中,只有一个共同的电压存在于所有元件上,但电流可以沿多条不同路径流动。每一条电流流动的并联路径通常称为“分支”。
直流并联电路示意图
DC Parallel Circuit Diagram
考虑下列直流并联电路示意图:四个电阻并联连接于一个 24 伏特电池电源的两端。节点 1、2、3 和 4 都连接到点 A;节点 5、6、7 和 8 都连接到点 B。因此,每个电阻都连接在同一对节点 A 和 B 之间,且它们共享相同的电池电压。
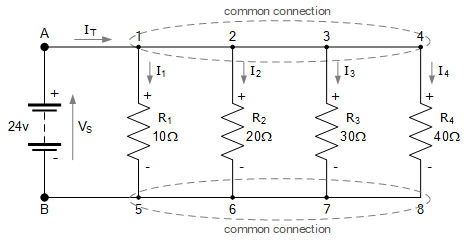
第一个电阻 R_1 上的电压等于电池电压 24 V,即节点 A 与节点 B 之间的电压。所以我们可以正确地表示为:
电流分配与欧姆定律
Current Division and Ohm’s Law
并联电路也可视作“电流分配器”,因为电源电流可在各分支间分流。电源电流的值等于各分支电流之和。根据欧姆定律:
流经并联电路电阻 R_1 的电流为
同理可得各分支电流:
代入数值:
并联电路中的电流
Current Flow in a Parallel Circuit

根据基尔霍夫电流定律(KCL),各分支电流之和等于电路总电流 I_T:
然后我们可以看到,源电流 I_T(数值为 5\,\mathrm{A})到达电路中的第一个节点(标记为“1”),随后在各并联支路之间分流。当电路的两个或更多分支在同一节点汇合时,电流会重新合流回电池。因此,总电流等于流经每个并联支路的电流之和。同时,我们也可以看到,各支路中的电流数值各不相同。
如果并联电路的各支路电阻值相同,则每个支路的电流也相同;反之,若各支路电阻值不同,则各支路电流也会不同。在并联电路中,由于每个电阻器两端的电压相同,较小的电阻(阻值较低)会有更大的电流流过,而较大的电阻(阻值较高)则电流较小。
因此,具有 “n” 条支路的并联电路将拥有 n 条不同的电流路径,并且根据欧姆定律可知:对于给定电压,电阻越大,电流越小。还要注意,如果任一并联路径发生断路(开路),电流仍会继续流经其他所有连通的并联路径,而总电源电流 I_T 则会相应减少等同于先前由该断路支路所承载的电流。
因此请记住:“分压器法则”(Voltage Divider Rule)基于串联电路,因为串联电路中电流处处相同;而“电流分配法则”(Current Divider Rule)基于并联电路,因为并联电路中电压处处相同。
总电阻或等效电阻
Total or Equivalent Resistance
我们已经看到,总电流 I_T 等于所有分支电流之和,并且通过应用欧姆定律可以计算并联电路的总等效电阻。但是,如果我们没有电压源 V_S 或者不知道总电流 I_T,那么如何计算并联电路的电阻呢?
在上述并联电路示例中, 24 \mathrm{V} 电池电源所“看到”的总或等效电阻 R_{\mathrm{EQ}} 等于所有单个电阻分支倒数之和的倒数。也就是说,先求出每个电阻值的倒数,然后将这些倒数相加,再用 1 除以相加所得的数值,即可得到并联电阻的等效电阻。
数学上,对于四个分支的并联电阻,关系可表示为:
然后,我们可以将上述并联电路的等效电阻计算为:
因此,并联组合的等效电阻 R_{\mathrm{EQ}} 计算为:
我们可以通过先前计算的电池供电电流 5\,\mathrm{A} 来验证该值。根据欧姆定律
可知电源所“看到”的总等效电阻为
与上述计算一致。
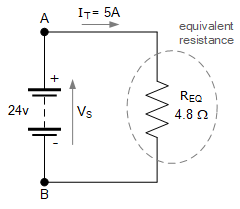
另外,并联电路的总等效电阻始终小于任何单个分支电阻。在本例中, 4.8\,\Omega远小于最小分支电阻 10\,\Omega。等效电路可表示如下:
并联等效电路
Equivalent Parallel Circuit
并联电路的电导
Conductance of a Parallel Circuit
在直流并联电路的计算中,使用大量倒数值既不直观,也容易混淆。然而,电阻的倒数称为电导(Conductance,记作 G)。
因此,如果电阻的阻值为 R,则其电导为 G = 1/R。我们可以用电导而非电阻来描述直流并联电路,这对并联电路更合理,也更易于计算。
根据欧姆定律,电导定义为电流比上电压:
并联电路的总电导等于各分支电导之和;并联路径越多,电路的整体电导越大。由于 G = 1/R,总电导可写为:
注意,电导的标准单位是“亥姆”(mho,即“ohm”倒拼),符号为 ℧;在国际单位制中,其单位为西门子(Siemens,符号 S),定义为每伏特的安培。
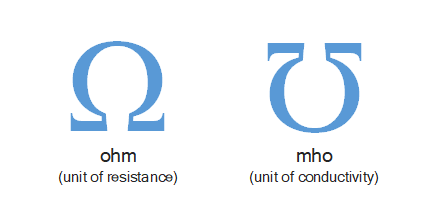
也就是说,当欧姆(Ω)是电阻的单位时,亥姆(mho)是电阻的倒数(Ω⁻¹)。另外,电阻可以用千欧(kΩ)或兆欧(MΩ)来表示,而电导的相应单位则是毫西(mS)或微西(μS)。例如: 10 kΩ = 100 μS。
因此,若电阻 R 以欧姆表示,电导 G 以西门子(S)表示,则每个电导 G 的数值都是对应电阻 R 的倒数:
对于上面简单并联电路示例,各分支的总电导 G_T 计算如下:
Total Circuit Conductance
然后:
与之前的计算结果相同,因为
由此可见,电导相加无需求倒数,也不需复杂运算。注意,并联电阻可互换位置,但等效电阻和总电导保持不变。
两个并联电阻的特殊情况 当仅有两个电阻并联且阻值不同,由于只有两条电流路径,可直接用“乘积除以和”法计算等效电阻,公式为:
该公式仅适用于两个元件并联,使计算更简便,无需先求倒数;若并联元件超过两个,则仍需使用倒数求和公式。
因此,对于下图所示的两电阻并联电路,我们可以计算总电阻 R_T:
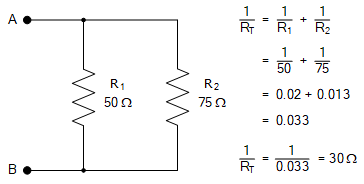
使用新的两个电阻的并联公式可得:
当 R_1 = R_2 时,网络的等效电阻恰好是任一电阻值的一半,即
同理,若三条或更多电阻值相同,则等效电阻为
其中 R 为每个电阻的阻值, n 为并联支路数。因此,任意数量相同电阻并联时的总电阻,等于单个电阻值除以并联分支数。
例如,若六个 100\,\Omega 电阻并联,则等效电阻为
但请注意,此方法仅适用于所有电阻值都相同的情况,否则必须使用倒数求和法(即 \displaystyle \frac{1}{R_{\rm EQ}}=\sum\frac{1}{R_i})。
并联电路教程总结
我们在此看到,直流并联电路(或称分流电路)是将两个或多个电路元件直接并联连接于两节点之间,从而在同一电压源上产生两条或多条电流通路。
并联电路的主要特性如下: ■ 电压一致性:并联电路中各分支元件两端的电压相同,因为它们都直接并联于同一电压源两端。 ■ 电流分配:由于存在两条或多条电流通路,电源提供的总电流等于流经每个并联分支的电流之和。各分支电流可因电阻不同而不同。 ■ 总电阻:并联电路的总电阻(等效电阻)小于电路中任何单一元件的最小电阻。总电阻的倒数等于各分支电阻倒数之和;增加并联分支可降低电路的总电阻。
我们还根据基尔霍夫电流定律(KCL)看到,各并联分支电流之和等于电源电流。由于电路中每个元件两端电压相同,可利用欧姆定律计算各分支电流。流经每个元件的电流与其电阻或阻抗(对有源元件)成反比。
由于电阻的倒数 1/R 称为电导(G),单位为西门子(S),在并联电路中直接使用电导而非电阻来计算各分支电流更为方便,可避免繁琐的倒数运算。
附录
单词表
声明
本文仅供学习,禁止用于任何的商业用途。

