
数据结构简介
为了更好的理解数据库中数据的存储,组织和操作,数据结构是绕不开的一个基础项目。
系统的理解数据结构,对于高效开发是非常有必要的。对于运维工作而言,学习数据结构可以让功力加深,尤其是对软件架构部分。
常用的数据结构包括 数组、链表、堆栈、队列、树和图
1. 什么是数据结构
按照wiki的说法,数据结构是一种数据组织,以及通常为有效访问数据而选择的存储格式。更准确的说,是一种代数结构
数据结构提供给函数或者操作集合具体的数据值。定义数据结构是为了更好的使用数据。
2. 数据结构分类
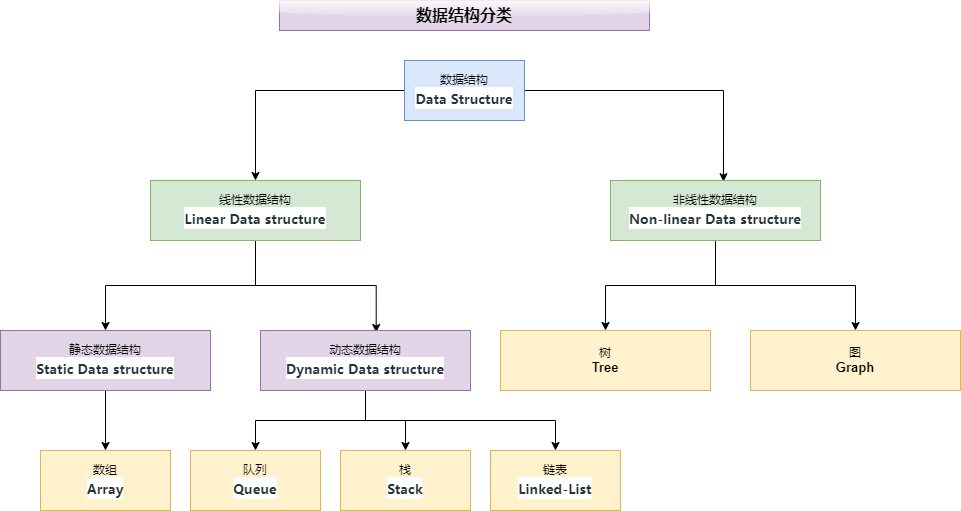
为了方便理解,我们将数据结构进行了分类
线性结构:数据元素按顺序或线性排列的数据结构,其中每个元素都附加到其上一个和下一个相邻元素,称为线性数据结构
静态数据结构:静态数据结构具有固定的内存大小。访问静态数据结构中的元素更容易
动态数据结构:在动态数据结构中,大小不固定。它可以在运行时期间随机更新。这在代码的内存(空间)复杂性方面可能被认为是高效的
非线性数据结构:数据元素不按顺序或线性放置的数据结构称为非线性数据结构。在非线性数据结构中,我们无法仅通过一次遍历就访问所有元素。非线性数据结构的例子有树和图。
注意,许多数据结构是复合型的,比如B+树就是一个平衡二叉树+链表实现的,这里的数据结构只是一个轮廓,是基础。
往往人们容易将数据类型和数据结构混肴,这里给出两者的不同之处
属性
数据类型
数据结构
定义
变量的形式,可以赋值。定义特定变量只会分配给定数据类型的值。
不同类型数据的集合。整个数据可以用一个对象表示,并在整个程序中使用。
持有值
只能持有值,但不能持有数据。因此,它是无数据的。
可以在单个对象中持有多种类型的数据。
实现
数据类型的实现称为抽象实现。
数据结构的实现称为具体实现。
时间复杂度
没有时间复杂度。
在数据结构对象中,时间复杂度起着重要作用。
内存
数据类型的值不存储,因为它只表示可以存储的数据类型。
数据结构中,数据及其值占据计算机主内存的空间。数据结构可以在一个对象中持有不同类型和种类的数据。
示例
int, float, double 等。
栈、队列、树等。
下面我们将对这几类主要的数据结构做一个简单介绍
2.1 数组
数组是一种线性数据结构。
它是存储在连续内存位置上的项目集合。其核心思想是将多种相同类型的项目集中存放在一个地方。这使得在相对较短的时间内处理大量数据成为可能。数组的第一个元素通过下标0进行索引。在数组中可以进行不同的操作,例如搜索、排序、插入、遍历、反转和删除。
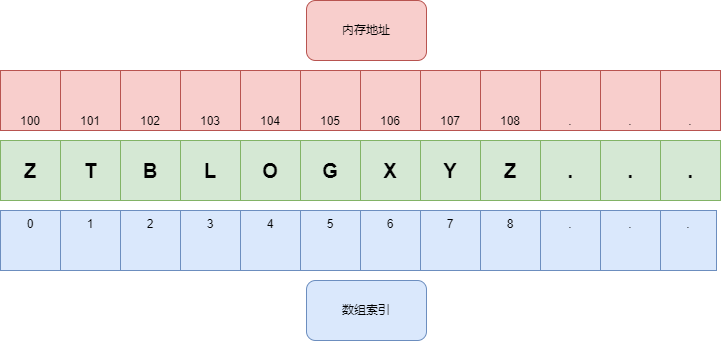
数组的特征
数组使用基于索引的数据结构,这有助于使用索引轻松识别数组中的每个元素。
如果用户想要存储相同数据类型的多个值,则可以有效地利用数组。
数组还可以通过将数据存储在二维数组中来处理复杂的数据结构。
数组还用于实现其他数据结构,如堆栈、队列、堆、哈希表等.
数组中的搜索过程可以非常容易地完成。
数组的操作
Initialization
初始化:可以在声明时或稍后使用赋值语句用值初始化数组。
Accessing elements
访问元素:可以通过索引来访问数组中的元素,索引从 0 开始,一直到数组大小减一。
这有点像每次排队做操前,教练会喊9527,通过这个编号索引,直接找到唐伯虎,而不用从头开始一个人一个人看。
Searching for elements
搜索元素:可以使用线性搜索或二分搜索算法在数组中搜索特定元素。
Sorting elements
对元素进行排序:可以使用冒泡排序、插入排序或快速排序等算法按升序或降序对数组中的元素进行排序。
Inserting elements
插入元素:可以将元素插入到数组的特定位置,但此操作可能非常耗时,因为它需要移动数组中的现有元素。
Deleting elements
删除元素:可以通过移动后面的元素来填补空白,从而从数组中删除元素。
Updating elements
更新元素:可以通过为特定索引分配新值来更新或修改数组中的元素。
Traversing elements
遍历元素:可以按顺序遍历数组中的元素,每个元素访问一次。
数组的作用
数组用于解决矩阵
matrix问题。数据库记录也是通过数组来实现的。比如pg中的tuple。
它有助于实现排序算法。
它还用于实现其他数据结构,如堆栈、队列、堆、哈希表等。
数组可以用于CPU调度。
数组在CPU调度中的应用主要体现在以下几个方面:
就绪队列:在操作系统中,调度程序需要维护一个就绪队列,存放所有已经准备好被CPU执行的进程。这个就绪队列可以使用数组来实现。每个数组元素可以存储一个进程控制块(PCB),其中包含进程的状态、优先级、CPU时间片等信息。
优先级队列:某些调度算法(如优先级调度)需要根据进程的优先级进行调度。可以使用多个数组来实现不同优先级的队列。每个优先级都有一个对应的数组,存放相应优先级的进程。调度程序通过扫描这些数组来选择优先级最高的进程进行调度。
循环队列(Round Robin 调度):在时间片轮转调度中,可以使用循环数组(环形缓冲区)来实现。进程按照顺序进入数组,当到达数组末尾时会回到数组的起始位置,从而实现循环调度。每个时间片结束后,调度程序会从数组中取出下一个进程进行调度。
多级反馈队列:这种调度算法使用多个数组,每个数组代表一个队列,存放不同优先级的进程。当进程在某个队列中用完了时间片但未完成时,会被移动到下一个优先级较低的队列的数组中。这种方式可以实现动态调整进程的优先级。
可以用作计算机中的查找表
lookup table。
假设我们需要频繁计算从0到255的平方,可以使用查找表预先存储这些结果:
# 预先计算平方值并存储在查找表中 lookup_table = [x**2 for x in range(256)] # 使用查找表快速查找平方值 def get_square(n): return lookup_table[n] # 示例 print(get_square(10)) # 输出 100
尽管它可能会增加内存使用,但在需要频繁计算或查找的场景中,查找表可以显著提高程序的效率。
数组可用于语音处理,其中每个语音信号都是一个数组。
计算机的屏幕也是通过数组来显示的。这里我们使用多维数组。
2.2 链表
链表是一种线性数据结构,其中元素不存储在连续的内存位置。链表中的元素使用指针链接,如下图所示:

链表的种类
Singly-linked list 单链表

Doubly linked list 双向链表

Circular linked list 循环链表

Doubly circular linked list 双向循环链表

链表的特点
链表使用额外的内存来存储链接。
在初始化链表时,不需要知道元素的大小。
链表用于实现栈、队列、图等。
链表的第一个节点称为头节点(Head)。
链表中最后一个节点的下一个指针总是指向NULL。
在链表中,插入和删除操作非常容易。
链表的每个节点包含一个指针/链接,指向下一个节点的地址。
链表可以随时轻松地缩小或增长。
链表的操作
链表是一种线性数据结构,其中每个节点包含一个值和对下一个节点的引用。以下是链表中常见的一些操作:
初始化:可以通过创建一个头节点并引用第一个节点来初始化链表。每个后续节点包含一个值和对下一个节点的引用。
插入元素:可以在链表的头部、尾部或特定位置插入元素。
删除元素:可以通过更新前一个节点的引用,使其指向下一个节点,从而有效地将当前节点从链表中移除。
查找元素:可以通过从头节点开始,沿着对下一个节点的引用,直到找到所需元素为止,来在链表中查找特定元素。
更新元素:可以通过修改特定节点的值来更新链表中的元素。
遍历元素:可以通过从头节点开始,沿着对下一个节点的引用,直到到达链表的末尾,来遍历链表中的元素。
反转链表:可以通过更新每个节点的引用,使其指向前一个节点而不是下一个节点,从而反转链表。
这些是链表中最常见的一些操作。具体的操作和算法可能会根据问题的要求和使用的编程语言而有所不同。
链表的应用
链表的不同应用如下:
链表用于实现堆栈、队列、图等。
链表用于对长整数执行算术运算。
它用于表示稀疏矩阵。
它用于文件的链接分配。
它有助于内存管理。
链表在内存管理中的应用主要体现在以下几个方面:
动态内存分配 链表能够高效地进行动态内存分配和释放。当需要为数据结构分配内存时,链表可以按需分配内存,并且当不再需要这些内存时,可以轻松地将其释放回内存池。这种按需分配和释放的机制有效地避免了内存浪费和内存碎片问题。
空闲内存块管理(自由链表) 在操作系统和内存管理系统中,链表常用于管理空闲内存块。所谓自由链表(free list),是指所有空闲内存块形成的链表。当内存块被释放时,会将其插入自由链表中;当需要分配内存时,从自由链表中找到合适的内存块进行分配。这种方法可以高效地管理和分配内存。
内存池管理 内存池(memory pool)是一种预先分配大块内存并将其划分为小块的方法,用于频繁的小内存分配场景。链表可以用于管理这些小块内存。内存池中的每个小块可以通过链表节点来表示,这样在需要分配或释放小块内存时,可以通过链表进行高效的操作。
分页内存管理 在分页内存管理中,链表可以用于管理页表。页表用于记录虚拟内存地址到物理内存地址的映射。每个页表条目可以通过链表节点来表示,这样可以方便地进行页表的增删改查操作。
堆管理 在堆管理中,链表常用于管理堆空间中的内存块。通过链表,可以有效地组织和管理堆中的已分配和未分配的内存块,确保内存的高效利用。
栈内存管理 链表也可以用于栈内存管理,尤其是当栈的大小不固定或需要频繁调整时。通过链表,可以实现一个动态的栈结构,使得栈的操作更加灵活和高效。
它用于表示多项式操作,其中每个多项式项表示链表中的一个节点。
链表用于显示图像容器。用户可以查看过去、当前和下一张图像。
它们用于存储访问过的页面历史记录。
它们用于执行撤销操作。
实现链表中的撤销操作通常需要借助一个辅助数据结构来记录操作历史,以便在需要撤销时恢复到之前的状态。常见的辅助数据结构是栈(stack),因为栈遵循后进先出(LIFO)的原则,非常适合用于实现撤销操作。
下面是一个简单的例子,展示如何使用链表和栈来实现撤销操作:
首先定义链表节点类和链表类。
定义一个栈来记录每次对链表的操作。
实现插入、删除和撤销操作。
class Node: def __init__(self, data): self.data = data self.next = None class LinkedList: def __init__(self): self.head = None self.history = [] def insert(self, data): new_node = Node(data) new_node.next = self.head self.head = new_node self.history.append(('insert', new_node)) def delete(self): if self.head is None: return None deleted_node = self.head self.head = self.head.next self.history.append(('delete', deleted_node)) return deleted_node.data def undo(self): if not self.history: print("No operations to undo") return operation, node = self.history.pop() if operation == 'insert': self.head = self.head.next # Remove the recently inserted node elif operation == 'delete': node.next = self.head self.head = node # Reinsert the deleted node def display(self): current = self.head while current: print(current.data, end=" -> ") current = current.next print("None") # 示例用法 ll = LinkedList() ll.insert(10) ll.insert(20) ll.insert(30) print("链表状态:") ll.display() # 输出: 30 -> 20 -> 10 -> None ll.delete() print("删除一个节点后:") ll.display() # 输出: 20 -> 10 -> None ll.undo() print("撤销删除操作后:") ll.display() # 输出: 30 -> 20 -> 10 -> None ll.undo() print("撤销插入操作后:") ll.display() # 输出: 20 -> 10 -> None在这个示例中:
Node类用于表示链表中的节点。LinkedList类用于表示链表,并包含一个栈(history)来记录操作历史。insert方法用于在链表头部插入新节点,并将操作记录到栈中。delete方法用于删除链表头部的节点,并将操作记录到栈中。undo方法用于撤销上一次操作,根据栈顶记录的操作类型进行相应的撤销。display方法用于显示链表的当前状态。
链表用于软件开发中指示标签的正确语法。
链表用于显示社交媒体动态。
链表的实际应用
链表用于轮询调度(Round-Robin scheduling),以跟踪多人游戏中的轮次。
链表用于图像查看器。前一张和下一张图像是链接的,因此可以通过前一张和下一张按钮访问。
在音乐播放列表中,歌曲与前一首和后一首歌曲相链接。
所有的数据结构都可以通过数组或者链表或者两者的结合来实现,无非是一个取舍问题
数据占用的内存空间连续紧凑,而链表占用的内存空间离散,这将带来一个系统开销问题。
2.3 栈
栈是一种线性数据结构,它按照特定的顺序执行操作。这种顺序是后进先出(LIFO)。
数据的输入和取出只能从一端进行。
数据的输入和取出操作分别称为压栈(push)和弹栈(pop)操作。在栈中可以执行各种操作,例如使用递归反转栈、排序、删除栈的中间元素等。
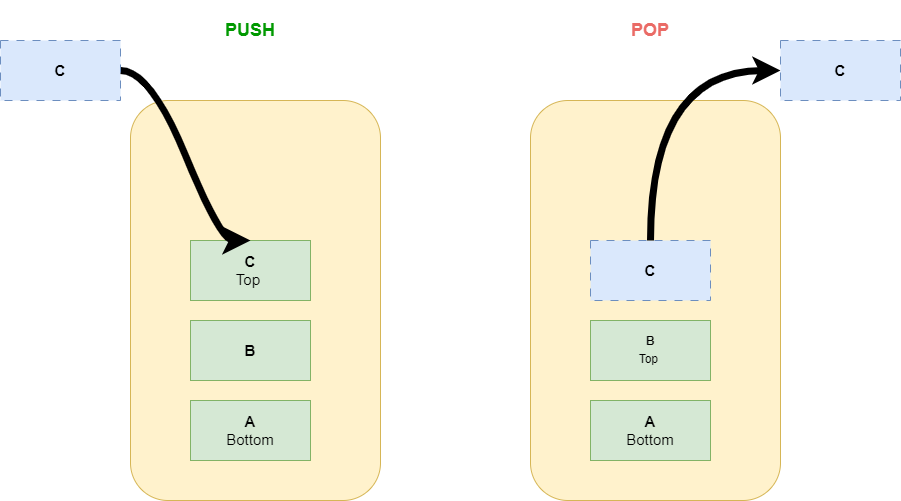
栈的特性
栈具有以下各种不同的特性:
栈被广泛应用于许多不同的算法中,如汉诺塔问题、树遍历、递归等。
栈可以通过数组或链表来实现。
它遵循后进先出(LIFO)操作,即先插入的元素最后弹出,反之亦然。
插入和删除操作都在栈的一端进行,即从栈顶操作。
在栈中,如果为栈分配的空间已满,仍然尝试添加更多元素,就会导致栈溢出
StackOverflow。
栈的应用
栈的不同应用如下:
栈数据结构用于算术表达式的求值和转换。
它用于括号匹配检查。
# 经典的算法问题 def is_balanced(expression): stack = [] for char in expression: if char in "({[": stack.append(char) elif char in ")}]": if not stack: return False top = stack.pop() if char == ')' and top != '(': return False elif char == '}' and top != '{': return False elif char == ']' and top != '[': return False return len(stack) == 0 expression = "{[()()]}" print(is_balanced(expression)) # 输出True 在反转字符串时,也使用了栈。
def reverse_string(s): stack = list(s) reversed_string = "" while stack: reversed_string += stack.pop() return reversed_string s = "Hello, World!" print(reverse_string(s)) # 输出"!dlroW ,olleH" # 除了栈,你可以更优雅的实现 def reverse_strings(s): return s[::-1]栈用于内存管理。
栈还用于处理函数调用。
栈用于将表达式从中缀转换为后缀。
栈用于在文字处理器中执行撤销和重做操作。
class TextEditor: def __init__(self): self.text = "" self.undo_stack = [] self.redo_stack = [] def write(self, text): self.undo_stack.append(self.text) self.text += text def undo(self): if self.undo_stack: self.redo_stack.append(self.text) self.text = self.undo_stack.pop() def redo(self): if self.redo_stack: self.undo_stack.append(self.text) self.text = self.redo_stack.pop() def __str__(self): return self.text editor = TextEditor() editor.write("Hello") editor.write(", World") print(editor) # 输出"Hello, World" editor.undo() print(editor) # 输出"Hello" editor.redo() print(editor) # 输出"Hello, World"栈用于像JVM这样的虚拟机中。
栈用于媒体播放器中,有助于播放下一首和上一首歌曲。
栈用于递归操作。
def fibonacci(n): if n <= 1: return n else: return fibonacci(n-1) + fibonacci(n-2) print(fibonacci(6)) # 输出8
栈的操作
栈是一种线性数据结构,遵循后进先出(LIFO)原则。以下是一些常见的栈操作:
压入(Push):可以将元素压入栈顶,即在栈的顶部添加一个新元素。
弹出(Pop):可以通过执行弹出操作将栈顶元素移除,即移除最后压入栈的元素。
窥视(Peek):可以使用窥视操作查看栈顶元素而不将其移除。
是否为空(IsEmpty):可以检查栈是否为空。
大小(Size):可以通过大小操作确定栈中的元素数量。
这些是栈上最常见的操作。具体的操作和算法可能会根据问题的需求和所使用的编程语言有所不同。栈常用于评估表达式、实现程序中的函数调用栈等许多应用中。
栈在现实生活中的应用
栈的一个现实生活中的例子是餐盘堆叠的层次结构。当你从堆叠中取出一个盘子时,你只能拿到最上面的那个盘子,而这正是最近添加到堆叠中的盘子。如果你想要堆叠底部的盘子,必须先移除上面的所有盘子才能到达它。
浏览器使用栈数据结构来记录之前访问过的网站。 手机中的通话记录也使用了栈数据结构。
2.4 队列
队列是一种线性数据结构,遵循特定的操作顺序,即先入先出(FIFO)的原则。也就是说,最先存储的数据项将最先被访问。在队列中,数据的进入和取出不是在同一端进行的。队列的一个例子是消费者排队等待资源的情况,其中最先到达的消费者将最先得到服务。
在队列上可以执行各种操作,比如反转队列(使用或不使用递归)、反转队列的前K个元素等。队列中常见的基本操作包括入队(enqueue)、出队(dequeue)、查看队首元素(front)、查看队尾元素(rear)等。
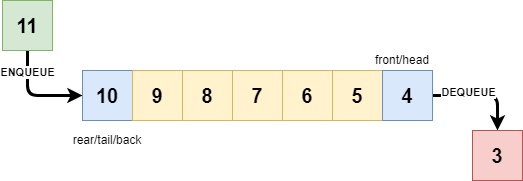
队列的特性
队列具有以下各种不同的特性:
队列是一个先入先出(FIFO)结构。
要移除队列中的最后一个元素,必须先移除队列中在该元素之前插入的所有元素。
队列的实现通常基于数组或链表。对于数组实现的队列,出队操作通常只会移动队首指针,而不改变内存中数据的位置。在环形队列的实现中,队首指针在一定范围内循环,这样避免了频繁的数据移动。
队列是一个相同数据类型元素的有序列表。
队列的应用
队列的不同应用如下:
队列用于处理网站流量。
它有助于维护媒体播放器中的播放列表。
队列用于操作系统中处理中断。
它有助于为单个共享资源提供服务,比如打印机、CPU任务调度等。
队列用于异步数据传输,例如管道、文件IO和套接字。
队列用于操作系统中的作业调度。
在社交媒体中,队列用于上传多张照片或视频。
队列数据结构用于发送电子邮件。
队列用于在处理网站流量时同时管理多个请求。
在Windows操作系统中,队列用于切换多个应用程序。
队列的操作
队列是一种线性数据结构,实现先进先出 (FIFO) 原则。以下是对队列执行的一些常见操作:
Enqueue :可以将元素添加到队列的后面,将新元素添加到队列的末尾。
Dequeue :可以通过执行出队操作从队列中删除前面的元素,从而有效地删除添加到队列中的第一个元素。
Peek :可以使用 peek 操作检查前面的元素,而无需将其从队列中删除。
IsEmpty :可以检查以确定队列是否为空。
Size :可以使用 size 操作确定队列中元素的数量。
队列在实际生活中的应用
世界中的队列示例是单车道单向道路,先进入的车辆将先退出。
更真实的例子可以在售票窗口的队列中看到。
商店中的收银队伍也是队列的一个示例。
自动扶梯上的人们
2.5 树
树是一种非线性的分层数据结构,其中元素以树状结构排列。在树中,最顶层的节点称为根节点。每个节点都包含一些数据,数据可以是任何类型。它由中心节点、结构节点和通过边连接的子节点组成。不同的树数据结构允许更快、更容易地访问数据,因为它是非线性数据结构。树有各种术语,如节点、根、边、树的高度、树的度等。
Binary Tree
二叉树数据结构是一种分层数据结构,其中每个节点最多有两个子节点,称为左子节点和右子节点。它通常用于计算机科学中,用于高效存储和检索数据,具有插入、删除和遍历等各种操作。
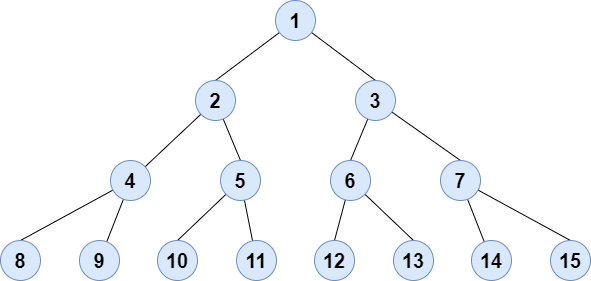
Binary Search Tree
二叉搜索树(简称BST)是一种特殊的二叉树,它具有以下特性:
若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
若任意节点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
任意节点的左、右子树也分别为二叉查找树。
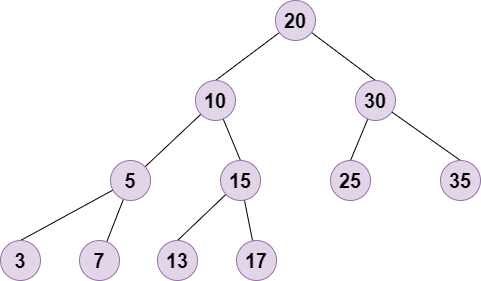
AVL Tree
AVL树是一种自平衡二叉搜索树(Binary Search Tree, BST),以其发明者G. M. Adelson-Velsky和E. M. Landis的名字命名。与普通的二叉搜索树不同,AVL树在每次插入或删除节点时,会进行必要的旋转操作,以确保树的高度差在左右子树之间不超过1,从而保证查找、插入和删除操作的时间复杂度始终为O(log_n)。
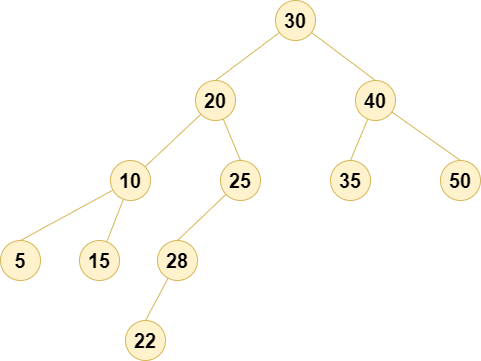
为了演示 AVL 树中的旋转操作,我们需要选择一个具体的插入顺序,使得树在插入某些节点后出现不平衡,然后通过旋转恢复平衡。我们将使用一个常见的场景——插入一个节点导致不平衡,然后执行旋转操作来恢复平衡。
旋转演示示例
假设我们先按以下顺序插入节点:30, 20, 40, 10, 25, 35, 50, 5, 15, 28。在插入这些节点后,树的结构如下:
30
/ \
20 40
/ \ / \
10 25 35 50
/ \
5 15现在,假设我们插入节点 22,插入后树的结构如下:
30
/ \
20 40
/ \ / \
10 25 35 50
/ \ /
5 15 22分析平衡性
节点 20 的左子树高度为 2(节点
10),右子树高度为 2(节点25)。节点 25 的左子树高度为 1(节点
22),右子树高度为 0(无节点)。
现在插入 22 后,节点 20 的左子树高度为 2(节点 10),右子树高度为 3(节点 25 -> 22),导致节点 20 的平衡因子变为 -1,这还在 AVL 树允许的范围内。但在更进一步插入 28 后,情况就会不同。
插入 28 导致不平衡
插入 28 后,树的结构变成:
30
/ \
20 40
/ \ / \
10 25 35 50
/ \ / \
5 15 22 28节点 25 的左子树高度为 1(节点
22),右子树高度为 1(节点28),平衡因子为 0,仍然平衡。节点 20 的左子树高度为 2(节点
10),右子树高度为 3(节点25),平衡因子为 -1,仍然平衡。节点 30 的左子树高度为 4(节点
20),右子树高度为 2(节点40),平衡因子为 2,不平衡,需要进行旋转。
右旋操作(Right Rotation)
右旋(Right Rotation)是 AVL 树中的一种基本操作,用于恢复树的平衡。右旋操作的目的是将不平衡的节点向右旋转,使得左子树变成新的子树根节点,从而减少树的高度。
为了恢复平衡,需要对节点 30 进行右旋操作:
25
/ \
20 30
/ \ / \
10 22 28 40
/ \ / \
5 15 35 50旋转后的树
旋转后,节点 25 变成新的根节点,树的结构恢复了平衡:
根节点 25:左子树高度为 3,右子树高度为 3,平衡。
节点 20 和 节点 30:左子树和右子树的高度差都在1以内,平衡。
通过这个旋转操作,AVL 树恢复了平衡,并继续保持二叉搜索树的性质。
B-tree
传统二叉搜索树的局限性可能令人沮丧。 B 树是一种多才多艺的数据结构,可以轻松处理大量数据。当涉及到存储和搜索大量数据时,传统的二叉搜索树由于其性能差和内存使用率高而变得不切实际。 B 树,也称为 Balance Tree,是一种自平衡树,专门为克服这些限制而设计。
与传统的二叉搜索树不同,B 树的特点是可以在单个节点中存储大量键,这就是为什么它们也被称为Large Key Tree, B 树中的每个节点可以包含多个键,这使得树具有更大的分支因子,从而具有更浅的高度。这种浅高度会减少磁盘 I/O,从而加快搜索和插入操作的速度。B 树特别适合具有缓慢、大量数据访问的存储系统,例如硬盘驱动器、闪存和 CD-ROM。
B 树通过确保每个节点具有最少数量的键来保持平衡,因此树始终是平衡的。这种平衡保证了插入、删除和搜索等操作的时间复杂度始终为 O(log n),无论树的初始形状如何。
B树的特点
所有叶子都处于同一层。
B 树由术语最小度(
mini degree)t定义。t的值取决于磁盘块大小。除根之外的每个节点必须至少包含
t-1个键(key,用于存放数据或者指向数据)。根可能至少包含1个键。所有节点(包括根节点)最多可以包含 (
2t-1)个key节点的子节点数量等于其中的键数量加1 。
节点的所有键均按升序排序。两个键
k1和k2之间的子键包含k1和k2范围内的所有键。B 树从根开始生长和收缩,这与二叉搜索树不同。二叉搜索树向下生长,也向下收缩。
与其他平衡二叉搜索树一样,搜索、插入和删除的时间复杂度为 O(log n)。
B 树中节点的插入仅发生在叶节点上。
阶(order)与最小度的区别
在B树(B-tree)中,“阶”(order)或称为“度”(degree),通常是指树中节点的最大子节点数。这个概念有时会与“最小度数”相混淆,因此需要明确区分。
阶(Order)的定义
阶(order) 通常定义为B树中一个节点所能拥有的最大子节点数。它规定了树的结构,影响了节点的关键字数量以及树的深度。
具体来说:
如果一棵B树的阶为 ( m ),那么:
一个节点最多可以有 ( m ) 个子节点。
一个节点最多可以存储 ( m-1 ) 个关键字。
一个节点至少要有 [\frac{m}{2}] 个子节点(根节点例外,至少有2个子节点)。
一个节点至少要有 \lceil \frac{m}{2} \rceil - 1 个关键字(根节点例外,至少有1个关键字)。
阶与最小度数的关系
有时候B树的“最小度数” ( t ) 与“阶” ( m ) 之间的关系可以表述为:阶 ( m = 2t )。因此:
最小度数 ( t ) 定义了每个节点的最小子节点数,即节点至少要有 ( t ) 个子节点。
阶 ( m ) 定义了每个节点的最大子节点数,即节点最多可以有 ( 2t = m ) 个子节点。
例子
如果你有一棵阶为 4 的 B 树:
每个节点最多可以有 4 个子节点,最多存储 3 个关键字。
每个节点至少要有 \lceil 4/2 \rceil = 2 个子节点,至少要有 ( 2 - 1 = 1 ) 个关键字(对于非根节点)。
总结
阶(order) 是指B树中节点可以拥有的最大子节点数。
最小度数(minimum degree) 是指节点必须拥有的最小子节点数,并且与阶有直接的关系,通常 ( t = m/2 )。
理解这两个概念有助于正确地构建和分析B树的数据结构。
B树如此重要,因此需要连接一下它的各种操作
当然,我可以举一个简单的例子来说明B树的插入、删除、更新和查询操作。为了便于理解,假设我们使用一棵最小阶数 ( t = 2 ) 的B树。
插入操作
假设我们从空树开始,依次插入以下关键字:10, 20, 5, 6, 12, 30, 7, 17。
步骤1: 插入 10, 20, 5
树开始为空,插入10:
[10]插入20,20比10大,所以放在10的右边:
[10, 20]插入5,5比10小,所以放在10的左边:
[5, 10, 20]
步骤2: 插入 6, 12, 30
插入6,6比5大但比10小,插入在5和10之间:
[5, 6, 10, 20]插入12,12比10大但比20小,插入在10和20之间:
[5, 6, 10, 12, 20]插入30,根节点已经满了(5个关键字),需要分裂。中间关键字10被提升为新的根节点,左右分裂成两个子节点:
[10] / \ [5, 6] [12, 20, 30]
步骤3: 插入 7, 17
插入7,7比6大比10小,放在左子节点中合适位置:
[10] / \ [5, 6, 7] [12, 20, 30]插入17,17比12大但比20小,插入在右子节点的合适位置:
[10] / \ [5, 6, 7] [12, 17, 20, 30]
查询操作(二分查找)
要在B树中查询关键字,我们从根节点开始,根据关键字的大小来逐层导航:
查询17:
从根节点[10]开始,17比10大,进入右子节点[12, 17, 20, 30]。
在右子节点中找到17,查询成功。
查询8:
从根节点[10]开始,8比10小,进入左子节点[5, 6, 7]。
在左子节点中没有找到8,查询失败。
更新操作
更新12为15:
首先查找12的位置:它在右子节点[12, 17, 20, 30]中。
将12替换为15:
[10] / \ [5, 6, 7] [15, 17, 20, 30]
删除操作
删除关键字20:
首先找到20的位置:在右子节点[15, 17, 20, 30]中。
删除20,简单地从节点中移除它:
[10] / \ [5, 6, 7] [15, 17, 30]
删除根节点10(更复杂的情况):
删除根节点10后,左子节点的最大关键字(7)或右子节点的最小关键字(15)会提升为新的根节点。
假设我们提升右子节点的最小关键字15为新的根节点:
[15] / \ [5, 6, 7] [17, 30]
Heap
堆是一种特殊的基于树的数据结构,其中树是一个完全二叉树。一般来说,堆可以分为两种类型:
大顶堆(Max-Heap):在大顶堆中,根节点上的键值必须是所有子节点中最大的。同样的性质必须在二叉树的所有子树中递归地成立。
插入 10, 20, 15, 30, 40 ,结果如下
40 / \ 30 15 / \ 20 10 小顶堆(Min-Heap):在小顶堆中,根节点上的键值必须是所有子节点中最小的。同样的性质必须在二叉树的所有子树中递归地成立。
同上,同样的数据和顺序插入小顶堆
10 / \ 20 15 / \ 30 40
Heap主要用于一些堆排序,时间复杂度为 O(nlogn),还有一些有限队列,任务调度,压缩用的霍夫曼树等。图算法中heap用于寻找最小生成树(Prim算法),Dijkstra最短路径算法的优先队列则是Heap实现,用于减少复杂度的。
此外,还有许多特殊的树形,比如Trie,经典的红黑树,篇幅有限就不一一介绍了。
2.6 图
最后说说图,graph。graph图论源于七桥问题和欧拉大神,这种数据结构也目前非常火热的人工智能的一个分项,机器学习性能和参数数量不是线性的,往往参数过大时,收益往往更小了,所以目光就转移到了图计算方向了,而图这种数据结构是基础。
图是一种数据结构,由边连接的节点(顶点)集合组成。图用于表示对象之间的关系,广泛应用于计算机科学、数学等领域。图可用于对各种现实世界系统进行建模,例如社交网络、交通网络和计算机网络。
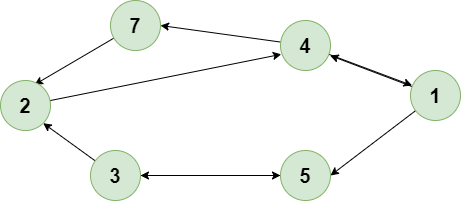
图的特性:
图具有以下不同的特性:
偏心率:从一个顶点到所有其他顶点的最大距离被称为该顶点的偏心率。
中心点:具有最小偏心率的顶点被视为图的中心点。
半径:所有顶点中偏心率的最小值被认为是连通图的半径。
图的应用:
图的不同应用如下:
图用于表示计算的流程。
它用于图的建模。
操作系统使用资源分配图(Resource Allocation Graph)。
还用于万维网(World Wide Web),其中网页表示节点。
图上的操作:
图是一种由节点和边组成的非线性数据结构。以下是图上常见的操作:
添加顶点:可以将新顶点添加到图中以表示一个新节点。
添加边:可以在顶点之间添加边以表示节点之间的关系。
移除顶点:可以通过更新相邻顶点的引用以移除当前顶点的引用,从图中移除顶点。
移除边:可以通过更新相邻顶点的引用以移除当前边的引用,从图中移除边。
深度优先搜索(DFS):可以使用深度优先搜索以深度优先的方式遍历图中的顶点。
广度优先搜索(BFS):可以使用广度优先搜索以广度优先的方式遍历图中的顶点。
最短路径:可以使用如Dijkstra算法或A*算法等算法确定两个顶点之间的最短路径。
连通分量:可以通过找到图中相互连通但不与其他顶点连通的顶点集来确定图的连通分量。
环检测:可以通过在深度优先搜索期间检查回边来检测图中的环。
这些是图上最常见的一些操作。具体操作和算法可能会根据问题的要求和所使用的编程语言而有所不同。图广泛用于计算机网络、社交网络和路由问题等应用中。
图的实际应用:
图的最常见的现实例子之一是Google Maps,在那里城市作为顶点,连接这些顶点的路径作为图的边。 社交网络也是图的一个现实例子,其中网络上的每个人都是一个节点,他们在网络上的所有友谊是图的边。 图还用于研究物理和化学中的分子。知识图谱结合图数据库进行推理也是目前图应用的一个热门方向。

