串联 RLC 电路分析
串联 RLC 电路由一个电阻、电容和电感串联连接在交流电源上。
到目前为止,我们已经看到,当把三种基本无源元件——电阻(Resistance)、电感(Inductance)和电容(Capacitance)——连接到正弦交流电压时,它们之间的相位关系有很大差异。但我们可以将这些无源元件串联,形成一个串联 RLC 电路,并将其与交流电源相连。
在纯欧姆电阻中,电压波形与电流同相;
在纯电感中,电压波形超前电流 90°,因此记作 ELI;
在纯电容中,电压波形滞后电流 90°,因此记作 ICE。
这个相位差 \theta取决于所用元件的电抗值(reactance, X)
当元件为电阻性时 X=0;
为电感性时 X>0;
为电容性时 X<0
从而它们的阻抗(impedance, Z)分别为:
元件阻抗
与其分别分析每个无源元件,我们可以将三者组合成一个串联 RLC 电路。串联 RLC 电路的分析与之前研究的串联 RL 和串联 RC 电路相同,只不过这一次需要同时考虑 X_L 和 X_C 的幅值,以求得整个电路的总电抗。串联 RLC 电路被归为二阶电路second-order,因为它包含两个储能元件:电感 L 和电容 C。下面考虑下图所示的 RLC 电路:
串联RLC电路
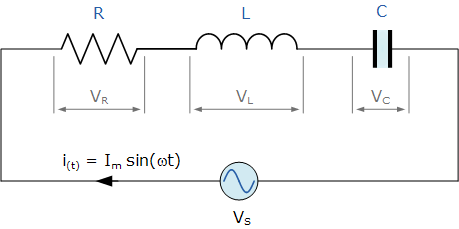
上图所示的串联 RLC 电路只有一个回路,流经电路的瞬时电流在每个元件中均相同。由于电感和电容的电抗 X_L 和 X_C 都随电源频率 f 而变化,串联 RLC 电路的正弦响应也会随频率改变。因此,流过电阻 R、电感 L 和电容 C 各元件的电压降在相位上会出现如下差异:
纯电阻上的瞬时电压 V_R 与电流“同相”
纯电感上的瞬时电压 V_L 相对于电流“超前”90°
纯电容上的瞬时电压 V_C 相对于电流“滞后”90°
因此, V_L 与 V_C 相位相差180°,彼此相互抵消
对于上述串联 RLC 电路,其相量示意可表示为:
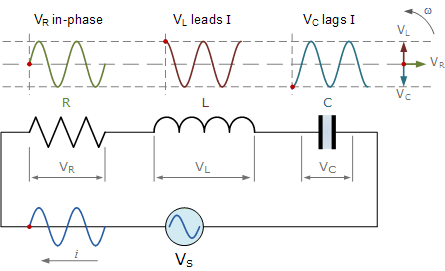
在串联 RLC 电路中,电源电压的幅值由三个元件上的电压—— V_R、V_L 和 V_C 组成,且三者共用同一电流。因此,在矢量图中以电流矢量为参考,将三个电压矢量分别相对于该参考绘制,如下所示:
各电压矢量
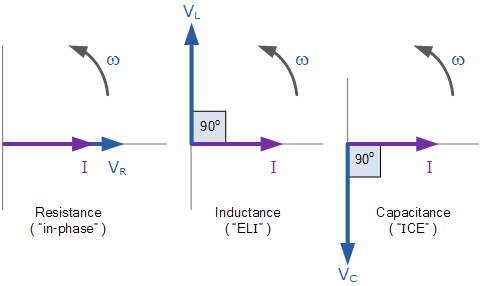
这就意味着,我们不能简单地将 V_R、V_L 和 V_C 相加来得到跨在这三种元件上的电源电压 V_S,因为这三者的电压矢量相对于电流矢量指向不同的方向。因此,我们必须将这三个元件的电压矢量以相量形式矢量相加,才能得到电源电压 V_S。
基尔霍夫电压定律(KVL)对回路和节点电路均适用,它指出:在任何闭合回路中,各电压降之和等于电动势之和。将此定律应用于上述三个电压,就能求得电源电压 V_S 的幅值。
串联 RLC 电路的瞬时电压
串联 RLC 电路的相量图是将上述三个独立的相量组合起来,并以矢量方式相加这些电压而得到的。由于流过电路的电流在三个元件中相同,因此可将电流相量作为参考矢量,并按照各自的相位角在参考矢量的基础上绘制三个电压相量。
得到的电源电压相量 V_S,可先将两个电压相量 V_L 和 V_C 矢量相加,再将此合成矢量与剩余的电压相量 V_R 相加。 V_S 与电流 i 之间形成的角度即为电路的相位角,如下所示。
串联 RLC 电路的相量图
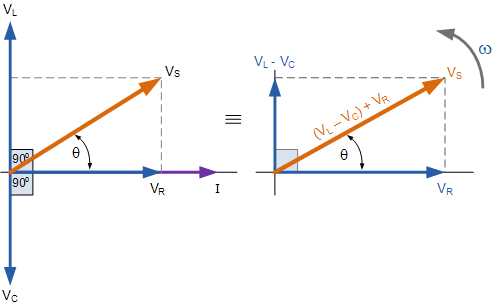
从上图右侧的相量图可以看出,电压矢量构成了一个直角三角形,其中斜边为 V_S,水平轴为 V_R,垂直轴为 V_L - V_C。希望你能注意到,这正是我们熟悉的电压三角形,因此我们可以在这个电压三角形上应用勾股定理,来数学地求出 V_S 的值,如下所示。
串联 RLC 电路的电压三角形
请注意,在使用上述方程时,最终的无功电压必须始终为正值,也就是说应始终用较大的电压减去较小的电压;我们不能将负电压加到 V_R 上,所以写成 V_L - V_C 或 V_C - V_L 都是正确的,前提是要用较大的值减去较小的值,否则计算出的 V_S 将不正确。(也就是绝对值的意思)
如上所述,在串联 RLC 电路中,电流在所有元件中的幅值和相位均相同。因此,每个元件上的电压也可以根据流过的电流,用数学形式表示为:
通过将这些值代入上述电压三角形的勾股定理公式,我们将得到:
由此可见,电源电压的幅值与流过电路的电流幅值成正比。这个比例常数称为电路的阻抗(Impedance),它最终取决于电阻 R 以及电感和电容的电抗 X_L 和 X_C。
在上述串联 RLC 电路中,电流所受的总阻抗由三部分组成: X_L、X_C 和 R。任意串联 RLC 电路的总无功电抗 X_T 定义为:
因此,电路的总阻抗可视为驱动电流流过该电路所需的电压与电流之比。
串联 RLC 电路的阻抗
由于三个电压矢量彼此错相, R、X_L 和 X_C 之间也必须错相,其关系即这三者的矢量和。通过矢量相加可得到电路的总阻抗 Z。这些阻抗可以用阻抗三角形来表示,如下所示:
串联 RLC 电路的阻抗三角形
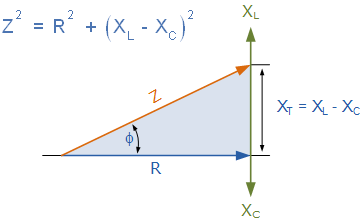
串联 RLC 电路的阻抗 Z 与角频率 \omega 有关,电感电抗 X_L 和电容电抗 X_C 亦是如此。如果电容电抗大于电感电抗( X_C > X_L),则电路的总体电抗呈电容性,产生超前相位角。
同样地,如果电感电抗大于电容电抗( X_L > X_C),则总体电抗呈电感性,使串联电路产生滞后相位角。当两者电抗相等( X_L = X_C)时,发生这种情况的角频率称为共振频率,在此会产生共振resonance效应,我们将在另一个教程中更详细地讨论。
因此,电路中电流的幅值取决于施加于串联 RLC 电路的频率。当阻抗 Z 达到最大时,电流为最小;反之,当阻抗 Z 达到最小时,电流为最大。于是,上述阻抗公式可以重写为:
电源电压 V_S 与电流 i 之间的相位角 \theta,与阻抗三角形中 Z 与 R 之间的角度相同。该相位角可为正或负,取决于电源电压是领先还是滞后于电路电流,并可根据阻抗三角形的欧姆值,通过以下数学公式计算:
串联RLC电路示例1
一个串联 RLC 电路,包含一个 12 Ω 的电阻、0.15 H 的电感和 100 μF 的电容,连接在一个 100 V、50 Hz 的交流电源上。计算该电路的总阻抗、流过电路的电流、功率因数,并绘制电压相量图。
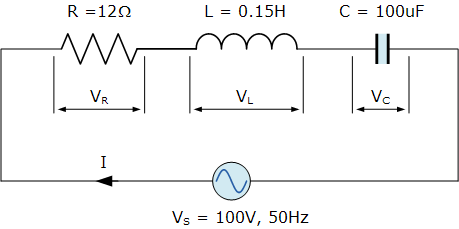
电感电抗:
电容电抗:
总阻抗:
电路电流:
各元件电压幅值:
功率因数与相位角:
相位图:
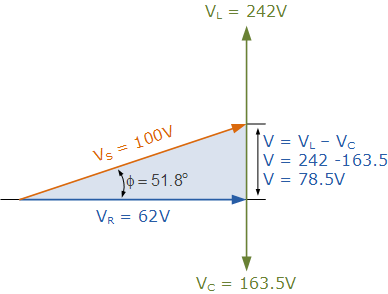
由于相位角 \theta 被算作正值 51.8^\circ,电路的总体电抗必定是电感性的。因为在串联 RLC 电路中我们已将电流矢量作为参考矢量,所以电流相比电源电压落后 51.8^\circ,相位角为滞后,这也正符合我们的助记 “ELI”。
总结
在包含电阻 R、电感 L 和电容 C 的串联 RLC 电路中,电源电压 V_S 是由三个分量 V_R、V_L 和 V_C 的相量和构成,三者共用同一电流 I。
由于电流 I 在所有元件中相同,因此在绘制电压三角形时,电流相量被用作水平参考轴。
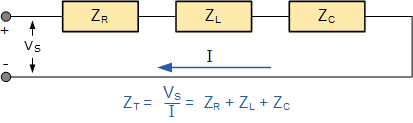
电路的阻抗 Z 表示对电流流动的总阻碍。对于串联 RLC 电路,可通过将电压三角形的各边除以电流 I 来得到对应的阻抗三角形:
电阻元件上的电压降为 I\times R,
两个无功元件上的电压净降为 I\times X = I\,X_L - I\,X_C,
电源电压为 I\times Z。 三角形中 V_S 与 I 之间的角度即为相位角 \theta。
如果串联 RLC 电路中包含多个纯或非纯的电阻、电容或电感元件,则可以将同类元件合并成一个等效元件。例如:
R_T = R_1 + R_2 + R_3 + \dots,\quad L_T = L_1 + L_2 + L_3 + \dots这样就能将包含多个元件的复杂电路简化为一个等效阻抗。
在下一个关于并联 RLC 电路的教程中,我们将研究这三个元件以并联电路方式连接时,在施加稳态正弦交流波形时的电压–电流关系,并给出相应的相量图表示。我们还将首次引入导纳(Admittance)的概念。
附件
二阶电路
“二阶电路”指的是其描述方程(电压或电流的微分方程)的阶数为 2 的电路。通俗地说,它具有两个独立的储能元件( L 和 C),因此其动态特性由二阶常微分方程来描述。主要特点有:
储能元件个数 串联
RLC电路中既有一个电感 L,又有一个电容 C,总共两个储能元件。微分方程阶数 应用基尔霍夫电压定律后,会得到包含二阶导数项(来自 L)和一阶导数项(来自 R)、以及零阶项(来自 C)的二阶常微分方程:
L\,\frac{d^2i}{dt^2} + R\,\frac{di}{dt} + \frac{1}{C}\,i = v_{\text{in}}(t)自然响应特性 二阶系统的自然响应一般由两个指数(或一对复共轭极点)决定,可能是过阻尼、临界阻尼或欠阻尼三种情况。
频率响应 二阶电路的频率响应会出现共振峰,中心频率 \omega_0 = \tfrac{1}{\sqrt{LC}},品质因数 Q = \tfrac{\omega_0 L}{R}。
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

