交流电容与容抗
AC Capacitance and Capacitive Reactance
在交流电容器中,阻碍电流流动的量称为容抗Capacitive Reactance,而容抗与电源频率成反比。
电容器在其导电极板上以电荷的形式储存能量。存储在电容器中的电荷量 Q 与极板间的电压成线性正比。因此,当电容器连接到正弦交流电源时,其交流电容(AC capacitance)就是衡量它储存电荷能力的指标。
当电容器接在直流电源上时,它会以由其时间常数决定的速率充电,直到充至所加电压的值为止;只要电源电压持续存在,电容器就能无限期地保持这一电荷。
在这一充电过程中,充电电流 i 流入电容器,该电流受到电压变化率的阻碍,其大小等于极板上电荷变化率。因此,电容器对流入其极板的电流具有阻抗。
这一充电电流与电容器电压变化速率之间的关系可用数学式表示为:
其中 C 为电容值(单位:法拉), \frac{dv}{dt} 是电源电压随时间的变化率。一旦电容器“充满”电荷,极板饱和,不再允许更多电子流入,此时电容器便成为一个临时的存储装置。
纯电容器在其极板上能无限期地保持电荷,即使直流电源电压被移除也是如此。然而,在含有“交流电容”的正弦电压电路中,电容器会以与电源频率相同的速率交替充电和放电。因此,在交流电路中,电容器实际上是在不断地进行充放电。
当将交变正弦电压施加到交流电容器的极板上时,电容器先朝一个方向充电,然后再在与交流电源电压变化速率相同的频率下反向充电,其极性随之相应改变。这种电容两端电压的瞬时变化,会受到将电荷沉积(或释放)到极板上所需时间的制约,其关系由
给出。请参考下图所示电路:
具有正弦电源的交流电容
AC Capacitance with a Sinusoidal Supply
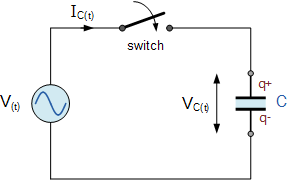
当开关闭合时,由于在 t = 0 时电容极板上尚无电荷,一股很大的电流将瞬间流入电容器。此时正弦电源电压 V 正以最大变化率向正方向上升,正好越过零参考轴,即在 0° 处。由于极板间电压变化率此刻达到最大值,电流流入电容的速率也达到最大,此时最多量的电子正从一极板移动到另一极板。
当正弦电源电压到达波形的 90° 点时,上升速率开始减缓,并在极短时间内电容两端电压既不增加也不减少,因此电流降为零,因为此刻没有电压变化率可驱动电流。
在90° 点,电容两端的电压达到最大值 V_{\text{max}},此时电容已完全充电,极板上的电子饱和,因而无电流流入。
在此瞬间之后,电源电压开始向负方向下降,朝向 180° 的零参考线移动。虽然电源电压仍为正,但为了维持电压连续性,电容开始释放部分过剩的电子回到另一极板,这导致电容电流反向,流向负方向。
当电源电压波形在 180° 处再次越过零参考轴时,正弦电压的变化率(斜率)在负方向上达到最大,因此此刻流入电容的电流也在负方向上达到最大。同时,在 180° 点,极板间的电压为零,因为两个极板上储存的电荷量相等。
在首个半周(0° 到 180°)内,所加电压达到最大正值的时刻,比电流达到最大正值晚了四分之一周期(即 \tfrac{1}{4}ƒ),换言之,施加于纯电容电路的电压相对于电流“滞后”四分之一周期或 90°,如下面所示。
交流电容的正弦波形
Sinusoidal Waveforms for AC Capacitance
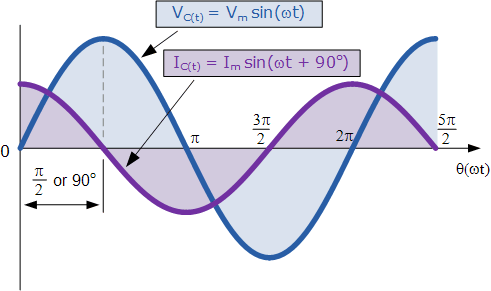
在半个周期的后半段(180° 到 360°),电源电压反向,朝其负峰值(270°)变化。此时,电容两端的电位差既不增加也不减少,因此电流降至零。电容两端的电压达到其最大负值,此时没有电流流入电容,电容已完全充电,与 90° 时的状态相同,但方向相反。
当负向电源电压开始向正方向上升,朝零参考线的 360° 点运动时,已充满电荷的电容为了维持电压连续性,需要释放部分过剩的电子,于是开始放电,直到电源电压在 360° 处再次降至零,充放电过程重新循环。
从上述电压和电流波形及描述可以看出,由于电容器的充放电过程,电流始终比电容两端的电压超前四分之一周期,即 \pi/2(90°)的“相位差”。因此,在交流电容电路中,电压与电流的相位关系正好与上一节中讨论的交流电感相反。
这一效应也可以用相量图来表示:在纯电容电路中,电压“滞后”电流 90°。但如果以电压为参考,则可以说电流“超前”电压四分之一周期(90°),如下面的向量图所示。
交流电容的相量图
Phasor Diagram for AC Capacitance
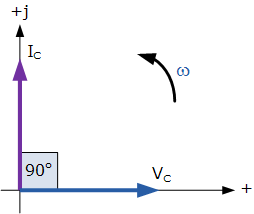
对于纯电容器, V_C 相对于 I_C 滞后 90°,或者我们也可以说 I_C 超前 V_C 90°。
记忆纯交流电容电路中电压与电流的相位关系,有多种方法,其中一个非常简单、易于记忆的助记法是“ICE”——
I(Current,电流)
C(Capacitance,电容)
E(Electromotive force,电动势/电压)
也就是说,在电容电路中电流先于电压,按顺序记作 I、C、E,无论电压起始相位如何,这个表达式在纯交流电容电路中始终成立。
容抗(Capacitive Reactance)
至此我们已知,电容器在其极板上对电压变化的抵抗,是通过电子在极板之间的充放电实现的,其电流大小与电压变化率成正比。与电阻器中用“电阻”来描述对电流的阻碍不同,电容器中对电流的阻碍称为“容抗”(Reactance),符号为 X,单位同样是欧姆( \Omega),以区别于用 R 表示的纯电阻。
由于电容器的充放电速度取决于两端电压的变化速率
电压变化越快,电流越大;
电压变化越慢,电流越小
因此,在交流电路中,电容的容抗与电源频率成反比,频率越高,容抗越小;频率越低,容抗越大。根据这个特性可以确定电容器作用
容抗公式
其中:
X_C 为容抗,单位为欧姆( \Omega);
f 为频率,单位为赫兹( Hz);
C 为交流电容,单位为法拉( F)。
在处理交流电容时,也可以用弧频来定义容抗,其中欧米伽 \omega 等于 2\pi f。
从上述公式可以看出
随着频率的增大,容抗及其总阻抗(单位:Ω)会逐渐减小并趋近于零,表现得像短路。
反之,当频率趋近于零或直流时,容抗会增大并趋于无穷大,表现得像开路,这也正是电容器阻断直流的原因。
容抗与频率的关系正好与上一节中讲到的感抗( X_L)相反。因此,容抗与频率“成反比”,在低频时取值较大,在高频时取值较小,如下所示。
容抗与频率的关系
Capacitive Reactance against Frequency
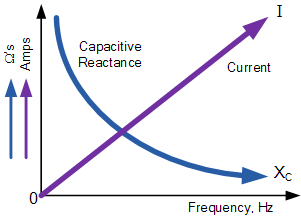
电容器的容抗随着极板之间电压频率的增加而减小。因此,容抗与频率成反比。容抗虽会阻碍电流流动,但极板上的静电电荷(即其交流电容值)保持不变。
这意味着在每个半周期内,电容器更容易完全吸收极板上电荷的变化。同时,随着频率的提高,流入电容器的电流值也会增大,因为两端电压的变化速率加快。
我们可以如下展示在极低频和极高频下,纯交流电容的容抗变化:
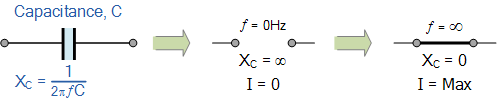
在包含纯电容的交流电路中,流入电容器的电流(电子流)可表示为:
其中
因此
若记最大电流为
且容抗
则有
因此,流入交流电容的有效值电流可定义为:
其中: I_C = \dfrac{V}{1/(\omega C)}(或 I_C = \dfrac{V}{X_C})是电流的幅值, \theta = +90^\circ 表示电压与电流之间的相位差或相位角。对于纯电容电路, I_C 超前 V_C 90°,或 V_C 滞后 I_C 90°。
相量域
在相量域中,交流电容两端的电压将表示为:
相量域 在相量域中,交流电容两端的电压为:
其中
即该电容的阻抗 Z。
在极坐标形式中,这可表示为: X_C\angle -90^\circ,其中:
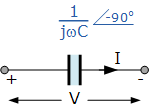
在极坐标形式下,容抗可表示为:
串联 R + C 电路中的交流特性
如上所述,在纯交流电容中,流入电容的电流比电压超前 90°。但在现实中,不可能存在完全纯粹的交流电容器,因为所有电容器的极板之间都会存在一定的内部电阻,从而产生泄漏电流leakage current。
因此,我们可以将电容器等效为一个电阻 R 与电容 C 串联的“杂散电容”(impure capacitor)。
当电容器具有“内部”电阻时,就需要把它的总阻抗表示为一个与电容串联的电阻。在含有电容 C 与电阻 R 的交流电路中,整个组合上的电压相量 V 就等于电阻两端电压相量 V_R 与电容两端电压相量 V_C 的相量和。
这意味着,流入该串联组合的电流依然超前电压,但超前量小于 90°,其具体数值由 R 与 C 的大小决定,并用希腊字母 φ(phi)表示两者之间的相位角。
下图所示为一个简单的串联 RC 电路,其中一个欧姆电阻 R 与一个纯电容 C 串联连接。
串联电阻–电容电路
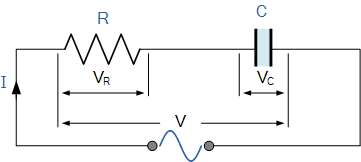
在上述串联 RC 电路中,我们可以看到流入电路的电流对电阻和电容而言是相同的,而电压则由两个分量电压 V_R 和 V_C 组成。
这两个分量的合成电压可以通过数学方法求得,但由于向量 V_R 与 V_C 存在 90° 的相位差,因此需要通过构建向量图来进行矢量相加。
要绘制交流电容的向量图,必须先确定一个参考或公共分量。在串联交流电路中,电流是公共的,因此可以用作参考源,因为相同的电流既流过电阻又流入电容。下面分别给出了纯电阻和纯电容的单独向量图:
两种纯元件的向量图
Vector Diagrams for the Two Pure Components
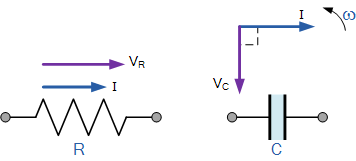
对于交流电阻,电压和电流向量同相,因此将电压向量 VR 按相同比例叠加绘制在电流向量上。
同时,我们知道在纯交流电容电路中,电流超前电压(ICE),因此将电容电压向量 V_C 在电流向量之后滞后 90°,并按与 V_R 相同的比例绘制,如下所示。
合成电压的向量图
Vector Diagram of the Resultant Voltage
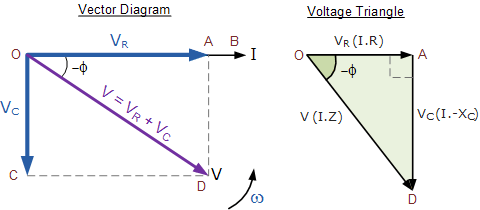
在上方的向量图中,OB 线表示水平的电流参考,OA 线表示与电流同相的电阻分量电压。OC 线表示滞后于电流 90° 的电容分量电压,因此仍能看出电流超前纯电容电压 90°。OD 线则表示合成后的电源电压。
由于在纯电容中电流超前电压 90°,由各分量电压 VR 和 VC 绘制的合成相量图便形成了如图中 OAD 所示的直角电压三角形。接着,我们可以使用勾股定理来计算这一串联 RC 电路上合成电压的数值。
因为 V_R = I \cdot R,\quad V_C = I \cdot X_C,所以所加电压即这两者的向量和,如下所示:
在串联 RC 电路中,总电压满足勾股定理:
又
代入得
两边开方后:
因此,电路中的电流为:
其中 Z=\sqrt{R^2+X_C^2} 为该串联电路的总阻抗impedance。
交流电容的阻抗
阻抗 Z(单位:欧姆,Ω)是包含电阻(实部)和容抗(虚部)的交流电路对电流的“总”阻碍。纯电阻阻抗的相角为 0°,纯电容阻抗的相角为 –90°。
然而,当电阻与电容组合在同一电路中时,总阻抗的相角会根据两者的数值落在 0° 与 –90° 之间。上图所示的简单串联 RC 电路,其总阻抗可通过阻抗三角形来求得。
RC 阻抗三角形图
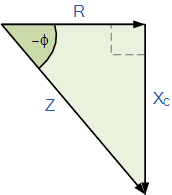
那么:
其中j表示 90° 的相位移。 这意味着,可以利用勾股定理来计算电压与电流之间的负相角 θ。
相角
Phase Angle
交流电容示例 1
一个单相正弦交流电源电压定义为: V(t)=240\sin\bigl(314t-20^\circ\bigr),该电源连接到一个纯交流电容 C=200\,\mu\text{F}。
求流入电容的电流值
绘制相应的相量图
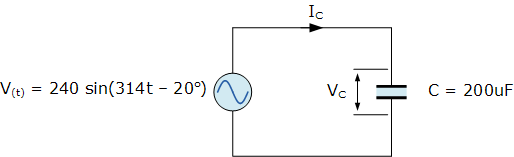
电容两端的峰值电压与电源电压相同。将该时域值转换为极坐标形式,得到:
容抗为:
然后,流入电容的最大瞬时电流可由欧姆定律求得:
由于在交流电容电路中电流比电压超前 90°,其相量图将如下所示:
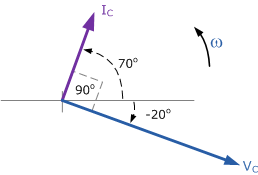
交流电容示例 2
一个具有 10 Ω 内部电阻和 100 μF 电容值的电容器,连接到电源电压 V(t) = 100 \sin(314t)上。
计算流入该电容的峰值瞬时电流。
绘制表示各分量电压降的电压三角形。
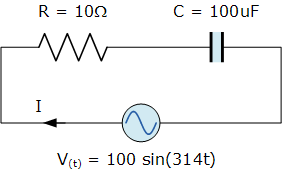
容抗和电路阻抗的计算如下:
容抗 X_C 和总阻抗 Z 的计算如下:
那么,流入电容器及整个电路的峰值电流表示为:
从上方的阻抗三角形可以计算出电流与电压之间的相位角,如下所示:
那么,电路中各元件的电压降可计算为:
那么,对于所计算的峰值,合成电压三角形将为:
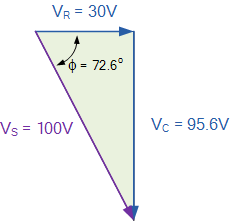
交流电容总结
在纯交流电容电路中,电压和电流“不同相”,电流比电压超前 90°,我们可以用助记“ICE”(I→C→E)来记忆:Current(电流)先于 Capacitance(电容),再到 Electromotive force(电动势/电压)。
电容器在交流电路中的等效阻抗称为阻抗 Z,它与频率相关;而电容的“容抗” X_C 则是其与频率的反比,定义为
到目前为止,我们已经看到,三种纯无源元件中电压与电流的相位关系各不相同:
电阻:相角 0^\circ;
电感:相角 +90^\circ;
电容:相角 -90^\circ。
在下一节关于串联 RLC 电路的教程中,我们将考察当三者串联并施加稳态正弦交流波形时的电压–电流关系,并给出相应的相量图表示。
附录
电容器作用
可以这么理解:电容在电路中利用它随频率变化的容抗特性,来对不同频率的信号产生不同的“通”或“阻”作用,从而在以下几个方面发挥“稳定”和“调节”作用:
滤波(Frequency Filtering)
在RC、LC 等滤波电路中,电容对低频(包括直流)表现为高阻,对高频表现为低阻。
低通滤波器(RC):串联电阻后接电容并接地,高频信号被电容“旁路”到地,只有低频留在输出;
高通滤波器(RC):电容串联在信号路径上,只有高频能通过,低频被阻断并旁路到地。 这样就能“稳定”地把我们想要的频段信号通过,把杂波或不需要的频率滤除。
耦合与隔直(AC Coupling / DC Blocking)
串联电容可以隔断直流分量,仅让交流信号通过,用于不同电路级之间的信号耦合,避免直流电位偏移。
电源去耦和平滑(Decoupling & Smoothing)
在电源线上并联大容量电容,可以快速吸收和释放电荷,平滑开关动作或负载突变引起的电压尖峰/凹陷,使输出电压更稳定,减少“电源纹波”。
谐振/定频(Resonance)
和电感 L 一起组成 LC 谐振电路,其谐振频率
f_0=\frac{1}{2\pi\sqrt{L\,C}}可以在该频率附近形成高增益或高阻抗,用于振荡器、频率选择电路。
总结来说,电容的“频率选择”特性(容抗随频率变化)使它能:
在信号处理电路中实现过滤、耦合、隔直;
在电源电路中平滑并稳定电压/电流;
在谐振电路中确定振荡或通带中心频率。
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

