交流电感与感抗

AC Inductance and Inductive Reactance

交流电感器对电流流动的阻碍称为感抗，其大小与电源频率成线性关系。

当接入交流电源时，流经电感线圈的电流会产生一个自感电动势self-induced emf，该电动势的方向与最初驱动电流的电动势相反。对于含有交流电感的时变电路而言，电感线圈表现为一种阻抗impedance ，限制线圈中时变电流的大小。

电感器和扼流圈本质上都是将导线绕制成线圈或环路，可绕在空心管架（空气芯）上，也可绕在铁磁材料（铁芯）上，以提高其电感量（称为电感）。

当在电感器两端施加电压时，电感器会在其周围产生磁场并以此形式存储能量。流经电感器的电流并非瞬间达到，而是受到电感器自身所产生的自感电动势（亦称反电动势）的制约。对于电感线圈而言，该反电动势 V_L 与流经线圈的电流变化率成正比。

随着时间推移，电流会不断上升，直到大约经历五个时间常数后达到最大稳态值steady state condition，此时自感反电动势已衰减至零。在这一稳态点，线圈中流动着恒定电流，不再产生阻碍电流的反电动势，因此线圈更类似于短路，允许运行最大电流通过。

然而，在含有交流电感的交流电路中，流经电感器的电流行为与在稳态直流电压下截然不同。在交流电路中，通过线圈绕组的电流所受的阻碍，不仅取决于线圈的电感量，还取决于所施加电压波形在由正向变为负向时的频率。

线圈中电流所受到的实际阻碍由线圈的交流阻抗决定，该交流阻抗以复数形式表示。但为了将直流电阻值与交流电阻值（即阻抗）区分开来，采用“电抗”一词。

与电阻一样，电抗的单位也是欧姆，用符号 X来区别纯电阻的 R值。由于这里讨论的元件是电感器，其电抗称为感抗（ X_L）Inductive Reactance，单位为欧姆。其数值可由下列公式求得。

感抗

Inductive Reactance

其中：

• X_L = 感抗，单位欧姆（Ω）

• \pi (pi) = 数值常数 3.142

• f = 频率，单位赫兹（Hz）

• L = 电感量，单位亨利（H）

我们也可以用弧度来定义感抗，其中角频率 \omega 等于 2\pi f。

当正弦电压施加到电感线圈上时，线圈产生的反电动势会抵抗电流的升降；对于一个纯电感（无电阻或损耗）的线圈，其阻抗（可表示为复数）就等于其感抗。此外，由于电抗既有大小又有方向（角度），因此可用向量来表示。请参见下图电路：

带正弦电源的交流电感

AC Inductance with a Sinusoidal Supply

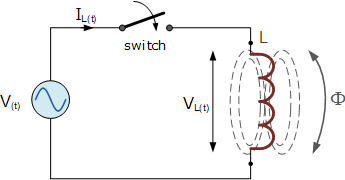
上述简单电路由一个纯电感 L 亨利（ H）构成，连接在下列正弦电压两端：

当开关闭合时，该正弦电压会驱动电流流过线圈，并由零上升到最大值。电流的这种上升或变化会在线圈内产生磁场，而该磁场又会反过来抵抗或限制电流的变化。

然而，在电流尚未像直流电路中那样达到最大值之前，电压就改变了极性，导致电流反向变化。由于线圈中的自感反电动势，这一反向变化再次受到延迟；在仅含纯电感的电路中，电流相对于电压延迟 90^\circ。

所施加的电压达到最大正值的时间，比电流达到最大正值的时间早四分之一周期（即 \tfrac{1}{4}f 周期）。换言之，施加在纯电感电路上的电压相对于电流超前四分之一周期，即 90^\circ，如图所示。

交流电感的正弦波形

Sinusoidal Waveforms for AC Inductance

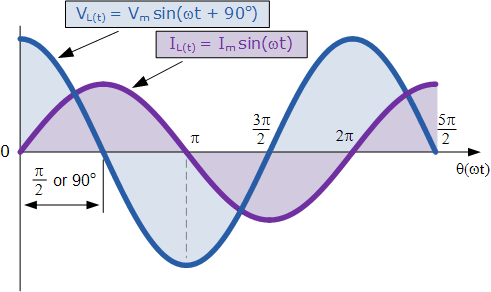
这种效应也可以用相量图表示：在纯电感电路中，电压“超前”电流 90^\circ。如果以电压为参考，我们也可以说电流相对于电压滞后四分之一周期（ 90^\circ），如下面的向量图所示。

交流电感相位图

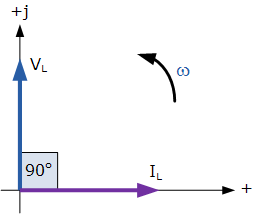
因此，对于一个理想无损电感器，电压 V_L 相对于电流 I_L 超前 90^\circ，或者也可以说电流 I_L 相对于电压 V_L 滞后 90^\circ。

有许多方法可以记忆纯电感电路中电压与电流的相位关系，但一个非常简单且易于记忆的方式是使用助记表达式“ELI”（读作 Ellie，如同女性名字）。

“ELI”代表在交流电感中先出现电动势（Electromotive force，E），然后是电感（L），最后是电流（I）。换句话说，在电感器中电压始终“在前”，电流“在后”，E、L、I 正好对应“ELI”，无论电压的初始相角如何，该表达式对纯电感电路始终成立。

频率对感抗的影响

The Effect of Frequency on Inductive Reactance

当将 50 Hz 电源连接到合适的交流电感上时，如前所述，电流会滞后 90°，并在每个半周期结束（电压反向）之前达到峰值 I 安培。也就是说，电流在 T 秒内上升到其最大值。

如果我们改为对线圈施加相同峰值电压的 100 Hz 电源，电流仍然滞后 90°，但其峰值会低于 50 Hz 时的值，因为频率升高后，可用于达到峰值的时间缩短为 \frac{1}{2}T秒。同时，线圈内磁通的变化速率也因频率增加而加快。

由上述感抗公式可知，无论是频率还是电感量增加，线圈的整体感抗值都会相应增大。

• 当频率增大并趋于无穷大时，电感的感抗（即其阻抗）也会趋于无穷大，表现为开路；

• 反之，当频率趋于零或直流时，感抗会降低至零，表现为短路。

这表明感抗“与频率成正比”，在低频时数值很小，而在高频时数值很大，如下图所示。

感抗随频率变化

Inductive Reactance against Frequency

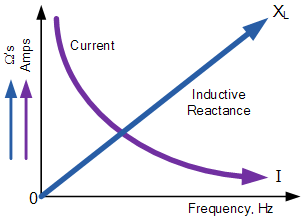
电感器的感抗随着其两端频率的增加而增大，因此感抗与频率成正比（ X_L \propto f），因为电感器产生的反电动势等于电感量乘以电流变化率。

同时，随着频率的增加，流过电感器的电流值也会减小。

我们可以将纯交流电感在极低频和极高频条件下的感抗变化表示如下：

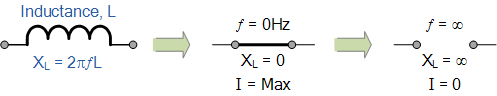
纯电抗交流电路可以用以下公式表示:

那么，我们是如何得到这个公式的呢？实际上，电感器中的自感电动势由法拉第定律决定，该定律产生了“自感”效应。当电流通过电感线圈时，交流电流的变化率会在同一线圈中感应出一个电动势，用以抵抗电流的变化。在线圈中，这种由流过线圈的电流所产生的磁场抵抗任何电流变化的效应称为“自感”self-inductance。

此自感电动势的最大电压值对应于电流变化率的最大值，该线圈两端的电压值可表示为：

或者写成

其中： \dfrac{d}{dt} 表示电流关于时间的变化率。

流经电感线圈 L 并在其周围产生磁通的正弦电流可表示为：

将上述正弦电流表达式代入自感电压公式，可得：

对正弦电流进行微分可得：

余弦恒等式

表明余弦波实际上就是相位提前 90^\circ 的正弦波。因此，我们可以将上述方程重写为正弦波形式，以定义交流电感两端的电压为：

其中：

• V_{\max} = \omega L I_{\max} = \sqrt{2}\,V_{\text{RMS}}，即最大电压幅值；

• \theta = +90^\circ 为电压与电流波形之间的相位差（相角）。这表明纯电感电路中，电流相对于电压滞后 90^\circ。

在相量域

In the Phasor Domain

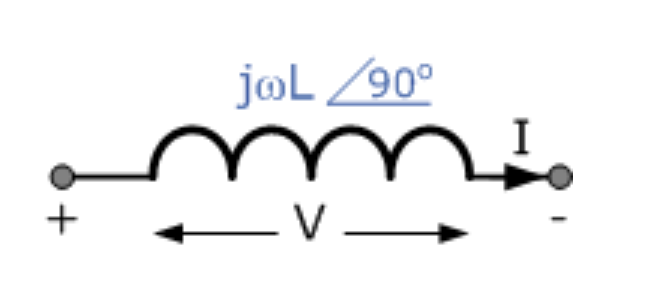
在相量域中，线圈两端的电压表示为：

其中：

而在极坐标形式中，可写作： X_L∠90°，其中：

串联 R＋L 电路中的交流

AC through a Series R + L Circuit

正如前面所示，通过纯电感线圈的电流比电压滞后 90°。这里所说的纯电感线圈是指没有欧姆电阻，因此也不存在 I^2R 损耗。但在现实中，不可能只有纯粹的交流电感。

所有电气线圈、继电器、螺线管和变压器的绕组都会存在一定的电阻（无论多小），因为铜线本身具有电阻率。因此，我们可以将电感线圈视为一个电阻 R 与一个电感 L 串联组成，这种情况可粗略称为“非纯电感”impure inductance。

如果线圈具有某种“内部”电阻，就需要将线圈的总阻抗表示为电阻与电感的串联。在同时包含电感 L 和电阻 R 的交流电路中，组合两端的电压 V 就是两部分电压 V_R 和 V_L 的相量和。

这意味着流过线圈的电流仍会滞后于电压，但滞后角小于 90°，具体取决于 V_R 和 V_L 的大小及其相量和。电压与电流波形之间的新相位角即它们的相位差，用希腊字母 \Phi 表示。

下图所示电路中，一个非电感性的纯电阻 R 与一个纯电感 L 串联。

串联电阻─电感电路

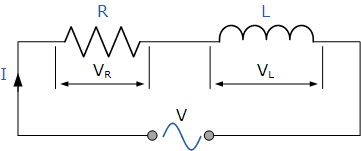
在上述 RL 串联电路中，我们可以看到电流在电阻和电感两端是相同的，而电压则由两部分电压 V_R 和 V_L 组成。这两部分电压的合成电压既可以通过数学计算求得，也可以通过绘制相量图来确定。

为了能够绘制相量图，必须先确定一个参考或公共量；在串联交流电路中，由于相同的电流流过电阻和电感，因此电流就是参考源。下图给出了纯电阻和纯电感各自的相量图：

两个纯元件的相量图

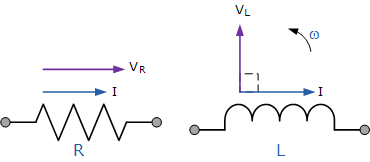
从上图及我们之前关于交流电阻的教程中可以看出，纯电阻电路中的电压和电流同相，因此电压向量 V_R 按同一比例与电流向量重叠绘制。

同样，如上所述，在纯交流电感电路中，电流相对于电压滞后，因此电感电压向量 V_L 按与 V_R 相同的比例绘制，并相对于电流向前 90^\circ，如图所示。

合成电压的相量图

Vector Diagram of the Resultant Voltage

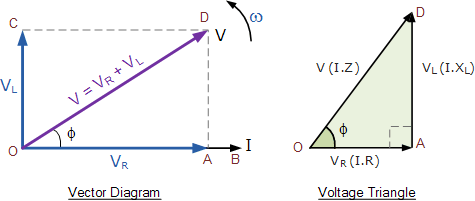
从上述相量图可以看出，OB 线是水平方向的电流参考线，OA 线是与电流同相的电阻分量电压。OC 线表示感性电压，它比电流超前 90°，因此仍然可以看出电流相对于纯电感电压滞后 90°。OD 线则表示合成后的电源电压。具体而言：

• V 为所加电压的有效值（r.m.s. 值）。

• I 为串联电路中电流的有效值。

• V_R 为电阻上的压降，等于 I\cdot R，与电流同相。

• V_L 为电感上的压降，等于 I\cdot X_L，比电流超前 90°。

由于在纯电感中电流恰好滞后电压 90°，由各自的压降 V_R 和 V_L 绘制出的合成相量图构成了一个直角电压三角形（如图 OAD 所示）。因此我们也可以应用勾股定理来计算串联电阻—电感（RL）电路的合成电压数值。

因为

所以，所加电压即为两者的向量和，表示为：

\sqrt{R^2 + X_L^2}的数量，RL 电路的阻抗量表示该电路的阻抗 Z。

交流电感的阻抗

阻抗 Z 是含有电阻（实部）和电抗（虚部）的交流电路中对电流流动的“总”阻碍，单位同样为欧姆（Ω）。阻抗取决于电路的角频率 \omega，因为频率会影响电路的电抗分量；在串联电路中，所有的电阻和电抗阻抗会相加。

阻抗也可表示为复数形式：

但它并不是一个相量，而是多个相量合成后的结果。如果将上述电压三角形的各边除以电流 I，即可得到一个新的三角形，其三边分别对应电路的电阻 R、电抗 X_L 和阻抗 Z，即下图所示

RL 阻抗三角形

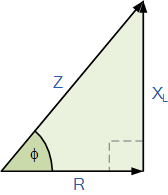
那么： (\text{阻抗})^2 = (\text{电阻})^2 + (j\,\text{电抗})^2，其中 j 表示 90^\circ 的相移。

这意味着电压与电流之间的正相位角 \theta 为：

相位角

相位角 φ 的计算公式如下：

其中：

• Z 为电路总阻抗；

• R 为电阻；

• X_L 为感抗；

• \varphi 为电压相量相对于电流相量的正相位差。

虽然上述示例表示一个简单的非纯交流电感，但如果将两个或多个电感线圈串联，或将单个线圈与多个非电感性电阻串联，则所有电阻元件的总电阻等于

从而得到电路的总电阻值。同样，所有电感元件的总电抗等于

从而得到电路的总电抗值。

这样，一个包含多个扼流圈、线圈和电阻器的电路，就可以简化为由单个电阻与单个电抗串联组成的阻抗值 Z，即

交流电感示例 1

在下图电路中，电源电压定义为： V(t) = 325\sin\bigl(314t - 30^\circ\bigr)，电感： L = 2.2\ \mathrm{H}。求：

1. 流过线圈的有效值电流；

2. 绘制相应的相量图。

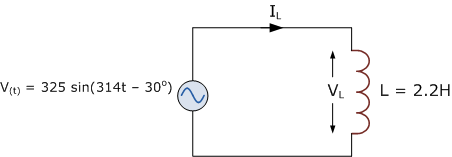
线圈两端的有效值电压与电源电压相同。如果电源峰值电压为 325 V，则对应的有效值为 230 V。将该时域值转换为极坐标形式可得：

线圈的感抗为：

然后，流过线圈的电流可用欧姆定律求得：

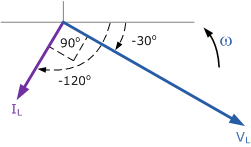
由于电流相对于电压滞后 90^\circ，其相量图将为：

交流电感示例 2

一个线圈的电阻为 30 Ω，电感为 0.5 H。如果流过线圈的电流为 4 A，电源频率为 50 Hz，求电源电压的有效值。

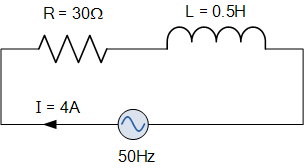
该电路的阻抗将为：

然后，各元件上的电压降计算如下：

电流与电源电压之间的相位角计算如下：

相位图如下:

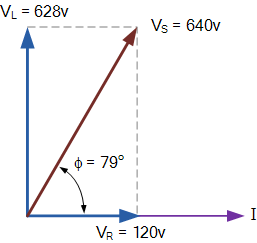
在下一个关于交流电容的教程中，我们将研究当稳态正弦交流波形施加到电容器上时的电压–电流关系，并展示纯电容器和非纯电容器的相量图表示。

附录

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途