直流串联电路
串联电路是将多个元件按一条线串联在一起,形成仅有一条电流路径,其各电压降之和等于所加电压。
什么是直流串联电路
What Is a DC Series Circuit
直流串联电路(或称“串联连接电路”)是将多个独立的电路元件,如电阻、电容和电感,端对端地连接在一起,仅提供一条电流路径。因此,直流串联电路通常定义为只有一个闭合回路或电流环路,而不像直流并联电路那样可存在多条电流路径。
在串联电路中,由于不存在分支节点或支路,电流无法分流或汇聚,我们可以正确地说,流经串联电路任意部分的电流大小 I 与流经其他部分的电流大小完全相同。也就是说,直流串联电路的所有部分具有相同的电流值。
电路由多种类型的元件和器件组成,串联电路亦如此。它们不仅限于电阻(R),还可包括以串联方式连接的其他电子元件,例如电感(L)和电容(C),以及 R、L、C 的各种组合。
因此,我们可以说,串联电路由电压源或电流源、导线(电线)以及各种元件(电阻、电容、电感等)构成,这些元件以一定方式连接,使电流能够绕单一回路或路径流动,串联元件的组合通常称为“串联支路”。
电压源(如电池)在电路中建立电势差,迫使电流流动。考虑下图所示的直流串联电路:
直流串联电路图示
DC Series Circuit
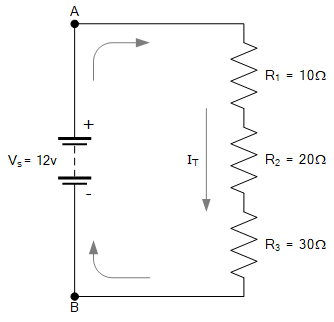
在上面简单的串联电路中,由 12 V 电池源看到的等效电阻 R_T 等于各个电阻值之和,即:
为了简便,我们在本例中使用电阻来说明直流电路。但同样的规则也适用于交流电路,此时应计算各元件的串联总阻抗。
注意:串联电路的等效电阻 R_T 始终大于电路中任何单个电阻的最大值。如果有 n 个电阻(或阻抗)串联,则
R_T = R_1 + R_2 + \cdots + R_n
由于串联电路中只有一条闭合回路,电源(V_S)提供的总电流 I_T 在每个电阻中都相同。由欧姆定律
可得该电路中的电流为:
欧姆定律还指出,任何电压都可表示为电流与电阻的乘积:
因此,我们可以计算出各电阻上的电压降:
各电压降之和等于电池电压:
在直流电路中,“和”即线性相加;若是交流阻抗,则应按矢量和方式相加。
电压分配
Voltage Division
当电源电压 V_S 加在多个串联电阻上时,每个电阻上的电压与该电阻值成正比。对于总电阻为 R_T、供电电压为 V_S 的任意串联电阻网络,某一电阻 R_X 上的电压降为:
电压分配定理的优点在于,我们仅凭电源电压和总串联电阻便可求得各串联电阻元件上的电压降,而无需知道回路电流 I。由此可快速计算电路中任意电阻 R_n 的电压。
因此,我们使用电压分配定理来确定上图中三只电阻的电压降:
由此可见:V_{R1}=2\ \mathrm{V}、V_{R2}=4\ \mathrm{V}、V_{R3}=6\ \mathrm{V},与前述基于欧姆定律和回路电流的计算结果完全一致。
注意,尽管此处示例为三只串联电阻,电压分配定理对任意多个串联电阻均适用;所用电压 V_S 亦不必限于电池电压,可为任一串联组合两端的总电压。
最后一点要注意的是,这些电压降与电压源(或电压升)同样可用基尔霍夫电压定律(KVL)来总结。
基尔霍夫电压定律(KVL)
基尔霍夫电压定律指出:闭合回路中所有电压的代数和必须等于零,即电压源之和等于电压降之和。但在应用时须考虑各电压源与电压降的符号——电压源可被视为负向电压降,电压降亦可被视为负向电压源。
对于本例串联电路,我们已知各电阻上的电压降之和等于电池电压:
因此
验证了本例电路满足基尔霍夫电压定律。
串联电路示例 2 五个阻值分别为 5 Ω、 12 Ω、 20 Ω、 15 Ω 和 8 Ω 的电阻串联,并将该串联组合并接于 24 V 的直流电池电压源两端。利用电压分配定理,计算回路电流 I_S 及各电阻上的电压降。
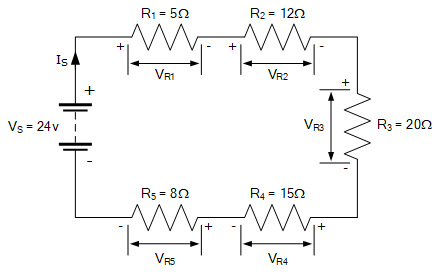
求总串联电阻 R_T
R_T = R_1 + R_2 + R_3 + R_4 + R_5 \\ = 5\Omega + 12\Omega + 20\Omega + 15\Omega + 8\Omega \\ = 60\Omega求回路电流 I_S
I_S = \frac{V_S}{R_T} = \frac{24}{60} = 0.4\ \mathrm{A}求各电阻上的电压降(电压分配定理) 电压分配公式:
V_{R_n} \;=\; V_S\,\frac{R_n}{R_T}代入可得:
\begin{aligned} V_{R1} &= 24 \times \frac{5}{60} = 2.0\ \mathrm{V},\\ V_{R2} &= 24 \times \frac{12}{60} = 4.8\ \mathrm{V},\\ V_{R3} &= 24 \times \frac{20}{60} = 8.0\ \mathrm{V},\\ V_{R4} &= 24 \times \frac{15}{60} = 6.0\ \mathrm{V},\\ V_{R5} &= 24 \times \frac{8}{60} = 3.2\ \mathrm{V}. \end{aligned}欧姆定律校验 也可用 V=I\times R 并结合回路电流进行校验:
\begin{aligned} V_{R1} &= 0.4 \times 5 = 2.0\ \mathrm{V},\\ V_{R2} &= 0.4 \times 12 = 4.8\ \mathrm{V},\\ V_{R3} &= 0.4 \times 20 = 8.0\ \mathrm{V},\\ V_{R4} &= 0.4 \times 15 = 6.0\ \mathrm{V},\\ V_{R5} &= 0.4 \times 8 = 3.2\ \mathrm{V}. \end{aligned}因此:
2.0 + 4.8 + 8.0 + 6.0 + 3.2 = 24\ \mathrm{V},
与电源电压相符。
教程摘要
总结如下:直流串联电路(DC Series Circuit),或称串联连接电路,是将两个或多个电路元件端对端相连,形成一个闭合回路,这些串联元件的组合通常称为“串联支路”(string)。
由于电流无法在串联回路的任一点离开或进入,流经该回路的电流在电路各处均相同,因为只有一条路径可循。注意,在直流串联电路中,元件的连接顺序对电流路径没有影响。
然而,串联电路的一个主要缺点是:如果串联支路中的任一元件发生故障或断开(即开路),整个电路将被中断,电流停止流动——串联电路对每个元件均有依赖性。
我们可将串联电路的主要特性总结为:
回路电流:由于仅有一条闭合路径,串联电路中所有元件上的电流相同。
总电阻:直流串联电路的等效电阻
R_T = \sum_{n} R_n等于各元件电阻之和。
电压分布:直流串联电路中总电压降为各元件电压降的线性相加;若为交流电路,则需按矢量相加。
同时,电压降可以通过欧姆定律
或电压分配定理来求得;基尔霍夫电压定律(KVL)则说明,串联电路中所有电压降之和等于所加电源电压。
此外,各元件上的电压降与其电阻成正比,且这些电压降之和必等于所加电压。
附录
单词表
声明
本文仅供学习,禁止用于任何的商业用途。

