叠加定理
Superposition Theorem
叠加定理可用于确定线路元件上的电压和/或电流,仅考虑单一电源的作用。 叠加定理是我们用来分析线性电路中电压和电流的另一种工具。如果电路包含一个或多个独立的电压源和/或电流源,我们可以使用叠加定理来找出每个独立电源单独作用时对电路中各处电压和/或电流的贡献,然后将它们代数相加,得到电路中任意一点的实际电压和/或电流值。
也就是说,我们可以利用叠加定理,将由于每个独立电源单独作用所产生的电压和电流在电路中“叠加”或代数相加,从而得到特定元件或节点上的总电压或总电流。
使用叠加定理的优势在于,相对于网孔分析或节点分析,不需要使用行列式、联立方程或矩阵代数来分析给定的电路,数学运算更为简便。叠加定理在分析既包含直流电路又包含交流电路、可能含有多个电源的情况时尤其有用。
然而,叠加定理的劣势在于它仅适用于线性电路。幸运的是,对于无源元件——电阻(R)、电感(L)和电容(C)——它们的电压-电流关系都是线性的。
与之前的电路分析技术(基尔霍夫定律、戴维南定理、诺顿定理等)类似,我们必须“关断”电路中的所有电源,仅保留一个理想电压源或一个理想电流源进行分析。关断操作很简单:将所有电流源开路(open-circuit),将所有电压源短路(short-circuit),以便求出某一电压源或电流源对电路的单独影响。
也就是说,用短路替换电压源,因为短路两端电压降为零,即
而用开路替换电流源,因为开路中没有电流流动,即
(这里假设电源皆为理想电源)。
注意,受控源(dependent sources)并不具有固定的电压或电流值,它们的值由电路中其它的电压或电流或外部信号控制,因此不能“关断”或“失活”。
叠加定理示例1
下面,我们先考虑前面教程中提到的“T 型”直流电路。
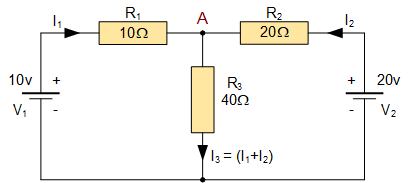
在这里,我们需要求出流过中央 40\ \Omega 电阻 R_3 的电流,也就是 I_3。在电路分析过程中,无论是顺时针还是逆时针方向进行分析,都不会影响最终结果,只要我们在整个分析过程中保持方向的一致性即可。接下来,我们首先将 20\ \mathrm{V} 电池等效为短路,这样就只剩下 10\ \mathrm{V} 电池单独作用于电路,如下图所示。
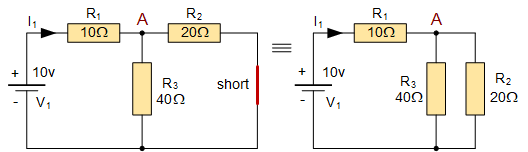
可以看出,将电压源 V_2 对地短路后,右侧的 20\,\Omega 电阻实际上与中央的 40\,\Omega 电阻等效地并联。作为两个并联连接的电阻,它们的等效并联电阻计算为:
左侧的 10\,\Omega 电阻 R_1 与等效并联电阻 R_{\mathrm{eq}1}=13.33\,\Omega 串联,形成总串联电阻
电流 I_1 经此电阻流过。
应用分压定律,可求出节点 A 处相对于 10\,\mathrm{V} 电源 V_1 的电压:
求电流 I_{R3(1)} 由 10\,\mathrm{V} 电源 V_1 驱动,通过 40\,\Omega 电阻 R_3 的电流为:
因此,当仅保留 V_1 时,流经 R_3 的电流为 143\,\mathrm{mA}。
为了验证,可利用节点 A 上的两个并联支路(40\,\Omega 与 20\,\Omega):
则
结果一致。
求电流 I_{R3(2)} 采用相同方法和思路,下面计算由 20\,\mathrm{V} 电源 V_2 驱动时,流过电阻 R_3 的电流。
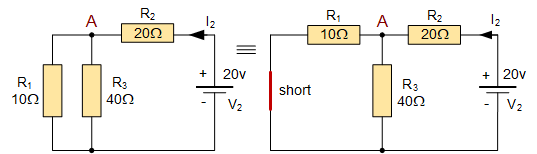
将 10\,\mathrm{V} 电池 V_1 等效为短路,仅保留 20\,\mathrm{V} 电池 V_2 单独作用于电路。此时, R_1 与 R_3 构成两条并联支路,其等效并联电阻为
右侧的 20\,\Omega 电阻 R_2 与该等效并联电阻串联,总串联电阻
形成电流 I_2 的回路。
同样应用分压定律,可求出仅由 V_2 作用时节点 A 处的电压:
巧合的是,无论哪一路电源单独作用时,节点 A 处的电压均为 5.71\,\mathrm{V}。由 V_2 驱动的 R_3 上电流为:
要得到 I_{R3} 的总值及方向,只需将两次计算得到的电流代数相加:
该值与前面使用基尔霍夫定律、戴维南定理和诺顿定理计算所得的 0.286\,\mathrm{A} 相同。
当将两路电源重新接入电路后,用欧姆定律可计算节点 A 处电压,从而得到 R_3 上的电压降:
同样与前述教程结果一致。
由此可见,叠加定理能简化含有两路或多路电压/电流源的线性网络分析所需的运算,也可用于含直流和交流电源的网络。
注意:叠加定理不适用于功率计算,因为功率与电流的平方(I^2R)及电压的平方(V^2/R)成正比,属于非线性量。
叠加定理示例2
现在我们在下图电路中引入一个电流源,并利用叠加定理求解2 Ω电阻 R1 上的电压降。
叠加定理电路图
Superposition Circuit
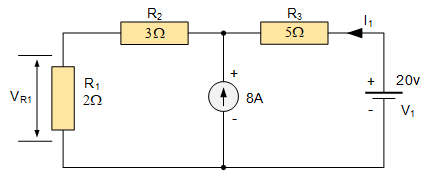
再次要分析该电路时,我们必须将电压源短路,将电流源开路,以确保任何时刻电路中只有一个电动势源在供电。首先,我们将把 8 A 电流源开路,仅用 20 V 电压源来分析电路,如下所示。
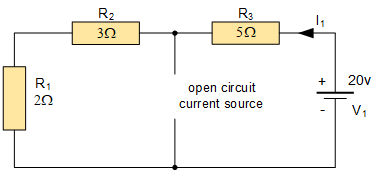
显然,此时电路等同于一个串联电阻电路,连接在 20 V 电源两端。根据基尔霍夫电压定律(KVL):
又由欧姆定律可得电流
因此,流过该串联电路的电流为 2 A,电阻 R₁ 上的电压降为:
也就是说,由 20 V 电池引起的 R₁ 上电压降为 4 V。如果需要,还可以用分压公式继续求其余电阻上的电压降。
现在将电压源 V₁短路,并重新接入 8 A 电流源,电路则变为:
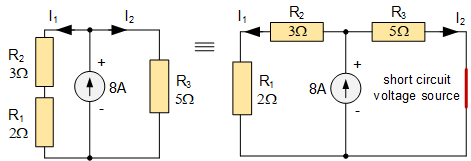
我们现在可以看到,电路已变为一个并联电阻电路,连接在 8 A 电流源两端,常称为电流分配电路。电流源为两条并联支路提供电流:一条支路上有 R₁ 和 R₂ 串联,另一条支路上只有 R₃。
根据基尔霍夫电流定律(KCL),总电流等于所有并联支路电流之和,即
由于我们关注的是 R₁ 支路上的电压降,需要先求流过 R₁∥R₂ 支路的电流 I₁。
电流分配定理指出,某一支路电流等于总电流乘以该支路等效电阻与所有支路等效电阻之和的比值。于是流过 R₁+R₂ 串联支路的电流为:
因为 R₁∥R₂ 支路中有 4 A 流过,我们再用欧姆定律算出 R₁ 上的电压降:
注意,如果各并联支路的电阻相等,电流会均分;如果电阻不同,电流会更多地流向电阻较小的那一路。
因此,当 8 A 电流源和 20 V 电压源同时作用时,R₁ 上的总电压降为两部分之和:
同样的方法还可用于求 R₂、R₃ 上的电压降。
叠加定理总结
在任何含有多个独立电压源或电流源的线性电路中,我们可以使用叠加定理来求出各电路元件在每个独立源单独作用时所产生的电压和/或电流,然后将它们的影响叠加起来得到整个电路的总响应。
为了使叠加定理正确适用,需要将所有理想电压源替换为短路,将所有理想电流源替换为开路。注意,非理想源一般用其内阻来代替。
使用叠加定理分析电路的基本步骤如下:
确定电路中的所有独立源,例如电压源和电流源,并在分析中每次只选定其中一个源。
将其他所有独立源关闭(电压源短路,电流源开路),仅用一个源分析电路。
利用标准的电路分析方法(欧姆定律、基尔霍夫定律)求出所选单一源作用下所需电路元件、支路或节点的电压或电流。
对电路中的每个独立源重复上述过程,每次仅考虑该源的影响,而保持其它源关闭。
将各次分析得到的响应按代数规则相加,以得出目标电路元件、支路或节点的总响应。
当所有源同时作用时,注意响应的极性、符号约定和电流方向。
注意,叠加定理仅适用于线性电路;当独立源较多时,分析过程会过于繁琐,此时节点分析或网孔分析等方法可能更为实用和高效。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

