电能与功率
电能为在电路中产生工作或动作所需的功率提供能量,其单位为焦耳每秒(\mathrm{J/s})。
电能是电路通过产生动作而做功的能力。该动作可以有多种形式,例如热能、电磁能、机械能、电能等。电能既可以由电池、发电机、直流发电机和光伏装置等产生,也可以通过燃料电池、电池、电容器或磁场等存储以备将来使用。因此,电能既可以被产生,也可以被存储。
我们还记得在中学科学课上,能量守恒定律The Law of the Conservation of Energy指出能量既不能被创造也不能被毁灭,只能转换。但为了使能量做任何有用的功,就必须将其从一种形式转换为另一种形式。例如,电动机将电能转换为机械能或动能(旋转能),而发电机则将动能转换回电能以为电路提供动力。
也就是说,电气机械通过做功将能量从一种形式转换为另一种形式。另一个例子是灯、灯泡或 LED(发光二极管),它们将电能转换为光能和热(热能)。因此,电能非常多功能,可轻松转换为多种不同形式的能量。
为了使电能移动电子并在电路中产生电流,必须做功,也就是说,电子必须在导线或导体中移动一定距离。所做的功作为能量储存在电子的流动中。因此,“功”就是我们给予这一能量过程的名称。
因此,我们可以说功和能量实际上是相同的,因为能量可以定义为“做功的能力”。注意,所做的功或传递的能量对于机械系统、热系统和电系统同样适用,这是因为机械能、热能和电能可以相互转换。
电能:电压
Electrical Energy: The Volt
如我们所知,能量是做功的能力,其标准单位为焦耳(\mathrm{J})。1 焦耳的能量定义为电流 1\mathrm{A} 在电压 1\mathrm{V} 下移动 1\mathrm{s} 所消耗的能量,即
电流是电荷(电子)在电路中移动形成的,但是要将电荷从一个节点移动到另一个节点,就需要一种力来做功移动电荷,这种力就是电压。
我们通常认为电压(\mathrm{V})存在于电路或电池供电的两个不同端子、点或节点之间。但电压很重要,因为它提供了将电荷从一点移动到另一点所需的功,无论是正方向还是反方向。
电压或由电压源在两个端子或节点之间提供的电势差被定义为 1 伏(\mathrm{V}),当在这两个端子之间移动 1 库仑(\mathrm{C})的电荷时所使用的能量为 1 焦耳(\mathrm{J})。
换句话说,两点或两个端子之间的电压差是将 1 库仑电荷从 A 移动到 B 所需的功(以焦耳为单位)。因此,电压可以表示为:
电压单位
The Voltage Unit
其中:voltage 为电压(单位: \mathrm{V} ), 焦耳为功或能量(单位: \mathrm{J}),库伦为电荷量(单位: \mathrm{C})。因此,当 \mathrm{J}=1\mathrm{J}、\mathrm{C}=1\mathrm{C} 时, V=1\mathrm{V}。
电能示例 No.1
某电池在电路中移动 15\mathrm{C} 电荷时消耗 135\mathrm{J} 能量,求该电池的端电压。
由上式可得,每一库仑电荷具有的能量为
即在此示例中,每一库仑电荷具有 9\mathrm{J} 的能量。
电能·安培
Electrical Energy: The Ampere 我们已经知道,电荷的单位是库仑(Coulomb),电荷在电路中流动时就形成了电流。但由于库仑的符号也是大写字母 “C”,容易与电容(Capacitance)的符号 “C” 混淆。
为避免这种混淆,通常用大写字母 “Q” 或小写字母 “q” 来表示电荷,即 quantity(数量)的首字母。因此:
注意,电荷 Q 可以为正电荷(+Q)或负电荷(-Q),分别表示电子或空穴hole的过量。
电子形式的电荷在闭合电路中的流动称为电流。但“流动”意味着电荷必须移动,那么是什么推动电荷移动?答案是电压。
两个点之间的电压(或电势差)提供了使电荷以电流形式在电路中移动所需的电能。因此,移动电荷所做的功由电势差提供;若两点间无电势差,则无电荷移动,也就无电流流动。静止不动的电荷称为静电。
如果说电荷的移动形成电流,那么我们可以将电流定义为电荷移动的速率。选取电路中任一点,测量恰好在一秒钟内通过该点的电荷量,就可以得到该点的电流强度,单位为安培(Ampere,A)。
因此,1 安培的电流即是 1 库仑的电荷在 1 秒钟内通过某点:
安培单位
The Ampere Unit
在此处:Q 是电荷量(单位:库仑),t 是电荷移动所用的时间间隔(单位:秒)。换句话说,电流不仅具有大小(通过的电荷量),还具有特定的方向。
通常用大写字母 “I” 或小写 “i” 表示电流,皆表示强度(intensity),即产生电子流动的电荷浓度。对于恒定的直流电流,一般使用大写 “I”;而对于随时间变化的交流电流,则常用小写 “i”,其中i(t)表示时刻 t 的瞬时电流值。
有时可以通过下面的三角形来帮助记忆三者关系:
安培三角形
The Ampere Current Triangle
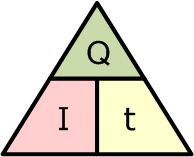
将上述标准公式进行变换,可得到以下等价的几种形式:
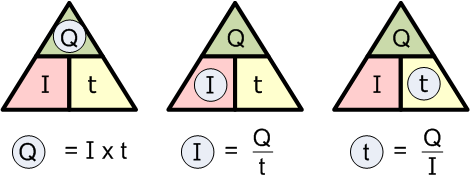
电能示例 No.2
已知:电荷量 Q=900 库仑,时间 t=3 分钟 首先将分钟换算为秒:
t = 3\ \text{min} = 3 \times 60\ \mathrm{s} = 180\ \mathrm{s}电流为
I = \frac{Q}{t} = \frac{900\ \mathrm{C}}{180\ \mathrm{s}} = 5\ \mathrm{A}已知:电流 I=3 安培,时间 t=90 秒 电荷量为
Q = I \times t = 3\ \mathrm{A} \times 90\ \mathrm{s} = 270\ \mathrm{C}
电能·瓦特
Electrical Energy: The Watt
电功率(Electrical Power)是电压与电流的乘积,如欧姆定律所定义。电流可看作能量消耗做功的速率。我们前面已经说过,电压提供了将 1 库仑电荷从 A 点移动到 B 点所需的能量(以焦耳为单位),而电流则是电荷移动的速率(单位时间内的电荷量)。那么,这两种定义如何联系起来呢?
若电压 V 等于焦耳每库仑(V = \tfrac{J}{C}),电流 I 等于库仑每秒(I = \tfrac{Q}{t}),则电功率 P 可以定义为二者的乘积:
the Watt
由上述推导可知,电功率也等于每秒所做的功,即每秒消耗的焦耳数。因此,电功率的单位瓦特(Watt,W)必须等同于焦耳每秒(J/s)。
电功率公式
Electrical Power Formula
因此,若
则可推出:
即功等于功率乘以时间,
因此,电能(所做的功)可由功率乘以电流流过时间(秒)来计算。
由此可见,电能的单位取决于功率和时间所用的单位。如果以千瓦(\mathrm{kW})为功率单位、以小时(\mathrm{h})为时间单位,则耗电量为
通常简写为千瓦时(\mathrm{kWh})。
电能示例 No.3
一个100\mathrm{W}的灯泡仅点亮 1\mathrm{h}。该灯泡消耗了多少焦耳 \mathrm{J}的电能?
注意:使用焦耳(J)表示电能时,常以千焦(kJ)为单位,故
由于焦耳数量较小,实用单位还有
此外,1 个电度(1,kWh)等于
同样,瓦特(W)是电功率的单位,常用千瓦(kW)和兆瓦(MW)表示:
因此,千瓦(或兆瓦)是电功率单位,而千瓦时(kWh)是电能单位。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

