电流分流器
Current Divider
电流分流电路具有两个或多个并联支路供电流流动,但并联电路中所有元件的电压相同。
电流分流器
电流分流器是一个并联电路,其中源电流或供电电流在多个并联连接的路径(称为支路)之间分配。在并联电路中,所有元件的端子彼此相连,共享相同的两个端节点。这导致电流可沿不同路径和支路流动。然而,不同元件中的电流值可以不同。
并联电路的主要特性是,尽管它们可能产生不同的支路电流,但所有连接路径的电压都是相同的。即
因此,无需求解各个电阻的电压,可通过基尔霍夫电流定律(KCL)及欧姆定律轻松求出支路电流。
电流分流定理
Current Divider Rule
最简单易懂且最基本的无源电流分流网络是两个电阻并联的情况。电流分流定理允许我们将总电流按比例计算流经每个并联电阻支路的电流。
那么 “什么是电流分流定理”,以及如何将其用于并联电路?请考虑下图所示的电阻网络。
电流分流电路
Current Divider Circuit
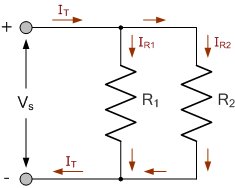
此基本电流分流电路由两个并联电阻 R_1 和 R_2 组成。该并联组合将源电流 I_S 分成两路电流 I_{R1} 和 I_{R2},然后再汇合返回到电源。
由于源电流等于各支路电流之和,根据基尔霍夫电流定律 (KCL),电路中的总电流 I_T 为:
又因为并联电路中各元件两端电压相同,记为 V,并根据欧姆定律 V = I \, R,可得:
将上述式子代入 I_T:
解出并联组合两端电压 V:
将 V 代入各支路电流表达式,并化简得:
注意,上述各支路电流公式的分子中出现的是“对偶”电阻:求 I_{R1} 时分子用 R_2,求 I_{R2} 时分子用 R_1。这是因为每一路电流与其对应电阻成反比,电阻越小,电流越大。
电流分流示例 1
一只 20\ \Omega 电阻与一只 60\ \Omega 电阻并联,若该并联组合接在 30\ \mathrm{V} 电池两端,求各电阻的电流以及电源总电流。
支路电流计算:
总电流:
还要记住,并联电阻的等效电阻 R_{\mathrm{eq}} 总是小于并联中最小电阻的欧姆值,且随着并联电阻数量的增加,等效电阻会减小。
有时如果已知电源电流或总电流 I_T,则无需计算所有支路电流。此时,可根据基尔霍夫电流定律,将已知支路电流从总电流中相减,即可求得剩余支路电流。
电流分流示例 2
三个电阻按照下图所示连接,形成一个电流分流电路。如果电路由 100\ \mathrm{V} 电源驱动,且电源容量为 1.5\ \mathrm{kW},请运用电流分流定理计算各支路电流,并求出等效电路电阻。
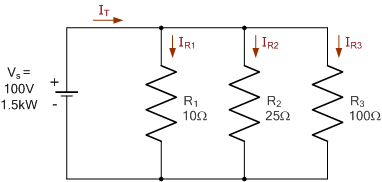
总电路电流 I_T:
I_T = \frac{P}{V} = \frac{1500}{100} = 15\ \mathrm{A}.等效电阻 R_{EQ}:
R_{EQ} =\Bigl(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\Bigr)^{-1} =\Bigl(\frac{1}{10}+\frac{1}{25}+\frac{1}{100}\Bigr)^{-1} =\frac{1}{0.15}=6.667\ \Omega.各支路电流 I_{R1},\,I_{R2},\,I_{R3}:
I_{R1} =I_T\frac{R_{EQ}}{R_1} =15\times\frac{6.667}{10} =10\ \mathrm{A},I_{R2} =I_T\frac{R_{EQ}}{R_2} =15\times\frac{6.667}{25} =4\ \mathrm{A},I_{R3} =I_T\frac{R_{EQ}}{R_3} =15\times\frac{6.667}{100} =1\ \mathrm{A}.我们可以通过基尔霍夫电流定律检验计算结果,因为所有支路电流之和等于总电流,因此:
I_T = I_{R1} + I_{R2} + I_{R3} = 10 + 4 + 1 = 15\ \mathrm{A},如预期所示。因此,总电流 I_T 按照由各支路电阻决定的简单比率进行分配。
此外,随着并联电阻数量的增加,在给定电源电压 V_S 的情况下,源电流 I_T 也会增大,因为并联支路增多,可分担的电流路径增加。
使用导纳法进行电流分流
Current Division using Conductance’s
另一种求解直流并联电路中各支路电流的简单方法是使用导纳法。在直流电路中,导纳是电阻的倒数,记作 “G”。
由于导纳 G 是电阻 R 的倒数,而电阻的单位为欧姆(\Omega),其倒数称为“摩”(℧,倒置的欧姆符号)。因此
导纳的国际单位为西门子(Siemen,符号 \mathrm{S})。
对于并联连接的电阻,其等效或总导纳 C_T 等于各支路导纳之和,如下所示。
电流分流器的并联导纳图示
Parallel Conductance of a Current Divider
因此,如果一个电阻的固定值为 10\,\Omega,其等效导纳为 0.1\,\mathrm{S},以此类推。由于导纳与电阻互为倒数,导纳值越大表示电阻值越小,反之亦然。我们还可以使用前缀来表示导纳:毫西门子(\mathrm{mS})、微西门子( \mu\mathrm{S})乃至纳西门子( \mathrm{nS})用于表示非常小的导纳。因此,一个 10\,\mathrm{k}\Omega 的电阻将具有 100\,\mu\mathrm{S} 的导纳。
使用欧姆定律中电流的表达式 I = \dfrac{V}{R},我们可以用导纳来定义支路电流:
事实上,我们可以更进一步地说,上述并联电阻网络的供给电流为:
但我们从上面知道,对于并联电路,电压对所有元件是相同的,且由于电压等于电流乘以电阻,
因此当使用导纳时,可以得出电压等于电流除以导纳,即
然后,我们可以将上述电流分流定理的公式用导纳 (G) 来表示,而不是电阻 (R),如下所示:
使用导纳的电流分流定理
Current Divider Rule using Conductance
因此
并联电阻 R_2 和 R_3 上的电流类似地表示为:
你可能已经注意到,与上述用电阻表示的公式不同,这里每个支路电流的分子均为对应支路的导纳:计算 I_{R1} 时使用 G_1,计算 I_{R2} 时使用 G_2。这是因为导纳正好是电阻的倒数。
电流分流示例 3
使用导纳法,求下图并联电阻电路中各支路电流 I_1、I_2 和 I_3。
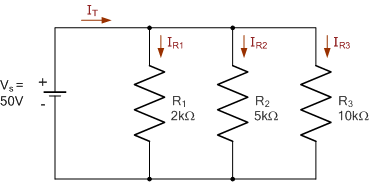
总导纳 G_T 为
因此
总电源电流 I_T 为
各支路导纳
各支路电流
由于导纳是电阻的倒数,上述电路的等效电阻为
明显小于最小支路电阻 R_1 = 2\,\mathrm{k}\Omega 。
电流分流定理总结
电流分流(Current Divider)或电流分配是指在并联电路中求取各支路电流的过程,此时每个并联元件上的电压相同。基尔霍夫电流定律(KCL)指出:流入某一节点的各支路电流代数和等于流出该节点的电流代数和,即代数和为零。
当已知等效电阻 R_{\mathrm{EQ}} 和总电流 I_T 时,也可利用基尔霍夫电流分流定理求得各支路电流。若仅有两条电阻支路并联,则某支路电流为总电流 I_T 的一部分;当两支路电阻相等时,电流平等分配。
当并联支路数目大于等于三时,先计算等效电阻:
再将总电流 I_T 按各支路电阻倒数之比分配给各支路,使电阻越小的支路所分得电流越大。此时
因此电流分流器常用于电流源驱动的场合。
在并联电路中使用导纳法(Conductance)同样方便,可简化数学运算。并联电路的总导纳等于各支路导纳之和:
其中导纳定义为电阻的倒数:
单位为西门子(Siemens,符号 S)。导纳方法既适用于直流(DC)电路,也适用于交流(AC)电路的电流分流分析。
附录
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

