电压分压器

Voltage Divider

电压分压电路用于从一个公共电压源产生不同的电压等级，但在串联电路中，各元件中的电流均相同。

电压分压器

The Voltage Divider

电压分压器（Voltage Divider）可将电压源分割成不同的电压等级。该电压源可以是相对于某一公共地或节点（通常为 0\mathrm{V}）的单一正电压或负电压源，例如 +5,\mathrm{V}、 +12,\mathrm{V}、-5,\mathrm{V} 或 -12,\mathrm{V} 等。也可以在双电源供电下建立分压网络，例如 \pm5,\mathrm{V} 或 \pm12,\mathrm{V} 等。但究竟什么是电压分压电路？电压分压器如何工作？

电压分压器也称为势垒分压器（potential divider），因为“Volt”（伏特）这个单位表示两点之间的电位差。势垒分压器是一种简单的无源电路，它利用串联连接元件上的电压降来产生源电压的固定分数值。

电位器（potentiometer）是最基础的电压分压实例。它是带有滑动触点的可变电阻器，我们可以在其两端加上电压，并根据滑动触点的位置获取相应比例的输出电压。但我们也可以使用单个电阻、电容或电感元件来构建分压器，因为它们都是双端元件，可串联连接。

电压分压法则

Voltage Divider Rule

最简单易懂的无源电压分压网络是将两个电阻串联连接。利用电压分压法则（Voltage Divider Rule），我们可以计算出每个串联电阻上的电压降。

电压分压电路

Voltage Divider Circuit

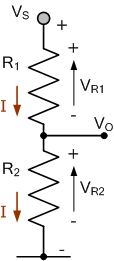
在此电路中，由两个电阻串联组成： R_1 和 R_2。由于两电阻串联连接，因此相同数值的电流必须流经电路中的每个电阻元件，因而在每个电阻元件两端产生了 I\times R 的电压降。

在该串联组合上施加电源电压 V_S 后，我们可以运用基尔霍夫电压定律（KVL）以及欧姆定律，以流经它们的公共电流 I 来求解各电阻两端的电压降。

解算流经该串联网络的电流 I 可得：

V_{S} = V_{R1} + V_{R2} \quad(\text{KVL})

V_{R1} = I \times R_{1},\quad V_{R2} = I \times R_{2}

\therefore V_{S} = I\,R_{1} + I\,R_{2} = I\,(R_{1} + R_{2})

\therefore I = \frac{V_{S}}{R_{1} + R_{2}}

根据欧姆定律，流经串联网络的电流可以简单地表示为：

I = \frac{V}{R}

由于该电流对两个电阻相同（ I\,R_1 = I\,R_2），我们可以计算上述串联电路中电阻 R_2 上的电压降为：

电压分压公式

Voltage Divider Formula

I_{R_{2}} = \frac{V_{R_{2}}}{R_{2}} = \frac{V_{S}}{R_{1} + R_{2}} \quad\therefore\quad V_{R_{2}} = V_{S}\,\frac{R_{2}}{R_{1} + R_{2}}.

同样地，对于电阻 R_{1}，可得：

I_{R_{1}} = \frac{V_{R_{1}}}{R_{1}} = \frac{V_{S}}{R_{1} + R_{2}} \quad\therefore\quad V_{R_{1}} = V_{S}\,\frac{R_{1}}{R_{1} + R_{2}}.

电压分压示例1

当一个 20\,\Omega 电阻与一个 40\,\Omega 电阻串联，并在该串联组合两端施加 12\,\mathrm{V} 直流电源时，流过电路的电流是多少？并计算各电阻上的电压降。

R_{T} = R_{1} + R_{2} = 20 + 40 = 60\ \mathrm{\Omega} \\ I = \frac{V_{S}}{R_{T}} = \frac{12}{60} = 0.2\ \mathrm{A}\quad\text{或}\quad200\ \mathrm{mA} \\ V_{R_{1}} = I \times R_{1} = V_{S}\,\frac{R_{1}}{R_{1}+R_{2}} = 12\left(\frac{20}{20+40}\right) = 4\ \mathrm{V} \\ V_{R_{2}} = I \times R_{2} = V_{S}\,\frac{R_{2}}{R_{1}+R_{2}} = 12\left(\frac{40}{20+40}\right) = 8\ \mathrm{V}

每个电阻都会产生一个 I \times R 的电压降，其大小与该电阻的阻值成正比。根据电压分压比法则（Voltage Divider Ratio Rule），我们可以看到阻值最大的电阻产生的 I \times R 电压降最大。因此， R_1 上的电压降为 4\,\mathrm{V}， R_2 上的电压降为 8\,\mathrm{V}。应用基尔霍夫电压定律（KVL）可验证，环路中各电压降之和恰好等于电源电压，即

4\,\mathrm{V} + 8\,\mathrm{V} = 12\,\mathrm{V}.

注意，如果使用两个相等的电阻，即 R_1 = R_2，那么串联后每个电阻上的电压降将各自恰好为电源电压的一半，因为分压比为 50%。

分压网络的另一个用途是产生可变输出电压。如果将电阻 R_2 替换为可变电阻（电位器），则 R_2 上的电压降以及输出电压 V_{\rm OUT} 可以根据电位器滑片的位置而变化，因为此时有一个固定电阻和一个可变电阻。电位器、微调电阻（trimmer）、调压器（rheostat）和可变自耦变压器（variac）都是可变分压装置的例子。

我们还可以更进一步，将固定电阻 R_2 替换为传感器，例如光敏电阻（LDR）。随着光照强度的变化，传感器的阻值变化，输出电压 V_{\rm OUT} 也按比例变化。热敏电阻（thermistor）和应变计（strain gauge）是其他电阻式传感器的例子。

由于上述两种分压表达式都基于相同的公共电流，从数学上它们必然相互关联。因此，对于任意多个串联电阻网络中任一电阻，其两端的电压降可表示为：

电压分压公式

Voltage Divider Equation

% 分压器通用公式 V_{R(x)} = V_{S}\,\frac{R_{x}}{R_{T}} \\ \text{其中：} R_{T} = R_{1} + R_{2} + \cdots + R_{n}

其中： V_{R(x)} 表示电阻 R_x 上的电压降， R_x 为该电阻的阻值， R_T 为串联网络的总电阻。由于各电阻 R 与其对应的电压降 V 成比例关系，该电压分压方程可用于任意多个串联电阻的网络。

请注意，此公式针对无附加负载（无并联支路电流）的理想分压网络。

电压分压示例2

三个阻值分别为 6\,\mathrm{k}\Omega、12\,\mathrm{k}\Omega 和 18\,\mathrm{k}\Omega 的电阻串联连接在 36\,\mathrm{V} 电源两端。计算：

总电阻
流经电路的电流值
各电阻上的电压降

已知数据：

V_{S} = 36\,\mathrm{V},\quad R_{1} = 6\,\mathrm{k}\Omega,\quad R_{2} = 12\,\mathrm{k}\Omega,\quad R_{3} = 18\,\mathrm{k}\Omega.

\begin{aligned} R_{T} &= R_{1} + R_{2} + R_{3} = 6\,\mathrm{k}\Omega + 12\,\mathrm{k}\Omega + 18\,\mathrm{k}\Omega = 36\,\mathrm{k}\Omega,\\ I &= \frac{V_{S}}{R_{T}} = \frac{36}{36000} = 1\,\mathrm{mA},\\ V_{R_{1}} &= V_{S}\,\frac{R_{1}}{R_{T}} = 36\,\frac{6000}{36000} = 6\,\mathrm{V},\\ V_{R_{2}} &= V_{S}\,\frac{R_{2}}{R_{T}} = 36\,\frac{12000}{36000} = 12\,\mathrm{V},\\ V_{R_{3}} &= V_{S}\,\frac{R_{3}}{R_{T}} = 36\,\frac{18000}{36000} = 18\,\mathrm{V}. \end{aligned}

电压分压电路

Voltage Divider Circuit

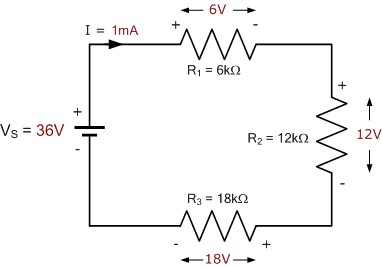
根据基尔霍夫电压定律（KVL），所有三个电阻上的电压降之和应等于电源电压。因此，

V_{T} = 6\,\mathrm{V} + 12\,\mathrm{V} + 18\,\mathrm{V} = 36.0\,\mathrm{V},

与电源电压 V_{S} 的数值相同，计算正确。再次注意，阻值最大的电阻产生最大的电压降the largest voltage drop。

电压分压网络中的抽头点

Tapping Points in a Voltage Divider Network

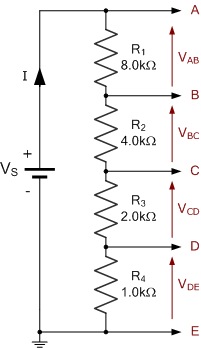
考虑一长串电阻串联并接于电源 V_{S}。在该串联网络上设有电压抽头点 A、B、C、D 和 E。

串联总电阻可通过将各电阻阻值相加得到，总电阻

R_{T} = 15\,\mathrm{k}\Omega.

此总阻值限制了由电源 V_{S} 在电路中驱动的电流。

各电阻上的电压降可用前述公式计算，因此

V_{R1} = V_{AB},\quad V_{R2} = V_{BC},\quad V_{R3} = V_{CD},\quad V_{R4} = V_{DE}.

各抽头点的电压电平相对于地（0\,\mathrm{V}）测量。因此，

V_{D} = V_{DE},\quad V_{C} = V_{CD} + V_{DE},

即点 C 的电位等于电阻 R_{3} 和 R_{4} 上电压降之和。

由此可见，通过选择合适的电阻值，可以从单一电源电压产生一系列按比例分配的电压输出；且由于电源 V_{S} 的负端接地，本例中各输出点电压均为正值。

电压分压示例3

如果将上述串联电阻网络连接到 15 伏直流电源，计算分压电路中每个抽头点的空载输出电压。
\begin{aligned} R_{T} &= R_{1} + R_{2} + R_{3} + R_{4} = 8\,\mathrm{k}\Omega + 4\,\mathrm{k}\Omega + 2\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega = 15\,\mathrm{k}\Omega,\\ V_{AB} = V_{R1} &= V_{S}\,\frac{R_{1}}{R_{T}} = 15\,\mathrm{V}\times\frac{8\,\mathrm{k}\Omega}{15\,\mathrm{k}\Omega} = 8\,\mathrm{V},\\ V_{BC} = V_{R2} &= V_{S}\,\frac{R_{2}}{R_{T}} = 15\,\mathrm{V}\times\frac{4\,\mathrm{k}\Omega}{15\,\mathrm{k}\Omega} = 4\,\mathrm{V},\\ V_{CD} = V_{R3} &= V_{S}\,\frac{R_{3}}{R_{T}} = 15\,\mathrm{V}\times\frac{2\,\mathrm{k}\Omega}{15\,\mathrm{k}\Omega} = 2\,\mathrm{V},\\ V_{DE} = V_{R4} &= V_{S}\,\frac{R_{4}}{R_{T}} = 15\,\mathrm{V}\times\frac{1\,\mathrm{k}\Omega}{15\,\mathrm{k}\Omega} = 1\,\mathrm{V}. \end{aligned}
计算在 B 点与 E 点之间的空载输出电压。
\begin{aligned} R_{T} &= R_{1} + R_{2} + R_{3} + R_{4} = 8\,\mathrm{k}\Omega + 4\,\mathrm{k}\Omega + 2\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega = 15\,\mathrm{k}\Omega,\\ V_{BE} &= V_{S}\,\frac{R_{2} + R_{3} + R_{4}}{R_{T}} = 15\left(\frac{4\,\mathrm{k}\Omega + 2\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega}{15\,\mathrm{k}\Omega}\right) = 7\,\mathrm{V}. \end{aligned}

正负电压分压器

A Negative and Positive Voltage Divider

在上述简单的电压分压电路中，所有输出电压均以公共的零电压地端为参考，但有时需要从单一电源产生正电压和负电压。例如计算机电源中相对于公共参考地端的不同电压等级：-12\,\mathrm{V}、+3.3\,\mathrm{V}、+5\,\mathrm{V} 和 \,+12\,\mathrm{V}。

电压分压示例4

利用欧姆定律，若对空载电压分压电路提供的总电源为 24\,\mathrm{V} 直流，功率为 60\,\mathrm{W}，求为产生 -12\,\mathrm{V}、+3.3\,\mathrm{V}、+5\,\mathrm{V} 和 \,+12\,\mathrm{V} 这几种电压等级所需的电阻 R_{1}、R_{2}、R_{3} 和 R_{4} 的取值。

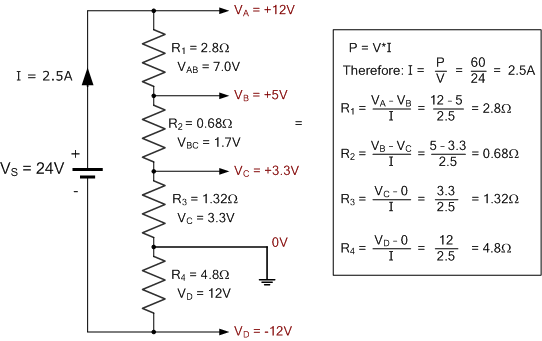
在此示例中，已将零电压接地参考点移动到所需位置，以在保持分压网络跨接于电源的同时产生正负电压。因此，四个电压均相对于该公共参考点进行测量，使得 D 点相对于地呈现所需的 -12\,\mathrm{V} 负电位。

到目前为止，我们已经看到串联电阻电路可用于创建电压分压器（或电位分压网络），该网络在电子电路中应用广泛。通过选择合适的串联电阻值，可获得任何低于输入或电源电压的输出电压。

但除了使用电阻和直流电源来创建无源电阻分压网络外，我们还可以使用电容（C）和电感（L），但此时需采用正弦交流电源，因为电容器和电感器都是无源的“反应性”元件，其阻抗会“反抗”电流的流动。

电容分压器

Capacitive Voltage Dividers

顾名思义，电容分压电路通过在公共交流电源下串联连接的电容器上产生电压降。通常，电容分压器用于将极高电压“降压”，以提供可用于保护或计量的低电压输出信号。如今，高频电容分压器更多地应用于移动电话和平板电脑的显示设备和触摸屏技术中。

与可在交流和直流电源上工作的电阻分压电路不同，电容分压仅在正弦交流电源下可行。这是因为串联电容器之间的电压分配取决于电容的电抗 X_{C}，而该电抗与交流电源的频率相关。

我们在交流电路中有关电容器的教程中了解到，电容器的电抗 X_{C}（以欧姆为单位）与频率和电容成反比，因此由下式给出：

电容电抗公式

Capacitive Reactance Formula

电容电抗的公式为：

X_{C} \;=\;\frac{1}{2\pi f C}

或等价地，用角频率 \omega=2\pi f 表示为

X_{C} \;=\;\frac{1}{\omega C}

其中

X_{C} —— 电容电抗，单位为欧姆（\Omega）；
f —— 交流信号频率，单位为赫兹（Hz）；
\omega —— 角频率，单位为弧度每秒（rad/s）；
C —— 电容，单位为法拉（F）。

因此，通过已知交流电源的电压和频率，我们可以计算各电容的电抗，将其代入上述电阻分压法则的公式，并获得各电容上的相应电压降，如图所示。

电容分压器

Capacitive Voltage Divider

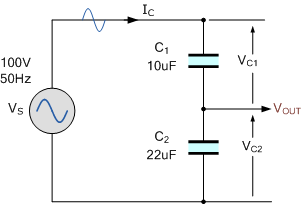
在上述串联电路中，使用两个电容器 10\,\mu\mathrm{F} 和 22\,\mu\mathrm{F}，当它们连接到100\,\mathrm{V}、50\,\mathrm{Hz} 有效值交流电源时，我们可以根据它们的电抗计算出各电容器上的有效值电压降。

\begin{aligned} X_{C_{1}} &= \frac{1}{2\pi f C_{1}} = \frac{1}{2\pi \times 50\,\mathrm{Hz} \times 10\times10^{-6}\,\mathrm{F}} = 318.3\,\Omega,\\ X_{C_{2}} &= \frac{1}{2\pi f C_{2}} = \frac{1}{2\pi \times 50\,\mathrm{Hz} \times 22\times10^{-6}\,\mathrm{F}} = 144.7\,\Omega,\\ X_{C_{T}} &= X_{C_{1}} + X_{C_{2}} = 318.3\,\Omega + 144.7\,\Omega = 463\,\Omega,\\ V_{C_{1}} &= V_{S}\,\frac{X_{C_{1}}}{X_{C_{T}}} = 100\,\mathrm{V}\times\frac{318.3}{463} = 69\,\mathrm{V},\\ V_{C_{2}} &= V_{S}\,\frac{X_{C_{2}}}{X_{C_{T}}} = 100\,\mathrm{V}\times\frac{144.7}{463} = 31\,\mathrm{V}. \end{aligned}

在使用纯电容器时，所有串联电容器上的电压降之和等于电源电压，与串联电阻相同。由于各电容器上的电压降与其电抗成正比，却与电容值成反比，因此较小的 10\,\mu\mathrm{F} 电容器电抗较大（ 318.3\,\Omega），对应的电压降也较大（ 69\,\mathrm{V}）；而较大的 22\,\mu\mathrm{F} 电容器电抗较小（ 144.7\,\Omega），电压降也较小（ 31\,\mathrm{V}）。由于它们串联，电路电流

I_{C} = 216\,\mathrm{mA}

在两电容上相同。

关于电容分压电路的最后一点：只要不存在串联电阻、纯粹由电容构成，两个电容器的电压降（ 69\,\mathrm{V} 和 31\,\mathrm{V}）在数值上就能相加等于 100\,\mathrm{V} 的电源电压，因为它们相位一致。如若两电压不在同相，则不能按基尔霍夫电压定律直接相加，而需对两个电压波形作矢量（相量）相加。

电感分压器

Inductive Voltage Dividers

顾名思义，电感分压器通过串联连接到同一交流电源的电感或线圈上产生电压降。电感分压器可以是将一个线圈分为两部分，并从其中一部分抽取输出电压，也可以是将两组独立线圈串联后抽取输出电压。最常见的例子是在自耦变压器的次级绕组上设置多个抽头。

当用于稳态直流电源或频率接近 0\,\mathrm{Hz} 的正弦波时，电感的电抗几乎为零，表现如短路，直流电流可轻易通过。因此，与电容分压器类似，电感分压也必须在正弦交流电源下进行。串联电感器之间的电压分配可通过各电感的电抗 X_{L} 来计算，而 X_{L} 同样依赖于交流电源的频率。

在交流电路中，我们知道电感电抗 X_{L}（单位：欧姆）与频率和电感量成正比，电源频率越高，电感电抗越大。因此，电感电抗定义如下：

电感电抗公式

Inductive Reactance Formula

X_{L} = 2\pi f L

其中:

X_{L}\ \text{—— 电感电抗，单位：欧姆（\(\Omega\)）；}
\pi \ \text{—— 数值常数，取 }3.142；
f \ \text{—— 频率，单位：赫兹（Hz）；}
L \ \text{—— 电感量，单位：亨利（H）。}

如果我们知道交流电源的电压和频率，就可以计算两个电感的电抗，并将其代入电压分压法则，以获得如图所示的各电感上的电压降。

电感分压器

Inductive Voltage Divider

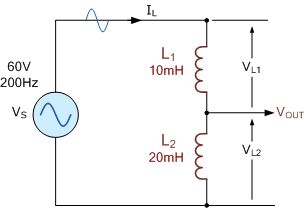
在上述串联电路中，使用两个电感器 10\,\mathrm{mH} 和 20\,\mathrm{mH}，当它们连接到一个 60\,\mathrm{V}、200\,\mathrm{Hz} 的交流有效值电源时，我们可以根据它们的电抗计算出各电容器上的均方根电压降。

\begin{aligned} X_{L_{1}} &= 2\pi f L_{1} = 2\pi \times 200\,\mathrm{Hz} \times 10\times10^{-3}\,\mathrm{H} = 12.56\,\Omega,\\ X_{L_{2}} &= 2\pi f L_{2} = 2\pi \times 200\,\mathrm{Hz} \times 20\times10^{-3}\,\mathrm{H} = 25.14\,\Omega,\\ X_{L_{T}} &= X_{L_{1}} + X_{L_{2}} = 12.56\,\Omega + 25.14\,\Omega = 37.7\,\Omega,\\ V_{L_{1}} &= V_{S}\,\frac{X_{L_{1}}}{X_{L_{T}}} = 60\,\mathrm{V}\times\frac{12.56}{37.7} = 20\,\mathrm{V},\\ V_{L_{2}} &= V_{S}\,\frac{X_{L_{2}}}{X_{L_{T}}} = 60\,\mathrm{V}\times\frac{25.14}{37.7} = 40\,\mathrm{V}. \end{aligned}

与前述电阻和电容分压电路类似，只要不存在串联电阻（即纯电感），所有串联电感器上的电压降之和就等于电源电压。各电感器上的电压降大小与其电抗成正比。

因此，较小的 10\,\mathrm{mH} 电感器电抗较小（ 12.56\,\Omega），对应的电压降也较小，为 30\,\mathrm{V}；而较大的 20\,\mathrm{mH} 电感器电抗较大（25.14\,\Omega），电压降为 40\,\mathrm{V}。串联电路中的电流 I_{L}=1.6\,\mathrm{mA}，由于 L_{1} 与 L_{2} 串联，该电流在两者上相同。

分压法则总结

我们已经看到，电压分压器或电位分压网络是一种非常常见且有用的电路配置，它允许我们从单一电源产生多个不同的电压等级，从而无需为电路中不同电压需求的部分使用独立电源。

顾名思义，电压或电位分压器就是通过电阻、电容或电感，将固定电压“分割”为精确比例的输出电压。最基本且最常用的分压电路是两个定值电阻串联，但也可通过调节电位器（或调压器）的滑触点来实现可变分压。

分压电路的一个常见应用是将其中一个定值电阻替换为传感器。光敏传感器、温度传感器、压力传感器和应变计等阻性传感器会随着环境变化而改变其阻值，可置于分压网络中提供模拟电压输出。此外，双极晶体管和 MOSFET 的偏置电路也常使用分压器。

附录

分压器分类

分压器类型	原理及组成	典型元件	使用场景
电阻分压器	串联电阻按阻值比例分压	定值电阻	• 产生基准电压 • ADC 输入信号衰减 • 晶体管偏置
电容分压器	串联电容按电抗比例分压	电容器	• 高频电压取样 • 显示屏/触摸屏驱动 • 无源滤波
电感分压器	串联电感按电抗比例分压	电感器（线圈）	• 自耦变压器抽头 • 高频电源分配 • 射频谐振网络
可变电位器（Rheostat）	带滑触点的可调电阻分压	旋钮式电位器、微调电阻	• 音量/亮度调节 • 校准与调零 • 可变参考电压
传感器分压器	用阻性传感器替换固定电阻，阻值随环境变化	光敏电阻（LDR）、热敏电阻、应变计	• 光强检测 • 温度测量 • 压力/力值检测
R-2R 阻阻网络	多级串并联电阻构成阶梯分压	R、2R 电阻阵列	• 数模转换器（DAC） • 数字微调电压输出
齐纳稳压分压	限流电阻+齐纳二极管分压	齐纳二极管 + 限流电阻	• 简易稳压电源 • 参考电压源
有源缓冲分压	分压后加运放缓冲、提升输入阻抗或精度	运算放大器 + 分压电阻	• 高精度电压检测 • 隔离低阻抗负载 • 低温漂应用

单词表

英文术语	中文翻译
Voltage Divider	电压分压器
Potential Divider	势垒分压器
Voltage Divider Rule	电压分压法则
Potentiometer	电位器
Rheostat	调压器
Sensor Divider	传感器分压器
Light Dependent Resistor (LDR)	光敏电阻
Thermistor	热敏电阻
Strain Gauge	应变计
Resistor	电阻器
Resistance	电阻
Series	串联
Current	电流
Voltage Drop	电压降
Supply Voltage	电源电压
No-load	空载
Load	负载
Tap / Tapping Point	抽头（点）
Ground	地（接地）
Reference	参考（点）
Kirchhoff’s Voltage Law (KVL)	基尔霍夫电压定律
Ohm’s Law	欧姆定律
Capacitive Voltage Divider	电容分压器
Capacitive Reactance (Xₙ)	电容电抗
Inductive Voltage Divider	电感分压器
Inductive Reactance (Xₗ)	电感电抗
Reactive Component	无源（反应性）元件
AC Supply	交流电源
DC Supply	直流电源
RMS	有效值
R-2R Network	R-2R 阻阻网络
DAC (Digital-to-Analog Converter)	数模转换器
ADC (Analog-to-Digital Converter)	模数转换器
Zener Divider	齐纳稳压分压
Active Buffer Divider	有源缓冲分压

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。

Menu

Share

15.电压分压器

电压分压器