基尔霍夫电压定律

基尔霍夫电压定律（KVL）是基尔霍夫第二条定律，涉及闭合电路路径上的能量守恒。 古斯塔夫·基尔霍夫的电压定律是我们用于电路分析的两条基本定律中的第二条。它指出，对于任何闭合回路，沿着该回路上所有电压的代数和等于零。因为电路回路是一个闭合的导电路径，所以不存在能量的损失。

换句话说，沿回路的所有电势差的代数和必须满足：

这里的代数和意味着要考虑电源和电压降的极性和符号。

基尔霍夫提出的这一思想通常称为“能量守恒”：在闭合回路中移动时，最终会回到起始点，并且回到相同的初始电位，因此回路上不会有电压损失。因此，回路上的任何电压降之和都必须等于沿途遇到的任何电源电压之和。

在将基尔霍夫电压定律应用于具体电路元件时，必须特别注意元件两端电压降和电动势的代数符号（+ 和 –），否则计算可能会出错。

但在深入研究基尔霍夫电压定律（KVL）之前，让我们先了解单个元件（如电阻器）上的电压降。

单个电路元件

A Single Circuit Element

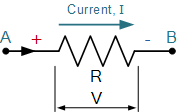
在这个简单的例子中，我们假设电流 I 的方向与正电荷的流动方向一致，也就是常规电流方向。

此处电流通过电阻器的流向是从点 A 到点 B，即从正极流向负极。因此，当我们沿着电流方向移动时，电阻元件上的电势会下降，产生一个 -I R 的电压降。

如果电流方向相反，从点 B 流向点 A，那么由于我们是在从负电位移动到正电位，就会在电阻元件上产生一个 +I R 的电压升。

由此可见，要正确应用基尔霍夫电压定律，必须首先明确极性方向——电阻元件上的电压降符号取决于电流的流动方向。一般原则是：沿电流方向穿过元件时电势下降，而沿电动势源的方向移动时电势上升。

对于闭合电路中的电流方向，可以假设为顺时针或逆时针，任选其一。如果所选方向与实际电流方向相反，计算结果依然正确，只是在代数结果前会带上负号。

为了更好地理解这一点，下面我们来看一个单环电路，验证基尔霍夫电压定律是否成立。

单个环路电流

A Single Circuit Loop

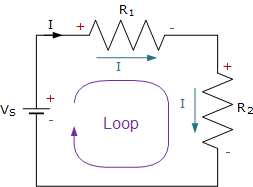
基尔霍夫电压定律指出，在任何回路中，所有电势差的代数和必须等于零，即： \Sigma V = 0。由于两个电阻 R_1 和 R_2 串联，它们属于同一回路，因此相同的电流必须流过每个电阻。由此，电阻 R_1 上的电压降为 I \times R_1，电阻 R_2 上的电压降为 I \times R_2，由 KVL 可得：

我们可以看到，将基尔霍夫电压定律应用于该单一闭合回路，可以推出串联电路的等效电阻或总电阻公式

并且我们可以在此基础上进一步推导出回路中各处的电压降值。

基尔霍夫电压定律示例 1

三个电阻 R_1 = 10\,\Omega、R_2 = 20\,\Omega 和 R_3 = 30\,\Omega 串联连接在一个理想 12\,\mathrm{V} 直流电池两端。计算： a) 总电阻 b) 电路电流 c) 每个电阻上的电流 d) 每个电阻上的电压降 e) 验证基尔霍夫电压定律（KVL）成立

a) 总电阻 R_T

b) 电路电流 I

c) 每个电阻上的电流 串联电路中电流相同，因此

d) 每个电阻上的电压降

e) 验证基尔霍夫电压定律 根据 KVL，有

代入数值：

因此基尔霍夫电压定律得以验证。

基尔霍夫环路

Kirchhoff’s Circuit Loop

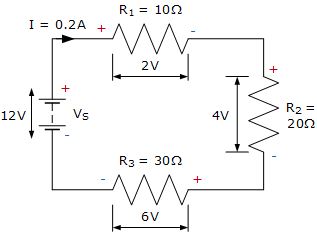
我们已经看到，基尔霍夫电压定律（KVL）是基尔霍夫的第二条定律，它规定：当你从某一固定点出发，沿闭合电路回到同一点时，考虑极性后，沿途所有电压降的代数和总是零。即：

基尔霍夫第二定律背后的理论也称为电压守恒定律；在处理串联电路时，这一点尤为有用，因为串联电路同时也起到分压器的作用，而电压分压电路是许多串联电路的重要应用。

附录

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。