节点、回路与支路
Nodes Loops and Branches
节点、回路与支路是组成电路的三大基本要素,使我们能够运用各种电路求解技术来简化复杂网络。
电路的节点、回路与支路
Electrical Nodes, Loops and Branches of a Circuit
节点、回路与支路是电路与网络中三个基本概念,帮助我们理解电流如何在其中流动。要运用不同的电路定理来分析复杂网络,就必须先掌握这些基本概念与术语。
电路或电气网络本质上是由各种电路元件(如电阻器、电容器、功率源等)组成的集合,这些元件通过导线互相连接,形成一条或多条导电路径,使电流得以流动。
严格来说,电路或网络是一条完整的回路或回路的组合,电能得以在其中传输。在分析此类复杂网络时,特别是应用基尔霍夫电压定律(Kirchhoff’s Voltage Law, KVL)和基尔霍夫电流定律(Kirchhoff’s Current Law, KCL),必须识别并使用节点、回路与支路的概念。
你也可以将电路与网络看作是电能流动的地图:网络是道路与交叉路口的集合,而电路则是交通系统(电流沿道路流动),电能从电源流向各元件和负载,再返回电源。换言之,电气网络是电阻器、电感器、电容器以及电压源、电流源等多种元件的互连。
当强调电路的功能时,指的是电流的预期流动;当强调网络的结构时,指的是电源、元件与负载之间连接方式,描述为路径(path)、网孔(mesh)、节点(node)、回路(loop)和支路(branch)等术语。
常见电路理论术语:
Common Electrical Circuit Theory Terminology
❖ 电路 (Circuit) —— 任意一个闭合的导电回路,电流可在其中流动。
❖ 网络 (Network) —— 由元件、电源和负载组成的集合,其间转换、消耗或储存电能。
❖ 路径 (Path) —— 一条由元件或电源串联组成的线路,且其中不重复经过同一节点。
❖ 节点 (Node) —— 电路中两个或多个元件相接之处,也称连接点或端点。
❖ 支路 (Branch) —— 连于一对节点之间的一个或一组元件(如电阻器或电源)。
❖ 回路 (Loop) —— 电路中不重复经过任何元件或节点的简单闭合路径。
❖ 网孔 (Mesh) —— 电路中的一个闭合回路,且其内部不包含其他回路或路径。
注意:这些定义与术语在各种电路定律和分析技术中被频繁使用,理解它们至关重要。
节点
Nodes In A Circuit
在电路中,节点(或称节点点)是两个或多个元件相连之处。节点表示电流可以在此分流或汇合的位置。
电气节点A示例
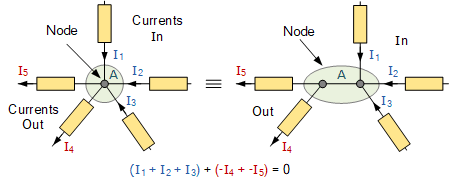
左侧图像显示了一个单节点(A),有五个元件都连接到该节点。该节点在各条导线和元件汇合处用一个 “实心点” 标示。通常,用实心点来表示各元件之间的实际连接(结点)。
需要注意的是,在示意图中,结点并不一定要用一个点来表示元件之间的连接。不同导线之间的交叉处也可以不相连,而是用“桥接”线bridge来表示它们不相交。
右侧图像则将单一结点(A)分成了两个由零电阻导线相连的连接点。虽然你可能认为这里出现了两个结点,但事实并非如此。
所做的仅仅是将原本的公共结点(A)拆分成一条零电阻的导线,所有元件都连接到这条导线上:一侧两个元件,另一侧三个元件。两幅图在电路意义上是等价的,都表示同一个结点 “A”。
在理想情况下,假设导线电阻为零(0\Omega),结点内的所有点都具有相同的电压电位。然而,我们必须记住,流入结点的所有电流代数和等于流出同一结点的所有电流代数和。
流入流出结点的电流称为支路电流,因为支路是网络中两结点之间的单一路径。支路电流即在一对结点之间流动的电流。
因此,在上述例子中,流入和流出结点 “A” 的支路电流代数和为零。如果将流入电流取为正,流出电流取为负,则有:
由此我们可以得到:
因此,根据基尔霍夫电流定律(Kirchhoff’s Current Law,KCL),流入结点的电流代数和等于流出结点的电流代数和。该电流和的思想在交流电路分析中依然成立,但必须使用矢量相加,因为简单地对电流大小相加并不能产生正确结果,而直流电路分析中可以这样做。
节点电压
Node Voltage
如前所述,我们可以假设同一节点内的所有点对于直接连接到该节点的所有元件都具有相同的电压电位。也就是说,物理上连接到同一节点的每一个元件的连接点,其电压值完全相同。即使该节点被分成多个接点,也不存在电位差。
在电路理论中,假设节点的连接导线是理想的、具有零电阻(0\Omega)是一个基本思想,这使我们能够将元件归并到同一节点,并为该节点赋予单一的电压值。节点电压通常相对于参考节点(通常是接地)来测量。注意,参考节点的电压默认总是被定义为零,除非另有说明。
此外,一旦节点电压已知,我们就可以利用它们来计算任意两节点之间的各种支路电压、电流和功率。这可以通过节点电压法或直接应用欧姆定律进行电路分析。
支路
Branches Of A Circuit
支路是电路中连接两个节点(接点)之间、包含单个元件或多个串联元件的任何一条路径。因此,支路可以由两个或多个串联元件组成。
例如,两个节点之间连接的单个电阻器即被视为一个支路;如果在该电阻器串联再加上第二个电阻器(或其他元件),那么这两个串联元件的组合仍然构成一个支路,因为流经两者的电流相同,路径只有一条。
本质上,支路即是电路中电流在两节点之间只有一条路径可循的那部分。因此,每一支路只承载一条电流,尽管该电流可能是由多个电流源在其他节点合流或分流后形成的。
节点AB之间的支路节点示例
Example of a Branch Between Nodes “A” and “B”
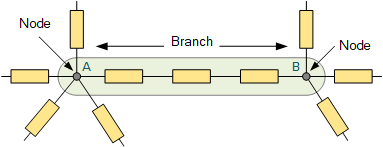
在这里,电流在节点 “A” 和节点 “B” 之间通过单一路径流动,形成一个支路,该支路中任意数量的元件连接在同一对节点之间。虽然该支路可视为一个简单的串联电路,流经它的电流相同,但我们也可以在两节点间并联多个支路,此时任意数量的元件都可并联连接在同一对节点之间。
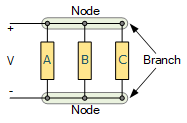
如果两个或更多电路元件并联连接,则每个元件的两端都直接连接到同一对节点上。由于电路元件通常具有两个端子,因此每个并联支路上的电压都与其他任何并联支路上的电压相同。
也就是说,若电路中某些元件在同一对节点之间具有相同的电压,则称它们为并联连接,如下所示。
显然,尽管每个并联元件上的电压在大小和极性上都相等,但各支路的电流可能不同。
回路
现在,让我们来讲回路。回路是电路中从同一节点开始并在该节点结束的任意一条简单闭合路径。换句话说,回路形成一个完整的闭合电路,该电路中任意节点只经过一次,起点和终点相同。就像在电路中行走,从节点 “A” 出发,经过一系列节点和元件后回到起点 “A” 一样,如下图所示。
单回路电路示例
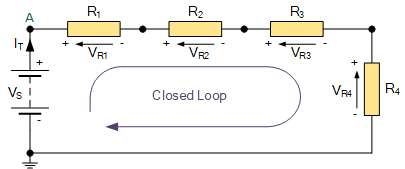
在上图的简单单回路电路中,电池与四个电阻串联连接,因此电路中只有一个闭合回路,电流可在其间流动,且共有五个节点。此处假设回路电流 I_T 沿时针方向流动。对于电路分析,需要为所有回路指定相同的方向,可选时针或逆时针。
请注意,回路可以很大,涵盖电路的多个部分,也可以是嵌套在较大电路中的更小回路。此外,回路不必包含任何元件,它只需是一条闭合路径。
回路是一个基本概念,尤其在应用基尔霍夫电压定律(Kirchhoff’s Voltage Law,简称 KVL)分析电路时尤为重要。基尔霍夫电压定律指出,任意闭合回路中所有电压降的代数和为零。该示例显然是串联电路,因为相同的电流 I_T 流经所有电阻。
串联电阻适用于电压分配(或分压)规则,因此各电阻上的电压降之和等于电源电压,即:
由于 KVL 可表示为 \sum V = 0,则有:
如果需要,还可以用电阻值表示回路中任意电阻上的电压降:
电路中的网孔
Mesh in the Electric Circuit
除了节点、回路和支路之外,网孔(Mesh)也是电路分析中的一个基本概念,尤其在使用网孔(回路)分析法(Mesh Analysis)时非常常见。基本上,网孔是电路中不包含或封闭任何其他回路的回路。换句话说,它是在电路中可沿着一条闭合路径追踪、且不跨越或穿过其他元件或回路的最小闭合回路。如图所示,网孔内部不包含任何额外元件。
形成网孔的节点、回路与支路
Nodes, Loops and Branches Forming a Mesh
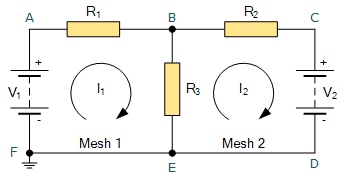
在上面的这个简单示例中,我们有一个双网孔电路,分别标识为“网孔 1”和“网孔 2”。路径 A\text{–}B\text{–}E\text{–}F\text{–}A 形成的回路是一个网孔,路径 B\text{–}C\text{–}D\text{–}E\text{–}B 形成的回路也是一个网孔。显然,这两个回路 A\text{–}B\text{–}E\text{–}F\text{–}A 和 B\text{–}C\text{–}D\text{–}E\text{–}B 都可被视为独立网孔,因为它们都无法再细分为更小的回路(网孔)。
然而,外部回路 A\text{–}B\text{–}C\text{–}D\text{–}E\text{–}F\text{–}A 虽然是根据基尔霍夫电压定律可以分析的有效回路,但由于它将两个内网孔包围在其内部,因此不能称为网孔。由此可见,“网孔”与“回路”虽然都是闭合路径,但网孔是不包含其他回路的最小闭合路径,所以所有网孔都是回路,却并非所有回路都是网孔。
由此,我们可以识别出该电路具有:
5 个节点 \;A,\;B,\;C,\;E,\;F,(注意点 D 和 E 被视为同一分裂节点)
5 条支路 \;V_1,\;R_1,\;R_2,\;R_3,\;V_2
2 个网孔(网孔 1 和 网孔 2)
每个网孔都分配有自己的网孔电流用于分析;为方便起见,已将网孔电流 I_1 和 I_2 设定为顺时针方向。
节点、回路与支路 — 综合运用
Nodes, Loops and Branches – Putting Them All Together
既然我们已经理解了节点、回路与支路的基本概念,就可以看到,电源与元件的连接所形成的支路网络互联各节点(汇点),从而构建出如图所示的内部网孔。
电路的电气节点、回路与支路
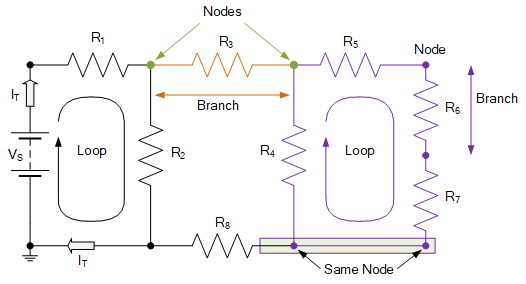
任何给定网络的支路电流和节点电压的行为,都基于基尔霍夫的两条基本定律: 节点定律(Nodal Law)——流入某一节点的支路电流之和等于流出该节点的支路电流之和:
网孔定律(Mesh Law)——沿任一闭合网孔(或回路)的电压降之和为零:
节点、回路与支路教程总结
我们已经看到,基本的电路元件和组件可以相互连接,形成电气电路或网络,其互连关系可用节点、回路与支路来描述。
节点、回路与支路背后的概念与思想,是帮助我们理解电能如何在网络中流动的基础,从而能够应用基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)来分析并求解复杂电路。
我们还看到,节点之间的连接形成了一条路径,而单一回路则可归类为网孔。支路表示任何具有两个端子的单一元件(如电压源或电阻),其两端分别连接于一对节点。
综上,这些概念有助于描述电路的结构与行为:
节点 告诉我们元件的连接位置以及电流如何分流;
支路 给出了电流流过的线路段及各连接点之间的电压降;
回路 与 网孔 则让我们能够沿电路中的闭合路径追踪,以理解电压如何相加或相互抵消。
附录
单词表
声明
本文仅供学习,禁止用于任何的商业用途。

