磁学
Magnetism
电磁学Electromagnetism是在电流通过简单导体(例如一段导线或电缆)时产生的力。 虽然磁体可以由吸引(和排斥)其他材料(主要是金属)的铁磁材料制成,但磁性本身是磁体在相互吸引或排斥时所施加的力。当电流流经导体时,导体周围会产生一个小的磁场,其“北”极和“南”极的方向由电流流向决定。
磁性在电气与电子工程中起着重要作用,因为若没有它,继电器、螺线管、电感器、扼流圈、线圈、扬声器、电动机、发电机、变压器和电度表等组件就无法工作。
当电流流过任何一圈线圈时,都利用了电磁学效应。但在深入研究磁学,尤其是电磁学之前,我们需要回忆一下物理课上关于磁体及磁性如何工作的原理。
磁性的本质
The Nature of Magnetism
天然状态下的磁体以磁性矿石形式存在,主要有两种:磁铁矿,也称“氧化铁”( \mathrm{Fe_3O_4}),以及磁石,也称“leading stone”。如果将这两种天然磁体悬挂在绳子上,它们会沿地球磁场定向,总是指向北方。 一个很好的例子是指南针的指针。对于大多数实际应用而言,这些天然磁体可以被忽略,因为它们的磁性非常弱;而如今可以制造出各种形状、尺寸和磁力的人工磁体。
基本上有两种形式的磁性:“永久磁体”和“暂磁磁体”,其使用类型取决于具体应用。用于制作磁体的材料有多种,如铁、镍、镍合金、铬和钴等;在自然状态下,这些元素(例如镍和钴)单独表现出非常微弱的磁性。
然而,当它们与其他材料(例如铁或过氧化铝)混合或“合金”在一起时,就会变成非常强的磁体,并产生诸如“alcomax”、“hycomax”、“alni”和“alnico”等商用名称。
在未磁化状态下,磁性材料的分子结构呈松散的磁性链或个别微小磁体以随机方式排列。这种排列的整体效果导致零或非常弱的磁性,因为这些杂乱无章的分子磁体排列会相互抵消。
当材料被磁化Magnetised时,这种随机的分子排列会发生变化,微小的未对齐且随机的分子磁体会排列成有序的磁链magnetic arrangement。这种铁磁材料分子排列的思想称为韦伯理论,并在下方示意图中说明。
铁块与磁铁的分子磁性排列
Magnetic Molecule Alignment of a Piece of Iron and a Magnet
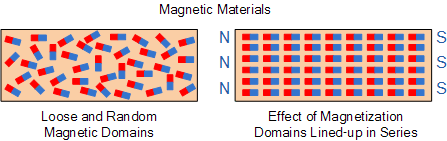
韦伯理论基于这样一个事实:所有原子由于其电子的自旋作用而具有磁性。原子群会相互结合,使它们的磁场都朝同一方向旋转。磁性材料在分子层面上由围绕原子的微小磁体群组成,被磁化的材料会使其大部分微小磁体仅沿一个方向排列,从而在一个方向产生北极,在另一个方向产生南极。
同样,如果材料的微小分子磁体指向各个方向,那么这些分子磁体会被相邻的磁体相互中和,从而抵消任何磁效应。这些分子磁体区域称为磁畴domains。
任何磁性材料都会自行产生磁场,其强度取决于材料中磁畴的排列程度,该排列由轨道电子和自旋电子共同作用形成。此排列程度可以用称为磁化强度M的量来描述。
在未磁化的材料中,M=0,但当外加磁场撤除后,仍有部分磁畴在材料的小区域内保持排列。对材料施加磁化力的作用是使部分磁畴排列一致,从而产生非零的磁化强度值。
一旦磁化力被移除,材料内部的磁性会根据所用材料的不同而或保持存在,或较快衰减。这种材料保持磁性的能力称为剩磁(Retentivity)。
需要保持磁性的材料具有较高的剩磁,因此常用于制造永久磁铁;而需要迅速失去磁性的材料(例如用于继电器和螺线管的软铁芯)则具有非常低的剩磁。
磁通
Magnetic Flux
所有磁体,无论形状如何,都具有两个区域,称为磁极magnetic poles;磁路中的磁性在其内部和周围产生一条有序且平衡的看不见的磁力线链。这些磁力线统称为磁体的“磁场”。磁场的形状在不同区域的强度不同,磁体中磁性最强的区域称为“极”。每个磁体的两端各有一个磁极。
这些磁力线(称为矢量场)肉眼不可见,但可以通过将铁屑撒在纸上或使用小型指南针沿线追踪来直观地观察到。磁极总是成对出现:一端称为北极(North‐pole),另一端称为南极(South‐pole)。
磁场通常以力线的形式直观显示,它们在材料两端最密集、最集中的区域形成明显的磁极。组成磁场的这些线条既表示方向,也表示强度,称为“力线”(Lines of Force),更常称为“磁通”(Magnetic Flux),用希腊字母 \Phi 表示。
条形磁铁磁场的磁力线图
Lines of Force from a Bar Magnets Magnetic Field
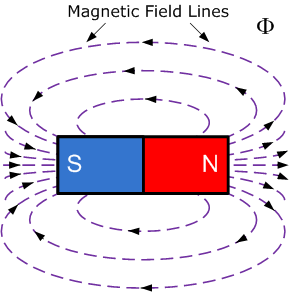
如上所示,当磁通线更为密集时,磁体极附近的磁场最强。磁通的一般方向是从北极(N)指向南极(S)。此外,这些磁力线形成闭合回路,从磁体的北极出发,在南极进入。磁极总是成对出现。
然而,磁通实际上并不会从北极“流向”南极,也不会“流动”到任何地方,因为磁通是围绕磁体存在的一个静态区域,其中存在磁力。换言之,磁通不会移动,它只是存在,并且不受重力影响。在绘制磁力线时,有一些重要规律:
磁力线永不交叉;
磁力线是连续的;
磁力线总是形成闭合回路;
磁力线具有明确的方向,由北极指向南极;
磁力线越密集,表示磁场越强;
磁力线越稀疏,表示磁场越弱。
磁力与电力类似,具有吸引和排斥作用。当两组磁力线彼此靠近时,两个磁场的相互作用会产生以下两种情况之一:
当相邻磁极相同时(北–北或南–南),它们会排斥;
当相邻磁极相反时(北–南或南–北),它们会吸引。
这种现象可用著名的“异性相吸”来记忆。利用铁屑实验可以直观地展示这种磁场相互作用,显示磁体周围的磁力线分布。下图展示了同极排斥与异极吸引对磁场的影响。
同极与异极的磁场示意图
Magnetic Field of Like and Unlike Poles
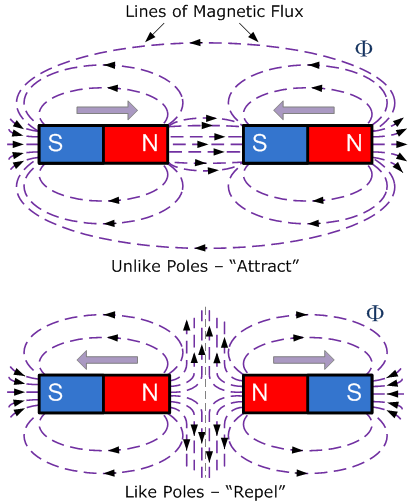
当用指南针绘制磁力线时,可观察到磁力线的产生方式在磁体两端各自形成一个明确的极:磁力线在北极处分离而出,在南极处重新进入。磁性可以通过加热或锤击磁性材料来破坏,但仅仅将磁体掰成两块并不能破坏或隔离磁性。
因此,如果将一个普通的条形磁铁掰成两块,你并不会得到两块各自只有一半磁性的碎片,而是每块碎片都将以某种方式拥有自己的北极和南极。若再将其中一块继续掰成两块,每一更小的碎片仍将具有一个北极和一个南极,如此循环下去。无论磁铁被掰得多小,每一块都仍具有北极和南极,的确令人惊奇!
为了在电气或电子计算中利用磁性,我们需要定义磁性的各个方面。
磁性的量值
The Magnitude of Magnetism
我们现在知道,磁性材料周围的磁通(磁力线)用希腊字母 \Phi 表示,其单位为韦伯( \mathrm{Wb}),以纪念 Wilhelm Eduard Weber。单位面积内的磁力线数量称为“磁通密度”,由于磁通 \Phi 的单位为 \mathrm{Wb},面积 A 的单位为 \mathrm{m}^2,因此磁通密度的单位为
,符号为 B。
然而在磁学中,磁通密度使用特斯拉(\mathrm{T})作为单位,即
磁通密度与磁力线数量成正比,与面积成反比,因此可以定义磁通密度为:
磁通密度 (Magnetic Flux Density)
磁通密度的符号为 B,其单位为特斯拉(\mathrm{T})。
重要的是要记住,所有关于磁通密度的计算都必须使用相同的单位,例如:磁通以韦伯(\mathrm{Wb})表示,面积以平方米( \mathrm{m}^2)表示,磁通密度以特斯拉(\mathrm{T})表示。
磁学示例 1
在一根圆形磁棒中测得磁通量 \Phi = 0.013\ \mathrm{Wb}。若该材料的直径为 12\ \mathrm{cm},求磁通密度。
材料的横截面积为
由磁通 \Phi = 0.013\ \mathrm{Wb},可得磁通密度
因此,磁通密度为
在电路磁学中,须记住:一特斯拉(\mathrm{T})定义为垂直于磁场方向的导体通以 \,1\ \mathrm{A} 电流时,在单位长度上所受的力为 \,1\ \mathrm{N}。这将在下一个“电磁学”教程中演示。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

