谐波
Harmonics
谐波是叠加在基波上的不需要的高次频率,会导致波形失真。
谐波与谐波失真指的是理想正弦波——电源电压或负载电流波形应有的样子——与由于非线性负载而实际上所呈现波形之间的差异。
在交流电路中,电阻的行为与直流电路完全相同。也就是说,流过电阻的电流与加在其两端的电压成正比。这是因为电阻是一种线性元件,如果施加在它上的电压是正弦波,那么流过它的电流也将是正弦波,二者之间的相位差为零。
通常,在处理电路中的交流电压和电流时,假设它们是纯粹且呈正弦形状的,仅存在一个频率分量,称为“基波频率”,但情况并非总是如此。
在某些电气或电子器件或电路中,其电压—电流特性并非线性,即流过它的电流并不与所加电压成正比。与该器件相关的交流波形将在不同程度上偏离理想正弦波,这类波形通常称为非正弦波或复杂波形。
复杂波形由常见的电气设备产生,例如带铁心的电感器、开关变压器、荧光灯中的电子镇流器以及其他诸如大电感负载的设备,以及交流同步发电机、发电机组和其他类似电气机械的输出电压和电流波形。其结果是,即使电压波形是正弦波,电流波形也可能不是正弦波。
此外,大多数电子电源开关电路(如整流器、可控硅(SCR)、功率晶体管、功率转换器以及其他将电源正弦波切割和分段以控制电机功率或将交流电转换为直流电的固态开关)往往仅在交流电源的峰值处抽取电流。由于这些开关电路的电流波形是非正弦的,因此其负载电流被认为包含谐波。
非正弦复杂波形是通过“叠加”一系列称为“谐波”的正弦波频率来构成的。谐波是用于描述不同频率波形对正弦波失真的一般术语。
无论复杂波形的形状如何,都可以在数学上将其分解为基波频率和若干“谐波频率”这几个分量。但我们所说的“基波频率”究竟是什么意思呢?
基波频率
Fundamental Frequency
基波波形(或第一谐波)是具有电源频率的正弦波。基波是构成复杂波形的最低或基本频率 f,因此所得到的复杂波形的周期时间 T 将等于基波频率的周期时间。
让我们考虑如图所示的基本基波(或第一谐波)交流波形。
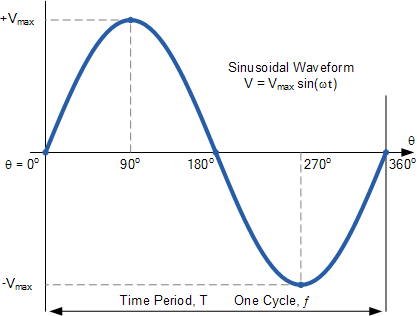
其中:
V_{max} 是峰值电压(单位:伏特volts), f是波形的频率(单位:赫兹Hertz, Hz)。
我们可以看到,正弦波是一种交变电压(或电流),其幅值随角度 2\pi f 的正弦函数变化。波形的频率 f由每秒完成的周期数决定。在英国,这一基波频率定为 50 Hz;而在美国,则为 60 Hz。
谐波是以基波频率的整数倍(整数倍频)运行的电压或电流。因此,对于 50 Hz 的基波而言:
二次谐波频率为 100 Hz(2 × 50 Hz)
三次谐波频率为 150 Hz(3 × 50 Hz)
五次谐波频率为 250 Hz(5 × 50 Hz)
七次谐波频率为 350 Hz(7 × 50 Hz)
依此类推。对于 60 Hz 的基波,二次、三次、四次和五次谐波频率分别为 120 Hz、180 Hz、240 Hz 和 300 Hz。
换言之,“谐波”就是基波频率的倍频,可表示为 2f,3f,4f 等等。
谐波引起的复杂波形
Complex Waveforms Due To Harmonics
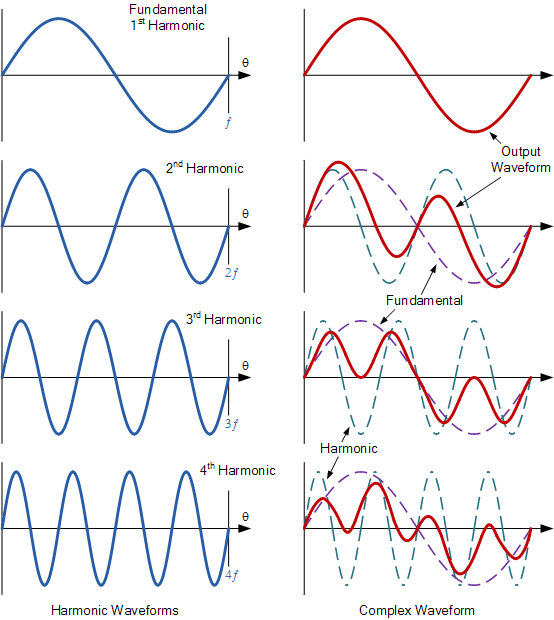
注意,上图中的红色波形表示由于谐波成分叠加到基波上时,负载所看到的实际波形。
基波波形也称为第一谐波波形。因此,第二谐波的频率是基波频率的两倍,第三谐波的频率是基波的三倍,第四谐波的频率是基波的四倍,如左侧列所示。
右侧列显示了基波与不同谐波频率的谐波波形叠加后所产生的复杂波形。注意,结果复杂波形的形状不仅取决于所存在谐波频率的数量和幅值,还取决于基波与各谐波之间的相位关系。
我们可以看到,复杂波是由基波加上若干谐波组成,每个谐波都有其自身的峰值和相位角。例如,如果基波表示为:
则谐波的值为:
二次谐波:
三次谐波:
四次谐波:
依此类推。
那么,复杂波形的表达式将为:
谐波通常按其名称和频率进行分类,例如基波的二次谐波(100 Hz),也按其序列进行分类。谐波序列是指在平衡的三相四线制系统3-phase 4-wire system中,谐波电压和电流相对于基波波形的相量旋转。
正序谐波positive sequence harmonic(4次、7次、10次……)会以与基波相同的方向(正向)旋转;
负序谐波negative sequence harmonic(2次、5次、8次……)则以与基波相反的方向(逆向)旋转。
一般而言,正序谐波是不受欢迎的,因为它们叠加到波形上,会导致导线、输电线路和变压器过热。
另一方面,负序谐波在各相之间循环,由于相反的相量旋转,它们会削弱电机(尤其是感应电机)所需的旋转磁场,导致机械转矩下降。
另一类特殊谐波称为“三倍频谐波”(triplens),即基波三倍的谐波(3次、6次、9次……),因此相位位移为零度,也称零序谐波。零序谐波在各相与中性线或地之间循环。
正序,负序,零序谐波的证明可以参考附录中的三相对称分量
与能相互抵消的正序和负序谐波不同,三次谐波及其倍数不会相互抵消,而是在公共中性线上算术叠加,中性线同时承受来自三相的电流。
结果是,中性线中的谐波电流幅值可能达到基波相电流幅值的三倍,导致效率降低并过热。
我们可以将序列效应按50 Hz基波的倍频总结如下:
谐波序列
请注意,相同的谐波序列也适用于 60 Hz 的基波波形。
总结
谐波是在基波频率(即电路工作频率)上叠加的较高频率波形,这些波形足以使基波波形发生畸变。基波所受的畸变程度完全取决于现存谐波的类型、数量和波形。
在过去几十年里,随着电机、风扇和水泵的电子调速器、电源开关电路(如整流器、功率转换器和晶闸管功率控制器)以及大多数非线性电子相位控制负载和高频(节能)荧光灯的引入,谐波才大量出现。这主要是因为这些负载在工作时所需的电流并不忠实跟随正弦交流电源波形,如整流器或功率半导体开关电路那样。
电力配电系统中的谐波与基波(50 Hz 或 60 Hz)电源叠加,造成电压和/或电流波形的畸变。这种畸变形成了由多个谐波频率组成的复杂波形,可能对电气设备和输电线路产生不利影响。
决定复杂波形特征形状的畸变程度,直接与最主要的谐波成分的频率和幅值相关,而这些谐波频率都是基波频率的整数倍。最主要的谐波成分为从二次谐波到十九次谐波,其中三倍频谐波(triplens)影响最严重。
附录
三相对称分量
1. 定义旋转算子
令
则显然有
2. 第 n 次谐波的三相相量
设第 n 次谐波峰值为 E_{n\max},则三相相量可写为
3. 利用 a^3=1 做模 3 运算
因此只需看 n 除以 3 的余数:
若 n \bmod 3 = 1,则 a^n=a,即相位依次为
A\to0^\circ,\quad B\to -120^\circ,\quad C\to -240^\circ与基波正序(相序 A→B→C)相同,称正序谐波。
若 n \bmod 3 = 2,则 a^n=a^2,即相位依次为
A\to0^\circ,\quad B\to -240^\circ\;(=+120^\circ),\quad C\to -480^\circ\;(=-120^\circ)与基波相序相反(A→C→B),称负序谐波。
若 n \bmod 3 = 0,则 a^n=1,三相同相位
A=B=C=0^\circ称零序谐波(Triplens)。
THD
总谐波失真(Total Harmonic Distortion,THD) 是衡量波形中谐波含量的指标,用来表示所有高次谐波分量相对于基波分量的总畸变程度。
1. 定义与公式
电压总谐波失真(V-THD):
电流总谐波失真(I-THD):
其中:
V_1,\,I_1 为基波(1st harmonic)的有效值(RMS)。
V_n,\,I_n 为第 n 次谐波的有效值( n\ge2)。
通常将 THD 表示为百分比:
2. 意义
反映波形畸变程度
THD 越大,表示高次谐波含量越多,波形偏离理想正弦波越严重。
影响电能质量
高 THD 会导致变压器和电动机额外发热、效率下降;
增加电力系统损耗、降低功率因数;
对敏感电子设备(如UPS、伺服驱动)产生干扰甚至损坏。
法规与标准
IEC 61000-3-2 对 ≤16 A/相 的电源设备规定 ≤8%
15%(等级AD)的电流 THD 限值。
3. 测量与改善
测量方法
使用谐波分析仪或真有效值示波器(True-RMS)分别测量 I_1 与各次谐波有效值,代入公式计算。
改善手段
有源滤波器 (APF):在线检测并动态补偿谐波;
被动滤波器:针对特定次谐波设计 L–C 陷波或低通网络;
PFC(功率因数校正)电路:让输入电流更贴近正弦,减少谐波。
通过 THD 指标,工程师可以定量评估和控制谐波对电力系统和用电设备的影响,确保电能质量符合设计和法规要求。
傅里叶变换
要把已有的电压或电流波形 x(t) 分解出第 1、2、3… n 次谐波分量,核心就是利用傅里叶级数(连续情形)或离散傅里叶变换(数字采样后)。下面分别给出这两种常见方法的原理和步骤。
一、连续傅里叶级数分解(理论公式)
假设波形 x(t) 在周期 T 内满足周期延拓,则可表示为
基波(第 1 次谐波)对应 n=1,频率 \omega_0;
第 n 次谐波对应频率 n\omega_0。
各系数通过正交性积分得到:
峰值幅值 (Peak Amplitude) 为 \sqrt{a_n^2 + b_n^2};
RMS 幅值 (RMS Amplitude) 为 \dfrac{\sqrt{a_n^2 + b_n^2}}{\sqrt{2}};
相位 \varphi_n = atan2(b_n, a_n);
则第 n 次谐波波形为
x_n(t) = a_n \cos(n\omega_0 t) + b_n \sin(n\omega_0 t) = \underbrace{\sqrt{a_n^2 + b_n^2}}_{A_n} \sin(n\omega_0 t + \varphi_n).
二、离散傅里叶变换(DFT/FFT)——数字化处理
当你用示波器或数据采集卡对波形以等间隔采样:
其中 N \Delta t = T 为一个周期(或总采样时间)。
计算离散傅里叶变换
X[k] =\sum_{m=0}^{N-1}x[m]\;e^{-j\frac{2\pi}{N}k\,m}, \quad k=0,1,\dots,N-1.对应关系
第 k 点对应频率 f_k=\tfrac{k}{N}f_s,其中 f_s=\tfrac{1}{\Delta t};
如果采样保证整周期内采 N 点,则第 k 点即第 k 次谐波(基波对应 k=1)。
第 n 次谐波对应 k=n;
重要提示: 当 k > N/2 (假设 N 为偶数) 时,对应的频率 f_k > f_s/2 (奈奎斯特频率),这些点是负频率 (k-N) 分量的复共轭镜像(即 |X[k]| = |X[N-k]|),不代表真实的更高次谐波。实际分析中,通常只考虑 k = 0, 1, 2, ..., \lfloor N/2 \rfloor 的点。
幅值与相位(针对重构物理谐波)
A_k = \frac{2}{N}\bigl|X[k]\bigr|,\qquad \varphi_k = \arg X[k].重构(逆离散傅里叶变换 - IDFT)
利用计算出的频谱 X[k],可以通过逆离散傅里叶变换 (IDFT) 精确重构原始采样信号 x[m]:
x[m] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \, e^{j \frac{2\pi}{N} k m}, \quad m = 0, 1, \dots, N-1.这个公式自动包含了所有频率分量(直流、基波、谐波及其镜像)的幅值和相位信息,是精确重构的标准方法。
三、实际操作步骤示例
采样: 用示波器在一个或多个周期上采样。根据奈奎斯特采样定理,采样率必须满足 f_s > 2 f_{\text{max}} ( f_{\text{max}}是关心的最高谐波频率或信号最高频率)。工程实践中,为获得较好的频谱估计精度和波形细节,常取 f_s \ge 10 \times f_{\text{max}}。 (修改:明确理论最低要求 f_s > 2f_{max} 和工程经验值 f_s \ge 10f_{max})
去直流分量: 若关心 AC 部分,可先去除 a_0 或计算出的直流分量 X[0]。
FFT 计算: 调用软件(MATLAB/Python/示波器内置)计算 DFT(通常使用高效的 FFT 算法)求得 X[k]。
提取谐波: 根据上表计算 k=1,2,3,\dots,n 对应的峰值幅值 A_k 和相位 \varphi_k,即为第 1 到第 n 次谐波的参数。注意: n 必须满足 n \times f_0 < f_s / 2 (其中 f_0 是基波频率),否则该次谐波可能因混叠无法被准确测量或属于镜像分量。 (修改:强调使用正确的幅值计算公式,并补充 n 的上限条件)
可视化: 画出各次谐波的频谱图( A_k 或 RMS 值 vs f_k),或用 IDFT 重构公式验证分解正确性(例如,仅叠加前 n 次谐波分量并与原信号比较)。 (修改:提及频谱图,重构方法改为 IDFT)
可以参考可视化网站学习傅里叶变换
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

