Logo

Menu

张彤
张彤
Published on 2025-07-14 / 5 Visits
0
0

17.交流电路中的无源元件

交流电路中的无源元件

Passive Components in AC Circuits

无源元件是那些只能减少施加于它们的电功率，而不能增加电功率的电路器件。

电气和电子电路是由许多不同的元件连接在一起组成一个完整且闭合的电路。任何电路中使用的三种主要的无源元件是：电阻器、电容器和电感器。这三种无源元件有一个共同点，那就是它们都以非常不同的方式限制电流在电路中的流动。

电流在电路中可以以两种方式之一流动。如果电流仅以一个稳定的方向流动，那么它被归类为直流电（DC）。如果电流在两个方向上来回交替变化，那么它被归类为交流电（AC）。虽然无源元件在电路中表现出阻抗，但在交流电路中它们的行为与在直流电路中非常不同。

无源元件消耗电能，因此无法增加或放大施加在它们上的任何电信号的功率，这仅仅是因为它们是“无源”的，因此它们的增益始终小于1。用于电气和电子电路中的无源元件可以以无限多种方式连接，如下所示，其电路的运行取决于这些元件之间不同电气特性的相互作用。

交流电路中的无源元件

Passive Components in AC Circuits

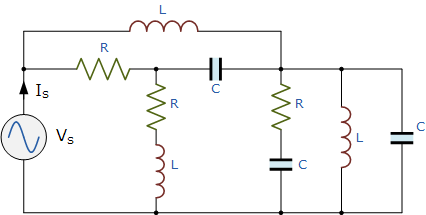
其中： R 表示电阻， C 表示电容， L 表示电感。

无论在直流电路还是交流电路中使用，电阻器的电阻值始终保持不变，与供电频率无关。这是因为电阻器被归类为“纯”元件，具有寄生特性，例如电容 C = \infty 和电感 L = 0。此外，对于纯电阻电路，电压与电流始终同相，因此任意时刻消耗的功率可以通过将该时刻的电压与电流相乘来求得。

而电容器和电感器具有一种不同的交流电阻，称为电抗（ X_L 和 X_C）。电抗同样阻碍电流流动，但电感或电容的电抗并不是像电阻那样具有固定值。电感或电容的电抗值取决于供电电流的频率，以及元件本身的直流参数。

下面列出了交流电路中常用的无源元件及其对应的公式，可用于求取它们的阻抗值或电路中的电流。需要注意的是，理论上“理想”的纯电容器或纯电感器不具有任何电阻，但在真实环境中，无论多么微小，它们总会有一定的电阻值。

纯电阻型无源元件

Purely Resistive Passive Components

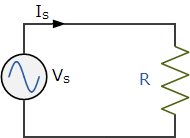
电阻器 —— 电阻器用于调节、阻碍或设定电流通过特定路径的流动，或因电流流动而在电路中产生电压降。电阻器具有一种阻抗，称为电阻（R），其阻值以欧姆（\Omega）为单位。电阻器可以是固定值电阻，也可以是可变电阻（电位器）。

\begin{aligned} Z &= \frac{V_R}{I} = R,\\ Z &= \angle 0^\circ = R + j0,\\ I_S &= \frac{V_S}{R}. \end{aligned}

纯电容型无源元件

Purely Capacitive Passive Components

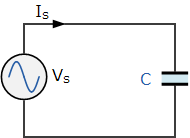
电容器 —— 电容器是一种能够以电荷形式存储能量的元件，类似于一个小型电池，其“容量”即为电容值，单位为法拉（F）。在直流（DC）情况下，电容器表现为开路，具有无限大的阻抗（X_C = \infty）；而在极高频率时，电容器表现为短路，阻抗趋近于零。

\begin{aligned} X_C &= \frac{V_C}{I_C} = \frac{1}{2\pi f C},\\ Z &= \angle -90^\circ = 0 - jX_C,\\ I_S &= \frac{V_S}{X_C}. \end{aligned}

纯电感型无源元件

Purely Inductive Passive Components

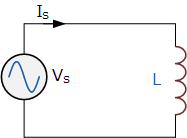
电感器 —— 电感器是由一根或多根绕组导线组成的线圈，当电流通过该线圈时，会在其自身或中心磁芯内产生磁场，从而“感应”出电动势。电感器的电感值以亨利（H）为单位。在直流（DC）情况下，电感器表现为短路，具有零阻抗；而在高频情况下，电感器表现为开路，阻抗趋于无限大（X_L）。

\begin{aligned} X_L &= \frac{V_L}{I_L} = 2\pi f L,\\ Z &= \angle +90^\circ = 0 + jX_L,\\ I_S &= \frac{V_S}{X_L}. \end{aligned}

交流电路中的串联无源元件

Passive Components In Series AC Circuits

交流电路中的无源元件可以串联组合，形成如图所示的 RC、RL 和 LC 电路。

串联 RC 电路

Series RC Circuit

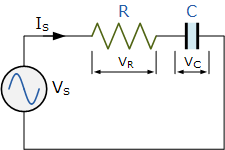
\begin{aligned} Z &= \sqrt{R^2 + X_C^2}, \\ Z &= \angle -\varphi = R - jX_C, \\ \varphi_{( -90^\circ \to 0^\circ )} &= \tan^{-1}\!\Bigl(-\frac{X_C}{R}\Bigr), \\ I_S &= \frac{V_S}{Z} = \frac{V_S}{\sqrt{R^2 + X_C^2}}, \\ V_S &= \sqrt{V_R^2 + V_C^2}. \end{aligned}

串联RL电路

Series RL Circuit

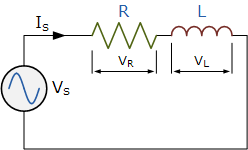
\begin{aligned} Z &= \sqrt{R^2 + X_L^2},\\ Z &= \angle +\varphi = R + jX_L,\\ \varphi_{(0^\circ \to 90^\circ)} &= \tan^{-1}\!\biggl(\frac{X_L}{R}\biggr),\\ I_S &= \frac{V_S}{Z} = \frac{V_S}{\sqrt{R^2 + X_L^2}},\\ V_S &= \sqrt{V_R^2 + V_L^2}. \end{aligned}

串联LC电路

Series LC Circuit

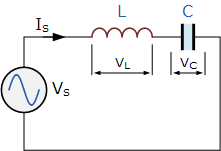
\begin{aligned} Z &= \sqrt{X_L^2 - X_C^2},\\ \therefore Z &= X_L - X_C \quad\text{或}\quad X_C - X_L,\\ Z &= \angle \varphi + j = 0 + (jX_L - jX_C),\\ f_R &= \frac{1}{2\pi\sqrt{L\,C}},\\ \text{在 }f_R:\quad X_L &= X_C,\quad V_L = V_C,\\ I_S &= I_L = I_C. \end{aligned}

交流电路中的并联无源元件

Passive Components In Parallel AC Circuits

交流电路中的无源元件也可以并联组合，形成如下所示的 RC、RL 和 LC 电路。

并联 RC 电路

Parallel RC Circuit

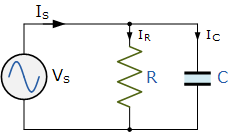
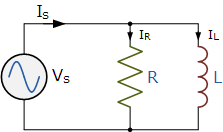
\begin{aligned} I_R &= \frac{V_S}{R}, I_C = \frac{V_S}{X_C}, I_S = \sqrt{I_R^2 + I_C^2},\\ \varphi &= \tan^{-1}\!\bigl(\tfrac{I_C}{I_R}\bigr),\\ Y &= \frac{1}{Z} = \sqrt{G^2 + B_C^2},\\ V_S &= V_R = V_C. \end{aligned}


并联RL电路

Parallel RL Circuit

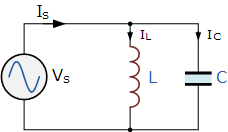
\begin{aligned} I_R &= \frac{V_S}{R}, I_L = \frac{V_S}{X_L}, I_S = \sqrt{I_R^2 + I_L^2},\\ \varphi &= \tan^{-1}\!\Bigl(\frac{I_L}{I_R}\Bigr),\\ Y &= \frac{1}{Z} = \sqrt{G^2 + B_L^2},\\ V_S &= V_R = V_L. \end{aligned}

并联LC电路

Parallel LC Circuit

\begin{aligned} B_L &= \frac{1}{X_L}, B_C = \frac{1}{X_C},\\ Y &= \frac{1}{Z} = -B_L + B_C,\\ f_R &= \frac{1}{2\pi\sqrt{L\,C}},\\ \text{在 }f_R:\quad X_L &= X_C,\quad I_L = I_C,\\ V_S &= V_L = V_C. \end{aligned}

RLC电路中的无源元件

Passive RLC Circuits

在交流电路中，所有三种无源元件也可以组合形成串联 RLC 电路和并联 RLC 电路，如下所示。

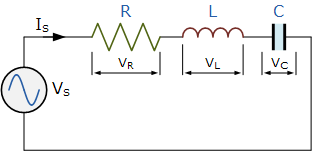
串联RLC电路

Series RLC Circuit

\begin{aligned} Z &= \sqrt{R^2 + (X_L - X_C)^2},\\ Z &= \angle \varphi = R + j\,(X_L - X_C),\\ V_S &= \sqrt{V_R^2 + (V_L - V_C)^2},\\ I_S &= \frac{V_S}{Z} = \frac{V_S}{\sqrt{R^2 + (X_L - X_C)^2}},\\ \varphi &= \tan^{-1}\!\Bigl(\frac{X_L - X_C}{R}\Bigr),\\ I_S &= I_R = I_L = I_C. \end{aligned}

并联RLC电路

Parallel RLC Circuit

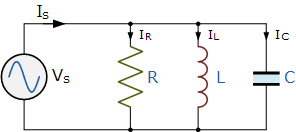
\begin{aligned} G &= \frac{1}{R}, B_L = \frac{1}{X_L}, B_C = \frac{1}{X_C},\\ Y &= \frac{1}{Z} = \sqrt{G^2 + (B_L - B_C)^2},\\ I_S &= \sqrt{I_R^2 + (I_L - I_C)^2},\\ f_R &= \frac{1}{2\pi\sqrt{L\,C}},\\ V_S &= V_R = V_L = V_C. \end{aligned}

如上所示，由于频率（f）的影响，交流电路中无源元件的行为与在直流电路中完全不同。在纯电阻电路中，电流与电压同相；在纯电容电路中，电容器中的电流相对于电压超前 90°；而在纯电感电路中，电流相对于电压滞后 90°。

在交流电路中，阻碍电流流动的量称为：电阻——对于电阻器用 R 表示；容抗——对于电容器用 X_C 表示；感抗——对于电感器用 X_L 表示。电阻与电抗的组合称为“阻抗”。

在串联电路中，各元件上的电压相量之和等于电源电压 V_S；在并联电路中，各支路中电流的相量之和（即各元件中的电流之和）等于电源电流 I_S。

对于串联或并联的 RLC 电路，当电源电流与电源电压“同相”时，即满足 X_L = X_C，电路发生谐振。串联谐振电路称为“受纳电路”（Acceptor Circuit），并联谐振电路称为“拒纳电路”（Rejecter Circuit）。

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途

16.谐波
18.交流电路中的功率

Comment