无功功率
Reactive Power
无功功率最好地描述为交流电路或系统中无功元件reactive components产生的“未使用”功率的量。
这里的active前缀是re不是un,也不是de,说明名字虽然叫无功,只是另有用途而已。
在直流电路中,“伏特 × 安培”(volts × amps)的乘积给出了电路消耗的功率,单位为瓦特(W)。然而,虽然对于纯电阻交流电路这一公式同样成立,但对于包含无功元件的交流电路来说情况就略微复杂一些,因为该伏安乘积会随频率变化,从而影响电路的无功功率。
在交流电路中,电压与电流的乘积以伏安(VA)或千伏安(kVA)表示,称为视在功率Apparent power,符号为 S。在非电感性的纯电阻电路(如加热器、熨斗、电水壶和灯丝灯等)中,其电抗几乎为零,因此电路的阻抗几乎完全由电阻构成。
对于交流纯电阻电路,电流与电压同相 (“in-phase”),任意时刻的功率都可通过该时刻的电压乘以电流来计算;正因为这种“同相”关系,可直接使用有效值(rms)来得到等效直流功率或加热效应。
然而,若电路中包含无功元件,则电压与电流波形会产生由电路相角决定的“相移”(out-of-phase)。当电压与电流之间的相角达到最大值 90^\circ 时,伏安乘积在一个周期内正负值相等。换言之,无功电路将向电源返还与其从电源吸取的能量相同的功率,导致电路的平均功率消耗为零,因为等量的能量在电源与负载之间来回流动。
由于此时虽有电压和电流,但没有功率耗散,表达式 P = I V \quad(\text{rms}),已不再适用,因此可见交流电路中的伏安乘积并不必然等同于电路消耗的实际功率。要确定交流电路消耗的“有功功率”(Active Power,符号 P),不仅要考虑伏安乘积,还需考虑电压与电流波形之间的相角差,其公式为: P = V \, I \cos\Phi,因此,视在功率 S 与有功功率 P 之间的关系可写为:
请注意,功率因数(PF)定义为有功功率(以瓦特为单位)与视在功率(以伏安为单位)之比,用以表明电能的利用效率。在非电感性纯电阻交流电路中,由于 \frac{P}{S}=1,有功功率将等于视在功率。电路的功率因数可以用小数或百分比表示。
然而,除有功功率和视在功率外,每当存在相角时,还会出现另一种功率分量,称为无功功率(有时也称为虚功imaginary power)。它的单位是伏安无功(VAr)volt-amperes reactive,符号为 Q,其计算公式为:
无功功率(或 VAr)并不是真正耗散的功率,而是表示电压与电流相位不同步时的伏安乘积。无功功率用于帮助建立和维持交流电设备所需的电场和磁场。其大小取决于电压与电流之间的相移(相角),且与有功功率一样,无功功率在“供给”supplied时为正值,在“吸收”consumed时为负值。
大多数利用磁场的电气设备(如电动机、发电机和变压器)都需要无功功率,架空输电线路的无功损耗也需由无功功率来补偿。
在交流电路中,有功功率(P,watt)、视在功率( S,VA)和无功功率( Q,VAr)三者的关系可用直角三角形的三条边来表示,这种表示称为“功率三角形”,如下所示:
交流电路中的功率
Power in an AC Circuit
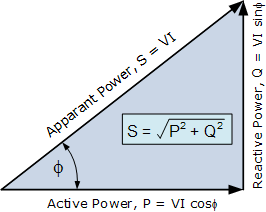
从上述功率三角形我们可以看到,交流电路供应或消耗两种功率:有功功率和无功功率。同时,有功功率永远不会为负,而无功功率则可为正或负值,因此减少无功功率有助于提高系统效率。
使用交流电力配电的主要优势在于可以通过变压器改变供电电压等级,但家用电器、空调和工业设备所用的变压器和感应电动机都会消耗无功功率,这会占用输电线路的容量,因为需使用更粗的导线和更大容量的变压器来承载增大的电流,从而增加费用。
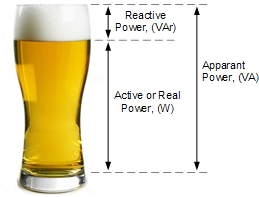
在许多方面,无功功率可被比作一品脱啤酒杯顶端的泡沫。你为一整杯啤酒付费,但真正喝到的液体啤酒通常少于满杯,因为泡沫占用了杯中的空间——无功功率的作用与此类似。
但在许多工业电力应用中,无功功率对电路也是有用的。虽然有功功率是真正用来驱动电动机、取暖或照明的能量,无功功率则承担了调节电压的重要功能,从而帮助电能通过电网和输电线路有效地传输到负载处。
虽然减少无功功率以改善功率因数和系统效率是有益的,但不足的无功功率则无法维持输电网络的电压,使得有功功率无法传送。然而,过多的无功功率又会导致线路中电流增大,造成过量的 I^2R 损耗以及不利的电压降和功率损失。
无功功率的功率因数校正
Power Factor Correction of Reactive Power
一种避免无功功率费用的方法是安装功率因数校正电容器。通常,居民用户仅按消耗的有功功率(千瓦时,kW·h)收费,因为大多数家用和单相负载的功率因数值基本相同——制造商已在大多数家用电器内置了功率因数校正电容器。
而对于使用三相电源的工业用户而言,其功率因数差异很大,因此电力公司可能需要将这些工业用户的功率因数纳入考量:如果功率因数低于规定值,就要对用户收取额外费用。这是因为为工业用户供电成本更高,需要更粗的导线、更大容量的变压器和更大规格的开关设备来承载更大的电流。
通常,功率因数低于 0.95 的负载需要更多的无功功率;功率因数高于 0.95 则被视为良好,因为电能被更有效地利用;而功率因数等于 1.0(或“单位功率因数”)则被视为理想状态,不消耗任何无功功率。
由此可见,“视在功率”是“有功功率”和“无功功率”两者的组合。有功功率仅来自电路中的电阻性元件,而无功功率则来自包含电容或电感元件的电路。几乎所有交流电路都同时包含 R、L、C 三种元件的组合。
由于无功功率会“占用”视在功率中的一部分,因此在电气系统中必须考虑无功功率,以确保所提供的视在功率足以满足负载需求。这是理解交流电源的关键——电源必须能够提供足够的伏安(VA)功率,以驱动任何给定的负载。
附录
无功功率的作用
无功功率虽本身不做实际功(不产生机械能或热能),但它对交流电网和各种电气设备的正常工作却必不可少,原因主要有以下几点:
维持磁场和电场
对于电动机、变压器、同步机等电磁设备来说,其转子或铁芯需要持续的磁场才能工作。无功功率正是用来建立和维持这个磁场能量的载体,没有足够的无功,就无法维持设备的磁通,从而导致电机转不起来、变压器无法正常电压变换。
类似地,输电线路中的电场分布也需要无功功率来维持,否则线路电压会下降,影响长距离输电的能力。
电网电压调节与稳定
无功功率与电网电压成正相关:当无功功率供应不足时,线路末端电压会出现严重下垂,可能导致用电设备无法启动或运行不稳;当无功过剩时,电压又会升高,可能损伤设备或引起过电压保护动作。
因此,电力系统中会通过并联电容器、同步调相机、FACTS 装置等手段,动态地补偿和调节无功,以保持电网电压在安全、经济的范围内。
输电损耗与容量利用
虽然无功本身不做功,但它会在输电线路中产生额外电流,从而引起 I^2R 损耗。如果无功过多,则线路损耗增大;如果无功不足,则电压下垂严重,必须增大线路容量或提高电压等级,成本也会增加。
因此,输电系统必须在“无功过多”和“无功不足”之间取得平衡:既要提供足够的无功以保证电压和设备运行,又要尽量减少无功造成的额外损耗。
等效模型中的必要性
在交流等效电路中,电压源与电流源之间的相位差 \Phi 决定了有功与无功的分量。无功功率 Q=VI\sin\Phi 是系统电压和电流保持正交分量的一种体现,缺少这部分分量,电网模型就不完整,也无法正确描述能量在电网中的传输与分配。
无功功率与线损
无功功率与线路损耗(线损)之间的关系,归根结底是通过“电流”这一中介体现的。下面从原理、定量分析和工程应用三个层面来详细阐述。
一、基本原理
线路损耗(I²R 损耗) 交流输电线路中的铜(或铝)导体具有电阻 R,当线路中流过电流 I 时,就会产生热损耗,其瞬时功率为
P_{\text{loss}}(t) = i^2(t)\,R.取有效值后,平均线损为
P_{\text{loss}} = I^2_{\mathrm{rms}} \, R.视在功率与电流的关系 对于三相平衡交流系统,任一相的电流与相电压 V 和视在功率 S 的关系为
I = \frac{S}{\sqrt{3}\,V}.其中 S = \sqrt{P^2 + Q^2}, P 为有功功率, Q 为无功功率。
无功功率对视在功率的影响 当负载无功需求 Q 增大时,视在功率
S = \sqrt{P^2 + Q^2}随之增大,即使有功功率 P 不变,线路电流 I 也会增加。这就直接导致线损增大。
二、定量分析
假设三相系统中有功负载 P 恒定、线路阻抗 R 恒定,考虑两种功率因数情况:
功率因数为 1(纯电阻负载)
Q = 0,\quad S_1 = P,\quad I_1 = \frac{P}{\sqrt{3}V}.此时线损为
P_{\text{loss,1}} = I_1^2\,R = \Bigl(\frac{P}{\sqrt{3}V}\Bigr)^2 R.功率因数为 \cos\varphi < 1
Q = P\tan\varphi,\quad S_2 = \sqrt{P^2 + (P\tan\varphi)^2} = \frac{P}{\cos\varphi},\quad I_2 = \frac{P}{\sqrt{3}V\,\cos\varphi}.此时线损为
P_{\text{loss,2}} = I_2^2\,R = \Bigl(\frac{P}{\sqrt{3}V\,\cos\varphi}\Bigr)^2 R = \frac{1}{\cos^2\varphi}\;\Bigl(\frac{P}{\sqrt{3}V}\Bigr)^2 R = \frac{P_{\text{loss,1}}}{\cos^2\varphi}.
由此可见,当功率因数 \cos\varphi 下降时,线损按 \frac{1}{\cos^2\varphi} 放大。例如,若 \cos\varphi=0.8,线损就增大至原来的 \tfrac{1}{0.8^2}=1.5625 倍。
三、工程应用
无功补偿(功率因数校正)
在用户侧或配电网侧安装电容器组(或同步调相机/STATCOM 等),提供所需的无功功率 Q_C,使得系统中流过输电线路的无功功率需求降为零或降到可接受水平。
补偿后,残余视在功率 S' = \sqrt{P^2 + (Q - Q_C)^2} 减小,从而电流 I' 和线损 P'_{\text{loss}} 也随之降低。
无功分布与分级补偿
集中补偿(电厂/配电变电所):适用于大范围的无功需求调节,减少长距离输电的无功流动。
分布补偿(负载侧):在大的工业负载或楼宇端直接补偿,可显著降低末端配电线路的电流与损耗。
动态无功调节
采用 SVC(静止无功补偿器)、STATCOM 等 FACTS 装置,根据电网运行状态动态调节无功注入或吸收,实时优化功率因数,进一步降低线损并改善电压质量。
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

