并联谐振电路
Parallel Resonance Circuit
并联谐振发生在电源频率使电源电压与电流之间的相位差为零时,使电路呈现纯阻性。
在许多方面,并联谐振电路与我们在前一教程中研究的串联谐振电路完全相同。它们都是包含两个无功元件的三元件网络,使电路成为二阶电路;两者都受电源频率变化的影响,并且都存在一个频率点,在该点上它们的两个无功分量相互抵消,从而影响电路特性。两种电路都具有谐振频率。
然而,这一次的不同之处在于,并联谐振电路受到并联 LC 谐振腔内各支路电流的影响。谐振腔(tank 电路)是 L 和 C 的并联组合,用于滤波网络中选择或抑制交流频率。请看下图所示的并联 RLC 电路。
并联 RLC 电路
Parallel RLC Circuit

让我们来定义一下我们已知的关于并联 RLC 电路的内容:
包含电阻 R、电感 L 和电容 C 的并联电路,当并联组合的结果电流与电源电压同相时,就产生了并联谐振parallel resonance(也称“反谐振”anti-resonance)。在谐振时,由于振荡能量会在电感和电容之间不断往返传递,会在它们之间产生很大的环流circulating current,从而使并联电路出现电流谐振current resonance。
并联谐振电路将电路能量储存在电感的磁场和电容的电场中,这些能量来回转换,使得从电源抽取的瞬时电流和能量总和为零。
这是因为电感电流 I_L 与电容电流 I_C 的瞬时值始终大小相等、方向相反,故从电源吸取的电流为这两者与电阻支路电流 I_R 的矢量和。
在交流并联谐振电路的分析中,电源电压对所有支路都是共用的,可视为参考矢量。每个并联支路必须分别计算电流,然后再做矢量相加;或者先计算各支路的导纳,再由总导纳求出总电流。
我们已知在前一教程中,当电感电压 V_L 与电容电压 V_C 大小相等而方向相反(即 X_L=X_C)时,就发生了谐振。并联电路的总导纳可表示为:
当 X_L = X_C 且导纳 Y 的虚部为零时,发生谐振。即:
请注意,在谐振时,并联电路得到的方程与串联谐振电路完全相同。因此,无论电感或电容是并联还是串联连接,都没有区别。
同样,在谐振时,并联 LC 谐振腔表现为开路,电路电流仅由电阻 R 决定。因此,并联谐振电路在谐振时的总阻抗仅等于电路中的电阻值,即 Z = R。
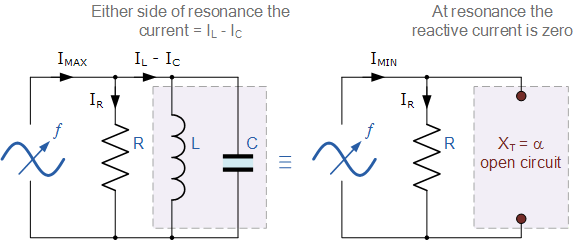
并联谐振电路中的阻抗
Impedance in a Parallel Resonance Circuit
因此,在谐振时,并联电路的阻抗达到最大值,且等于电路中的电阻值,从而使电路呈现高阻抗、低电流的状态。同样在谐振时,由于电路的阻抗仅为电阻,电路总电流 I 将与电源电压 V_S 同相。
我们可以通过改变该电阻的数值来调节电路的频率响应。在电感 L 和电容 C 保持不变的情况下,改变 R 的数值会影响电路在谐振时的电流大小。此时电路在谐振频率下的阻抗 Z = R_{\max},被称为电路的“动态阻抗”。
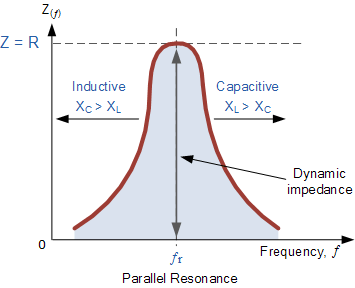
请注意,当并联电路在谐振时阻抗达到最大值,其导纳必然达到最小值。并联谐振电路的一个特性就是导纳很低,从而限制电路电流。与串联谐振电路不同,并联谐振电路中的电阻对电路带宽具有阻尼作用,使电路选择性降低。
无阻尼理想情况 若并联电路中只有理想的 L 和 C,没有任何能量损耗,谐振曲线会非常尖锐——在共振点外,电路几乎不响应其他频率,选择性极高,对频率的区分能力也极强,相当于质量因数 Q\to\infty。
加入电阻后的阻尼 并联支路中并联了电阻 R,相当于在每个振荡周期中,电路都会有一部分能量以热的形式被耗散。能量的耗散使得谐振峰变得不再那么尖锐,出现了一个有限的“半功率带宽”(-3\rm dB 带宽),从而降低了对频率的选择性。这种因耗散而导致的峰值变宽的现象,就称为“阻尼”。
此外,由于电路总电流对于任意阻抗 Z 都保持不变,并联谐振电路两端的电压波形与总阻抗的变化形状相同;对于并联电路,电压波形通常取自电容两端。
现在我们知道,在谐振频率 f_r 处,电路导纳达到最小值,且等于电导 G,即 G = \frac{1}{R},因为在并联谐振电路中,导纳的虚部(纳抗) B 为零,即 B_L = B_C:
谐振电路的导纳
Susceptance at Resonance
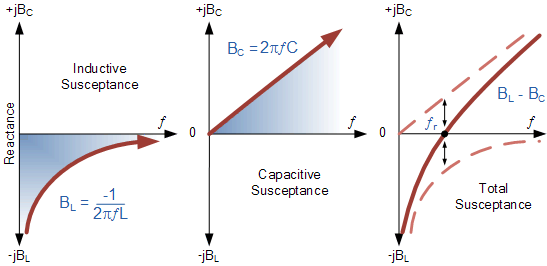
如上所述,感性纳抗 B_L 与频率成反比,用双曲线表示;容性纳抗 B_C 与频率成正比,用直线表示。最终曲线描绘了并联谐振电路的总纳抗随频率的变化,该曲线即两者之差:
在谐振频率处,总纳抗曲线与横轴相交,总纳抗为零。
在谐振频率以下,感性纳抗占优势,电路表现为“滞后”功率因数;
在谐振频率以上,容性纳抗占优势,电路表现为“超前”功率因数。
因此,在谐振频率 f_r 时,并联电路中只有电阻承担电流,从电源抽取的电流必与电压同相,功率因数为一( \theta=0^\circ)。
此外,由于并联电路的阻抗随频率变化,电路阻抗具有“动态”特性;在谐振时,电路阻抗等于纯电阻,所对应的电流与电压同相。我们已经看到,并联谐振电路在谐振时的阻抗等同于电阻值,该值即为电路的最大动态阻抗 Z_d。
并联谐振电路中的电流
Current in a Parallel Resonance Circuit
由于在谐振频率处总纳抗为零,导纳达到最小值,且等于电导 G。因此在谐振时,流经电路的电流也达到最小值,因为电感支路电流 I_L 与电容支路电流 I_C 大小相等( I_L = I_C),且相位相差 180^\circ。
我们记得,并联 RLC 电路中总电流等于各支路电流的矢量和,对于给定频率,其计算公式为:
并联谐振电路中的电流
由于在谐振频率处总纳抗为零,导纳达到最小值,且等于电导 G。因此在谐振时,流经电路的电流也达到最小值,因为电感支路电流 I_L 与电容支路电流 I_C 大小相等(I_L = I_C),且相位相差 180^\circ。
我们知道,在并联 RLC 电路中,总电流等于各支路电流的矢量和。对于给定频率,其计算公式为:
在谐振时,电感支路电流 (I_L) 与电容支路电流 (I_C) 大小相等且方向相反,相互抵消,使得净无功电流为零。 此时,以上公式变为:
由于流经并联谐振电路的电流等于电压除以阻抗,因此在谐振时阻抗 Z 达到最大值(即 Z = R)。 因此,该频率下的电路电流将达到最小值: I = \frac{V}{Z} = \frac{V}{R}
并联谐振电路的电流–频率特性曲线如下(横轴为频率 f,纵轴为电流 I):
并联谐振电路中的电流
Parallel Circuit Current at Resonance
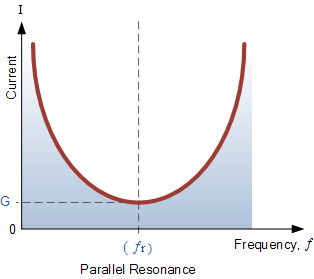
并联谐振电路的频率响应曲线表明,电流的幅值是频率的函数。将其绘制在图上可见:响应在最低频率时从最大值开始,随着频率升高逐渐减小,在谐振频率处达到最小值,此时I_{\min} = I_R,然后随着频率继续增大,电流又重新上升,当 f\to\infty 时再次趋向最大值。
由此可见,通过电感 L 与电容 C 组成的谐振腔流过的电流幅值,即使在谐振点,也可能比电源电流大数倍;但由于它们大小相等且相位相反(相差 180^\circ),因此在总电流中相互抵消。
因为并联谐振电路只在谐振频率附近起作用,所以这种电路也称为“陷波电路”(Rejecter Circuit)。在谐振时,电路阻抗达到最大值,从而抑制或“拒绝”与其谐振频率相同的电流。并联电路的这种谐振效应也称为“电流谐振”。
上述用于描述并联谐振电路的计算与图形,与我们在串联电路中使用的几乎相同。但并联电路的特性与曲线却与串联电路完全相反:并联电路的最大/最小阻抗、电流及增益位置都与串联电路颠倒。这也是并联谐振电路又称反谐振电路(Anti-resonance Circuit)的原因。
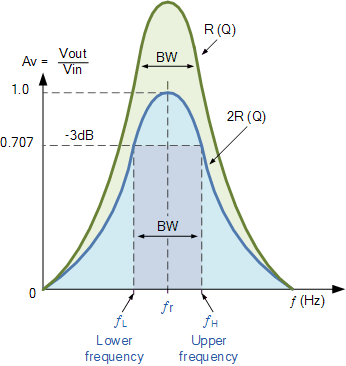
并联谐振电路的带宽与选择性
并联谐振电路的带宽定义方式与串联谐振电路完全相同。上截止频率 f_{\text{upper}} 和下截止频率 f_{\text{lower}} 分别表示电路中功率衰减到谐振频率时总功率一半处的频率,即
对应电流值为其最大谐振电流的 70.7%,即
也就是典型的 –3 dB 点。
与串联电路相同,在谐振频率 f_r 保持不变的情况下,品质因数 Q 增大时带宽会减小;反之, Q 减小时带宽会增大。带宽定义为:
此外,通过改变电感 L 与电容 C 的比值,或改变电阻 R 的数值,都可以在谐振频率固定的情况下调整电路的带宽及频率响应。这一技术被广泛应用于无线电和电视发射机及接收机的调谐电路中。
并联谐振电路的选择性(或品质因数 Q-factor)通常定义为环路支路电流与电源电流的比值,表示为:
请注意,并联谐振电路的品质因数表达式恰好是串联谐振电路中品质因数表达式的倒数。此外,在串联谐振电路中,品质因数反映的是电路的电压增益;而在并联谐振电路中,品质因数则反映电路的电流增益。
并联谐振电路的带宽
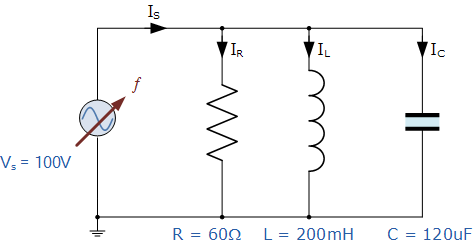
并联谐振电路示例1
一个由 60Ω 电阻、120 μF 电容和 200 mH 电感组成的并联谐振网络,连接在一个对所有频率均输出恒定 100 V 的正弦电压源上。计算:
谐振频率
电路的品质因数
电路的带宽
谐振时的电路电流
电流放大倍数
谐振频率 f_r
f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{0.2 \times 120\times10^{-6}}} \approx 32.5\ \mathrm{Hz},\\谐振时的电感电抗 X_L
X_L = 2\pi f_r L = 2\pi \times 32.5 \times 0.2 \approx 40.8\ \Omega,\\品质因数 Q
Q = \frac{R}{X_L} = \frac{60}{40.8} \approx 1.47,\\带宽 \mathrm{BW}
\mathrm{BW} = \frac{f_r}{Q} = \frac{32.5}{1.47} \approx 22\ \mathrm{Hz},\\上、下 –3 dB 频率点 f_H 和 f_L
f_L = f_r - \frac{\mathrm{BW}}{2} = 32.5 - \frac{22}{2} = 21.5\ \mathrm{Hz},\\ f_H = f_r + \frac{\mathrm{BW}}{2} = 32.5 + \frac{22}{2} = 43.5\ \mathrm{Hz},\\谐振时的电路电流 I_T
在谐振时,电路的动态阻抗等于 R。
I_T = I_R = \frac{V}{R} = \frac{100}{60} \approx 1.67\ \mathrm{A},\\电流放大倍数 I_{\mathrm{mag}}
I_{\mathrm{mag}} = Q\,I_T = 1.47 \times 1.67 \approx 2.45\ \mathrm{A},\\注意:在谐振时,从电源吸取的电流(即电阻支路电流)仅为 1.67 A,而流经 LC 谐振腔的电流则更大,达到 2.45 A。我们可以通过计算谐振时电感(或电容)支路中的电流来验证该数值。
并联谐振教程总结
我们已经看到,并联谐振电路与串联谐振电路非常相似。当两个无功元件相互抵消,使电路总电流与电源电压“同相”时,便发生并联谐振。
导纳与电流最小 在谐振时,电路的导纳达到最小值,且等于电路的电导;同时,从电源抽取的电流也达到最小值,其大小仅由并联电阻决定。
谐振频率公式相同,但元件影响不同 计算谐振频率点所用的公式与串联电路完全相同。然而,在串联 RLC 电路中,无论电感、电容是纯元件还是含损耗元件,都不会改变谐振频率的计算;而在并联 RLC 电路中,含有内阻的电感会影响谐振频率。
纯元件假设与实际差异 本教程中,我们假设电感和电容均为纯无损元件(零电阻或零电纳)。但实际上,电感器(包括螺线管)是由铜线绕制而成,其绕组中总会存在一定的串联电阻 R_S。
因此,上述用于计算纯并联谐振电路谐振频率 f_r 的基本公式,需要稍作修正,以考虑电感器的串联电阻。
含串联电阻电感时的谐振频率
(下一节将给出修正后的公式及推导)
附录
反谐振电路
为什么叫做振荡电路
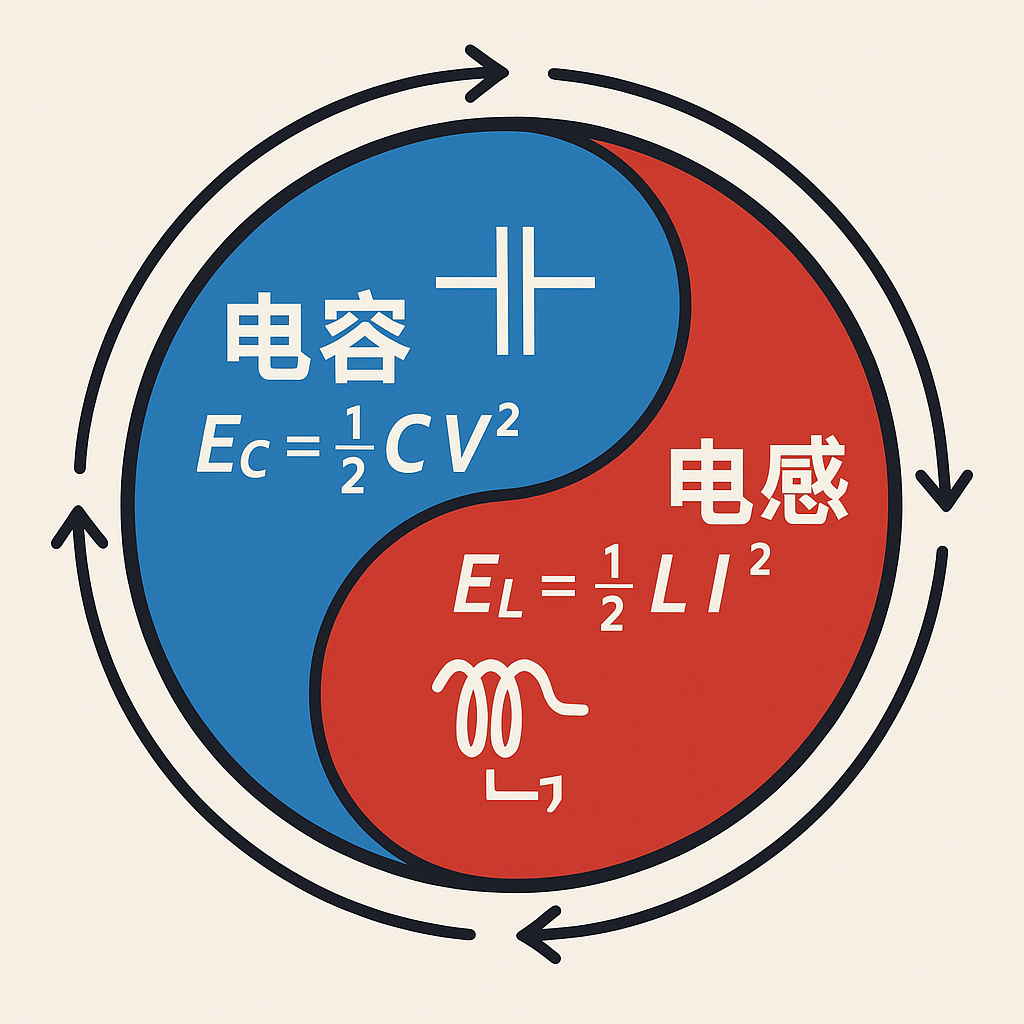
LC 电路中的电容器和电感器都是能量的“存储元件”,它们以不同的形式交替存储和释放能量:
电容器储能
E_C = \tfrac12\,C\,V^2当电容两端电压达到最大时,电容中储存的电能最多,此时电路电流为零。
电感器储能
E_L = \tfrac12\,L\,I^2当电路电流达到最大时,电感中储存的磁能最多,此时电容两端电压为零。
能量转换过程
初始:电容器以电场形式储能,电感电流为零。
电容放电:电容释放能量,电流加速流经电感,电感开始储存能量于磁场。
电感放能:电感磁能又通过电流补充回电容,使电容两端产生相反极性的电压。
周而复始:在理想无损耗情况下,这一过程不断往复,形成电能与磁能之间的谐振振荡。
因此,电容与电感交替地、相互转换地存储和释放能量。 capacitor-to-inductor-to-capacitor 的能量流动,正是谐振电路能够“振荡”起来的本质所在。最后放出振荡太极图。
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

