串联谐振电路
当电源频率使电感 L 和电容 C 两端的电压幅值相等且相位相反时,就会发生谐振。
谐振电路由电阻 R、电感 L 和电容 C 元件组成,其频率响应特性会随着频率的变化而改变。在本教程中,我们将研究串联谐振电路的频率响应,并学习如何计算其谐振频率resonant 和截止频率cut-off frequencies。
到目前为止,我们已经分析了在固定频率稳态正弦电源驱动下,串联 RLC 电路的行为。在有关串联 RLC 电路的教程中,我们也了解到,只要多个正弦信号具有相同的供电频率,就可以使用相量将它们组合起来。
但是,如果向电路施加一个幅值固定但频率可变的电压源,电路的特性会发生怎样的变化?当频率改变时,两个无功元件的“频率响应”行为又会如何?
在串联 RLC 电路中,当电感感抗与电容容抗相等时,即 X_L = X_C,此时的频率点称为电路的谐振频率( f_r),对于串联 RLC 电路,这种谐振称为串联谐振。
串联谐振电路是电气和电子电路中最重要的电路之一。它们可用于交流电源滤波器、噪声滤波器,以及无线电和电视调谐电路中,形成对不同频率通道的高度选择性调谐。请看下图所示的简单串联 RLC 电路示意图:
串联 RLC 电路
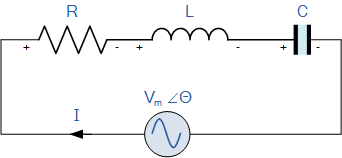
首先,我们重温一下串联RLC电路:
从上述电感感抗公式可见,如果频率或电感量增加,则电感器的感抗值也会增加。当频率趋于无穷大时,电感的感抗也会趋于无穷大,电路元件表现得像一个开路open circuit。
然而,当频率趋近于零或直流时,电感的感抗会减小到零,产生相反的效果,表现得像一个短路short circuit。这意味着感抗与频率“成正比”Proportional,在低频时较小,而在高频时较大,如下曲线所示:
感抗频率
Inductive Reactance against Frequency
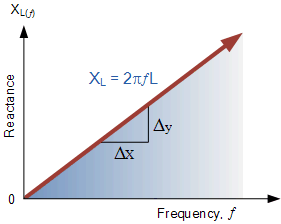
感抗与频率的关系图是一条直线。电感器的感抗值随着频率的增加而线性增加。因此,感抗为正,并且与频率成正比( X_L∝f)。
上述容抗公式同样适用,但情况相反。如果频率或电容增大,则总容抗会减小。当频率趋于无穷大时,电容的容抗几乎降为零,使电路元件表现得像零欧姆的完美导体。
但是,当频率趋近于零或直流时,电容的容抗会迅速增大到无穷大,使其表现得像一个非常大的电阻,更像是开路。由此可见,对于任何给定的电容值,容抗与频率成“反比”Inversely proportional,如下所示:
容抗频率
Capacitive Reactance against Frequency
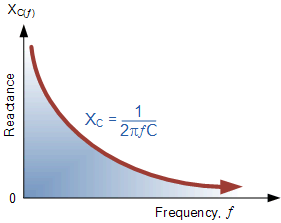
电容感抗随频率变化的曲线是一条双曲线。在低频时,电容的感抗值非常大,但随着施加在其上的频率增加,感抗值迅速减小。因此,容抗具有负值并且与频率成反比(X_C \propto f^{-1})。
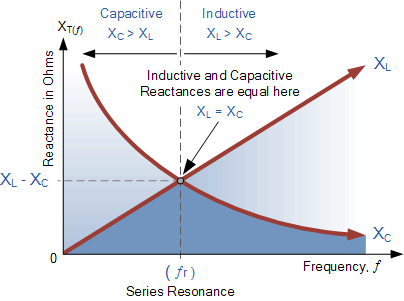
我们可以看到,这些阻抗的数值取决于电源的频率。在高频时, X_L 很大;在低频时, X_C 很大。因此,必然存在一个频率点,在该点上 X_L 的数值与 X_C 的数值相同。
如果我们将电感感抗曲线叠加到电容感抗曲线上,使两条曲线共用同一坐标轴,则它们的交点即为串联谐振频率点(f_r 或 \omega_r),如下所示:
谐振频率
Series Resonance Frequency
其中: f_r 的单位是赫兹, L 的单位是亨利, C 的单位是法拉。
当电路中两种感抗相反且相等时,即 X_L = X_C,在交流电路中就会发生电气谐振。上述图中,这一情形对应于两条感抗曲线的交点。
在串联谐振电路中,谐振频率 f_r 可以按如下方式计算:
我们可以看到,在谐振时,数学上两种电抗相互抵消,即 X_L - X_C = 0,这使得串联的 L–C 组合表现为短路,在串联谐振电路中对电流的唯一阻碍就是电阻 R。
用复数形式表示,谐振频率就是使串联 RLC 电路的总阻抗变为纯“实数”分量的频率——此时不存在任何虚部阻抗,因为它们已被互相抵消。因此,串联电路的总阻抗仅为电阻值,即 Z = R。
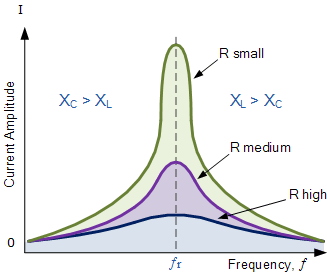
在谐振点,电路阻抗达到最小值,仅等于电路的电阻 ( R)。此时的电路阻抗称为“动态阻抗”。在谐振两侧,根据频率的不同,高频时容性电抗 ( X_C) 占优,低频时感性电抗 ( X_L) 占优,如下图所示。
串联谐振电路中的阻抗
Impedance in a Series Resonance Circuit
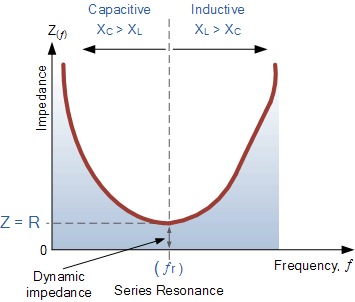
请注意,当容抗主导电路时,阻抗曲线呈双曲线形;而当感抗主导电路时,由于感抗对频率的线性响应,曲线则表现出非对称特性non-symmetrical。
你也会发现,当电路在谐振点阻抗达到最小时,导纳就达到最大值;而串联谐振电路的一个显著特征就是其导纳很高。但这可能带来不利影响——谐振时极低的电阻会导致电路中的电流可能异常增大,存在危险。
回顾之前关于串联 RLC 电路的教程,串联组合的电压是 V_R、V_L 和 V_C 的相量和。
因此,当两种电抗在谐振时相等并互相抵消时,表示 V_L 和 V_C 的两种电压相量也大小相等、方向相反,从而相互抵消(在纯元件情况下,它们分别相位 +90° 和 –90°)。
于是,在串联谐振电路中,由于 V_L = -V_C,反应性电压总和为零,所有电源电压都加在电阻 R 上,即 V_R = V_{\text{supply}}。也正因为如此,串联谐振电路被称为“电压谐振电路”(与之对应的并联谐振电路则是“电流谐振电路”)。
谐振时的串联 RLC 电路
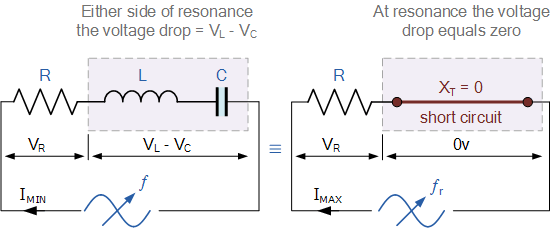
由于流过串联谐振电路的电流等于电压除以阻抗,在谐振时,阻抗 Z 达到最小值(Z = R)。因此,在此频率下,电路电流将达到最大值 \displaystyle \frac{V}{R},如图所示。
谐振时的串联电路电流
Series Circuit Current at Resonance
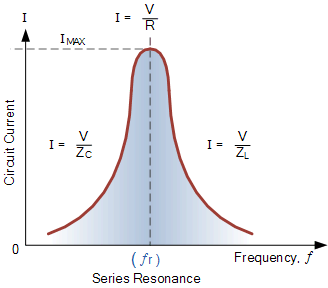
串联谐振电路的频率响应曲线表明,电流的幅值是频率的函数。将其绘制在坐标图上可见,响应在接近零处开始,在谐振频率处达到最大值(I_{\max}=I_R),然后随着 f\to\infty 再次下降到接近零。
其结果是,即使在谐振时,电感 L 和电容 C 两端的电压幅值也可能远大于电源电压,但由于它们大小相等且相位相反,会相互抵消。
由于串联谐振电路仅在谐振频率下起作用,这种电路也称为“接受器电路”(Acceptor Circuit),因为在谐振时电路阻抗达到最小,从而最容易接受频率等于其谐振频率的电流。
你还会注意到,谐振时电路中的最大电流仅受电阻 R(一个实部数值)限制,因此在此频率下,电源电压与电路电流必然同相。
因此,对于固定的电源电压,串联谐振电路中电压与电流之间的相位角也是频率的函数;在谐振频率点,相位角为零,此时 V、I 和 V_R 完全同相。由此可见,当相位角为零时,功率因数power factor必为 1。
串联谐振电路的相位角
Phase Angle of a Series Resonance Circuit
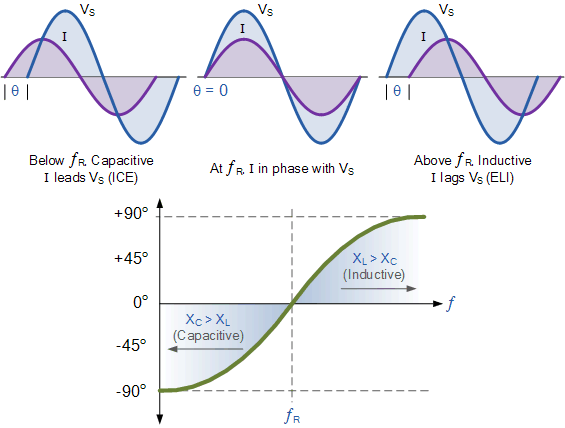
还要注意,相位角在高于谐振频率 f_r 的频率时为正,在低于 f_r的频率时为负,这可以通过以下方法证明:
串联谐振电路的带宽
Bandwidth of a Series Resonance Circuit
如果用恒定电压驱动串联 RLC 电路并改变频率,那么电流幅值 I 与阻抗 Z 成正比,因此在谐振时,电路吸收的功率
将达到最大值。
如果我们降低或提高频率,直到串联谐振电路中电阻吸收的平均功率是谐振时最大值的一半,就会产生两个频率点,称为半功率点(half-power points),相对于最大值而言下降了 3 dB(以 0 dB 为最大电流参考)。
这两个 –3 dB 点对应的电流值是谐振时最大电流的 70.7%,其定义为:
其中,功率降至一半时对应的低频点称为“下截止频率”(f_L),相应的高频点称为“上截止频率”(f_H)。
这两个频率点之间的差值( f_H - f_L)称为带宽(Bandwidth,BW),即电路至少能提供一半最大功率和电流的频率范围,如下图所示。
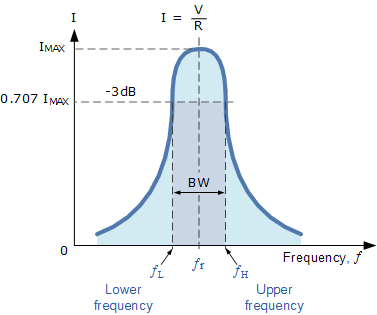
电路电流幅值的频率响应与串联谐振电路中谐振峰的“尖锐度”有关。峰值的尖锐度可以定量衡量,称为电路的品质因数 Q。
品质因数将电路中储存的最大或峰值能量(由电抗决定)与每个振荡周期中消耗的能量(由电阻决定)进行比较,这意味着它等于谐振频率与带宽的比值,电路的 Q 值越高,带宽越窄,即
由于带宽取自两个 –3 dB 点之间,电路的选择性(selectivity )即衡量其拒绝这两个频率点两侧信号的能力。选择性越高,带宽越窄;选择性越差,带宽越宽。
串联谐振电路的选择性可仅通过调节电阻值来控制,其他元件保持不变,因为
串联 RLC 谐振电路的带宽(Bandwidth)就是上下 –3 dB 点之间的频率范围。
串联RLC谐振电路的带宽
接下来,对于串联谐振电路,谐振频率、带宽、选择性和品质因数之间的关系定义为:
谐振频率
Resonant Frequency( f_r)\begin{aligned} X_L &= X_C \;\Longrightarrow\; \omega L - \frac{1}{\omega C} = 0,\\ \omega_r^2 &= \frac{1}{LC} \;\therefore\; \omega_r = \frac{1}{\sqrt{LC}}. \end{aligned}电流
Current( I)\text{在 }\omega = \omega_r\text{ 时,}Z_T = \min,\quad I_s = \max。I_{\max} = \frac{V_{\max}}{Z} = \frac{V_{\max}}{\sqrt{R^2 + \bigl(X_L - X_C\bigr)^2}} = \frac{V_{\max}}{\sqrt{R^2 + \displaystyle\bigl(\omega L - \tfrac{1}{\omega C}\bigr)^2}}下截止频率
Lower cut-off frequency( f_L)\begin{aligned} &\text{在半功率点 } \frac{P_{\mathrm{m}}}{2}\text{ 时,} I = \frac{I_{\mathrm{m}}}{\sqrt{2}} = 0.707\,I_{\mathrm{m}};\\ &Z = \sqrt{2}\,R,\quad X = -R\;(\text{容性});\\ &\omega_L = -\frac{R}{2L} + \sqrt{\left(\frac{R}{2L}\right)^2 + \frac{1}{LC}}。 \end{aligned}上截止频率
Upper cut-off frequency( f_H)\begin{aligned} \text{At half power, } \frac{P_m}{2},\quad I &= \frac{I_m}{\sqrt{2}} = 0.707\,I_m,\\ Z &= \sqrt{2}\,R,\quad X = +R\;(\text{感性}),\\ \omega_H &= +\frac{R}{2L} + \sqrt{\left(\frac{R}{2L}\right)^2 + \frac{1}{LC}}. \end{aligned}带宽
Bandwidth(BW)\mathrm{BW} = \frac{f_r}{Q},\quad f_H - f_L,\quad \frac{R}{L}\ (\mathrm{rads})\ \text{or}\ \frac{R}{2\pi L}\ (\mathrm{Hz})品质因数
Quality Factor(Q)Q = \frac{\omega_r L}{R} = \frac{X_L}{R} = \frac{1}{\omega_r C R} = \frac{X_C}{R} = \frac{1}{R}\sqrt{\frac{L}{C}}
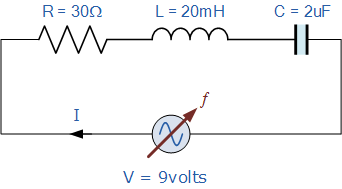
串联谐振电路示例1
一个串联谐振网络由一个 30 Ω 的电阻、一个 2 μF 的电容和一个 20 mH 的电感组成,并连接在一台在所有频率下输出恒定 9 V 的正弦电压电源上。
请计算该电路的:
谐振频率
谐振时的电流
谐振时电感和电容两端的电压
品质因数
带宽
并绘出该电路在所有频率下对应的电流幅值变化曲线。
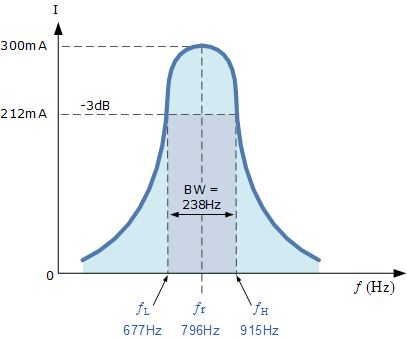
谐振频率 f_r
f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{0.02\times2\times10^{-6}}} \approx 796\ \mathrm{Hz}谐振时的电路电流 I_m
I_m = \frac{V}{R} = \frac{9}{30} = 0.3\ \mathrm{A} = 300\ \mathrm{mA}谐振时的电感感抗 X_L
X_L = 2\pi f L = 2\pi \times 796 \times 0.02 = 100\,\Omega电感和电容两端的电压 V_L,\,V_C
\begin{aligned} V_L &= V_C,\\ V_L &= I \times X_L = 300\,\mathrm{mA} \times 100\,\Omega,\\ V_L &= 30\,\mathrm{volts}. \end{aligned}注意:虽然电源电压仅为 9 伏,但在谐振时,电容两端电压 V_C 和电感两端电压 V_L 可达 30 伏峰值!
品质因数 Q
Q = \frac{X_L}{R} = \frac{100}{30} = 3.33带宽 BW
\mathrm{BW} = \frac{f_r}{Q} = \frac{796}{3.33} = 238\ \mathrm{Hz}上、下 –3 dB 截止频率点 f_H 与 f_L
\begin{aligned} f_L &= f_r - \tfrac{1}{2}\,\mathrm{BW} = 796 - \tfrac{1}{2}(238) = 677\ \mathrm{Hz},\\ f_H &= f_r + \tfrac{1}{2}\,\mathrm{BW} = 796 + \tfrac{1}{2}(238) = 915\ \mathrm{Hz}. \end{aligned}电流波形
串联谐振电路示例2
一个串联电路由一个 4 Ω 的电阻、一个 500 mH 的电感和一个可变电容组成,并连接在 100 V、50 Hz 的电源上。
计算:
为产生串联谐振条件所需的电容值;
在谐振点时,电感和电容两端产生的电压。
谐振频率 f_r:
在谐振时:
因此:
电感和电容两端的电压, V_L,V_C:
总结
在本教程对串联谐振电路进行分析时,你可能已经注意到我们研究了带宽、上/下截止频率、–3 dB 点以及品质因数(Q 因数)。所有这些术语都用于带通滤波器(BPF)的设计与构建;事实上,谐振电路还常用于三元件市电滤波器设计中,用以在“通带”范围内选择性地通过所需频率,同时抑制其他频率。
然而,本教程的主要目标是分析并理解无源串联 RLC 电路中谐振发生的原理。它们在 RLC 滤波网络和滤波器设计中的应用超出了本教程的范围,因此不在此展开,敬请谅解。
要使电路发生谐振,电路中必须至少包含一个电感与一个电容。
谐振是由于电感与电容之间存储的能量在振荡过程中相互转换而产生的。
当 X_L = X_C 且传递函数的虚部为零时,即发生谐振。
在谐振点,电路总阻抗等于电阻值—— Z = R。
在低频时,串联电路呈容性(X_C > X_L),此时功率因数超前。
在高频时,串联电路呈感性(X_L > X_C),此时功率因数滞后。
谐振时电流最大,因而电感与电容两端会产生非常高的电压。
串联谐振电路可用于构建高度频率选择性的滤波器,但其高电流和高元件电压可能对电路造成损害。
谐振电路频率响应最显著的特征是在幅频特性中出现的尖锐谐振峰。
由于谐振时阻抗最小、电流最大,串联谐振电路也称为“接受器电路”(Acceptor Circuit)。
在下一教程“并联谐振”中,我们将研究频率如何影响并联 RLC 电路的特性,以及并联谐振电路的 Q 因数如何决定其电流放大特性。
附录
功率因数计算
功率因数(Power Factor,PF)反映电路中有功功率与视在功率的比值,其计算方式有以下几种常用表达:
定义式
\text{PF} = \frac{\text{有功功率}\;P}{\text{视在功率}\;S} = \frac{P}{V_{\rm rms}I_{\rm rms}}其中
P = V_{\rm rms}I_{\rm rms}\cos\varphi(瓦特,W)
S = V_{\rm rms}I_{\rm rms}(伏安,VA)
\varphi 为电压与电流之间的相位差
代入可得:
\text{PF} = \cos\varphi由阻抗求功率因数
对于串联 RLC 电路,总阻抗为
Z = R + j(X_L - X_C)相位角
\varphi = \arctan\frac{X_L - X_C}{R}因此
\text{PF} = \cos\varphi = \frac{R}{\sqrt{R^2 + (X_L - X_C)^2}} = \frac{R}{|Z|}谐振点特例
在谐振时有 X_L = X_C,则 \varphi=0,\displaystyle\text{PF}=\cos0=1,即“功率因数为 1”。
关于分贝
一、分贝(dB)的概念
分贝(decibel,缩写 dB)是用来表示两个相同物理量(通常是功率或幅度)之比的对数量度,属于“相对值”而非绝对值。
“贝”(Bel, B)最初由 Alexander Graham Bell 的姓氏命名, 1 B = 10 dB。
分贝本身是无量纲的,因为它表示两个同量纲数值的比值的对数。
二、功率比与幅度比的计算
功率比
L_{P}\ (\mathrm{dB}) = 10 \log_{10}\frac{P}{P_{\rm ref}}当 \frac{P}{P_{\rm ref}}=0.5 时,
L_P = 10\log_{10}(0.5)\approx -3.01\ \mathrm{dB}这就是“半功率”对应的 –3 dB。
幅度比(电压或电流)
L_{V}\ (\mathrm{dB}) = 20 \log_{10}\frac{V}{V_{\rm ref}}, \quad L_{I}\ (\mathrm{dB}) = 20 \log_{10}\frac{I}{I_{\rm ref}}当幅度比 \frac{V}{V_{\rm ref}}=0.707 时,
L_V = 20\log_{10}(0.707)\approx -3.01\ \mathrm{dB}.
三、分贝是一种对数比值运算
压缩动态范围
直接用线性刻度(例如伏特、瓦特)时,数值范围可能很大;对数运算能把几十甚至上百倍的变化压缩到几十 dB 以内,便于显示与比较。
转成加法关系
多级增益或衰减的乘法关系,在 dB 下会变成加法:
L_{\rm 总} = L_1 + L_2 + \cdots这类似于归一化后“相加”的感觉,但本质还是比值的对数。
无量纲比值
分贝只是一个比值单位,表示“这里比那里大多少倍(的对数)”,而非把数值映射到固定区间(如 0–1)内。
词汇表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

